
Ответы на экзаменационные вопросы по физике / 20better
.docПространственное квантование. Опыт Штерна - Герлаха. Гипотеза Гаудсмита - Уленбека. Спин электрона.
В
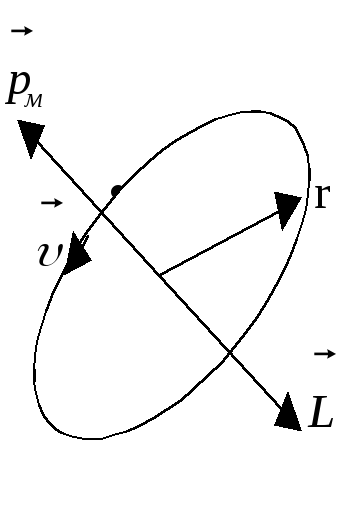
![]() электрона и пропорциональный ему
магнитный момент
электрона и пропорциональный ему
магнитный момент
![]() :
:
![]() ;
L
= mr;
;
L
= mr;
![]() ориентированы перпендикулярно плоскости
орбиты электрона и направлены в
противоположные стороны вследствие
отрицательного знака заряда электрона:
ориентированы перпендикулярно плоскости
орбиты электрона и направлены в
противоположные стороны вследствие
отрицательного знака заряда электрона:
![]() ,
где
,
где
![]() - орбитальное гиромагнитное отношение
для электрона (вектор
- орбитальное гиромагнитное отношение
для электрона (вектор
![]() направлен согласно правилу правого
винта (буравчика)).
направлен согласно правилу правого
винта (буравчика)).
В отличие от теории
Бора, в квантовой механике орбит нет, и
для указания ориентации векторов
![]() и
и
![]() должно быть выбрано некоторое направление
Z в пространстве. Обычно это направление
внешнего магнитного поля (либо направление
внутреннего магнитного поля всех
электронов атома кроме данного, а также
и ядра атома), и расположение
должно быть выбрано некоторое направление
Z в пространстве. Обычно это направление
внешнего магнитного поля (либо направление
внутреннего магнитного поля всех
электронов атома кроме данного, а также
и ядра атома), и расположение
![]() задается углом наклона к оси Z.
задается углом наклона к оси Z.
В
![]() относительно избранного направления
внешнего магнитного поля могла быть
любой (плоскость орбиты могла произвольным
образом ориентироваться относительно
внешнего или внутреннего магнитного
поля). В квантовой механике выявилось
наличие неклассического эффекта,
названного пространственным
квантованием, согласно
которому орбитальный момент импульса
электрона может иметь лишь такие
ориентации в пространстве, при которых
проекция момента импульса на данное
направление Z принимает значения, кратные
постоянной Планка
относительно избранного направления
внешнего магнитного поля могла быть
любой (плоскость орбиты могла произвольным
образом ориентироваться относительно
внешнего или внутреннего магнитного
поля). В квантовой механике выявилось
наличие неклассического эффекта,
названного пространственным
квантованием, согласно
которому орбитальный момент импульса
электрона может иметь лишь такие
ориентации в пространстве, при которых
проекция момента импульса на данное
направление Z принимает значения, кратные
постоянной Планка
![]() .
Этот результат впервые был получен как
следствие обобщенных Зоммерфельдом
правил квантования боровских орбит. В
квантовой механике строго доказывается,
что Lz =
m
.
Этот результат впервые был получен как
следствие обобщенных Зоммерфельдом
правил квантования боровских орбит. В
квантовой механике строго доказывается,
что Lz =
m![]() ,
где m = 0,
1,
2, ….
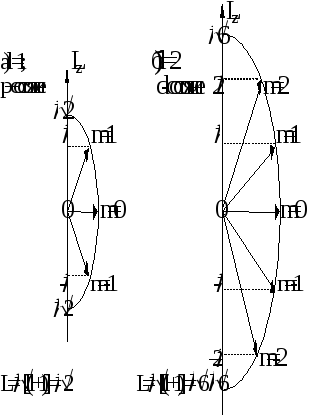
l. На рис.
приведены возможные ориентации вектора
,
где m = 0,
1,
2, ….
l. На рис.
приведены возможные ориентации вектора
![]() в пространстве для p и d состояний (l
= 1 и l = 2):
в пространстве для p и d состояний (l
= 1 и l = 2):
В
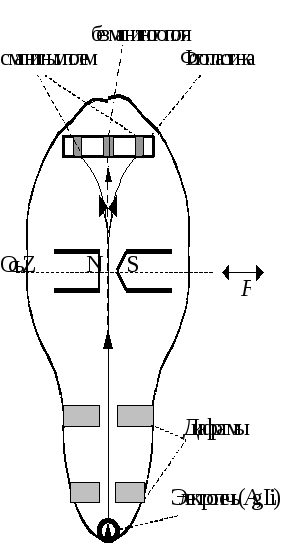
![]() ,
которая и вызывает отклонение пучка
атомов от их положения в случае отсутствия
неоднородного внешнего магнитного
поля. Но тот факт, что включение магнитного
поля приводило к расщеплению пучка на
два, говорил о наличии двух возможных
ориентаций магнитных моментов атомов
относительно направления внешнего
магнитного поля.
,
которая и вызывает отклонение пучка
атомов от их положения в случае отсутствия
неоднородного внешнего магнитного
поля. Но тот факт, что включение магнитного
поля приводило к расщеплению пучка на
два, говорил о наличии двух возможных
ориентаций магнитных моментов атомов
относительно направления внешнего
магнитного поля.
По квантовой
механике механический момент импульса
равен L =
![]() √[l(l
+ 1)] и связанный с ним магнитный момент
√[l(l
+ 1)] и связанный с ним магнитный момент
![]() ,
где
,
где
![]() - магнетон Бора – своего рода единица,
квант магнитного момента, точнее его
проекции: рмz
= Бm,
где m = 0,
1,
2, …
l.
- магнетон Бора – своего рода единица,
квант магнитного момента, точнее его
проекции: рмz
= Бm,
где m = 0,
1,
2, …
l.
Для серебра Штерн
и Герлах получили значение
![]() порядка Б.
Но у элементов первой группы таблицы
Менделеева, к которым относится серебро,
в основном состоянии атом имеет значение
l
= 0 (электрон находится в S - состоянии)
и, соответственно, нулевое значение
момента импульса L =
порядка Б.
Но у элементов первой группы таблицы
Менделеева, к которым относится серебро,
в основном состоянии атом имеет значение
l
= 0 (электрон находится в S - состоянии)
и, соответственно, нулевое значение
момента импульса L =
![]() √[l(l
+ 1)]. Поэтому возникает серьезный вопрос
об истолковании результатов опыта
Штерна и Герлаха. Подобная же ситуация
сложилась и при наблюдении спектров
щелочных металлов, которые также носили
дублетный характер, то есть спектральные
линии в них расщеплялись на две близко
расположенные линии, разнос которых
также зависел от величины неоднородного
внешнего магнитного поля. К тому же в
опытах Эйнштейна и Гааза обнаружилось
аномальное значение гиромагнитного
соотношения для ферромагнетиков, в два
раза различающееся с выше приведенным.
Все эти несоответствия были устранены
в 1925 г Гаудсмитом и Уленбеком путем
предположения о наличии у электрона
наряду с орбитальным, еще и собственного
момента импульса, названного спиновым,
или, коротко - спином (спин - с английского
- волчок, веретено). Позже Дираку удалось
поставить эту гипотезу на теоретическую
основу, выведя спин из полученного им
релятивистского уравнения квантовой
механики.
√[l(l
+ 1)]. Поэтому возникает серьезный вопрос
об истолковании результатов опыта
Штерна и Герлаха. Подобная же ситуация
сложилась и при наблюдении спектров
щелочных металлов, которые также носили
дублетный характер, то есть спектральные
линии в них расщеплялись на две близко
расположенные линии, разнос которых
также зависел от величины неоднородного
внешнего магнитного поля. К тому же в
опытах Эйнштейна и Гааза обнаружилось
аномальное значение гиромагнитного
соотношения для ферромагнетиков, в два
раза различающееся с выше приведенным.
Все эти несоответствия были устранены
в 1925 г Гаудсмитом и Уленбеком путем
предположения о наличии у электрона
наряду с орбитальным, еще и собственного
момента импульса, названного спиновым,
или, коротко - спином (спин - с английского
- волчок, веретено). Позже Дираку удалось
поставить эту гипотезу на теоретическую
основу, выведя спин из полученного им
релятивистского уравнения квантовой
механики.
Значение спинового момента выражается через четвертое, спиновое квантовое число s:
![]() .
Проекция
.
Проекция
![]() должна быть квантована и иметь 2s + 1
ориентаций. Из опытов Штерна и Герлаха
вытекало, что атома серебра таких
ориентаций две, то есть 2s + 1 = 2
s = ½; Ls
=
должна быть квантована и иметь 2s + 1
ориентаций. Из опытов Штерна и Герлаха
вытекало, что атома серебра таких
ориентаций две, то есть 2s + 1 = 2
s = ½; Ls
=
![]() [½(½
+ 1)] = -
[½(½
+ 1)] = -![]() 3/2;
Lsz
=
s
3/2;
Lsz
=
s![]() =
= ![]() /2.
Или Lsz
=
/2.
Или Lsz
= ![]() /2
= ms
/2
= ms![]() ,
где ms
=
½.
,
где ms
=
½.
Для атомов первой
группы момент импульса равен спину
валентного электрона. Связанный с
механическим магнитный момент электрона
равен:
![]() ;
;
![]() и
и
![]() ;
;
![]() .
.
Спиновое гиромагнитное отношение (отношение магнитного момента к механическому) у электрона оказывается в два раза выше орбитального, что и объясняет результаты опытов Эйнштейна и де Гааза для ферромагнетиков, ибо ферромагнетизм - эффект спиновый.
