Ответы на экзаменационные вопросы по физике / 13

Общее (нестационарное) уравнение Шредингера

Состояние движения микрообъекта задается не координатами и импульсами, не траекторией, как в макромире, а некоторой функцией координат и времени, носящей в общем случае комплексный и волновой характер. В микромире обнаружился более общий, статистический характер детерминизма, причинности. Однозначные детерминизм и причинность классической механики, адекватные движениям макрообъектов, оказались лишь огрубленным приближением. Вероятностный детерминизм в поведении микрообъектов проявляется в наличии некоторого уравнения, связывающего заданными взаимодействиями (граничными условиями) начальную и будущую волновые функции. Это уравнение, найденное Шредингером и получившее его имя, является исходным, фундаментальным уравнением квантовой механики, подобно уравнению 2 - ого закона Ньютона для классической механики. В рамках квантовой механики оно ниоткуда не выводится, а его справедливость подтверждается всей совокупностью его следствий, сопоставляемых с опытными фактами. Решением этого уравнения и является функция состояния движения квантового объекта - волновая функция. Поясним вид этого уравнения в простейшем одномерном случае, на примере свободной частицы, движущейся вправо вдоль оси х. Вид волновой функции такой частицы известен - это плоская волна де Бройля . Для свободной частицы потенциальная функция (энергия) U равна нулю, и полная энергия Е равна кинетической энергии: E = T + U = Т = m²/2 = р²/2m (p = m). Т. к. E ~ , то легко выявляется инвариантная дифференциальная взаимосвязь и образующая собой квантовое уравнение движения частицы. Для этого надо взять частную производную от волновой функции по времени, которая фактически сведется к умножению ее на энергию Е:

; 

и затем два раза продифференцировать волновую функцию по координате; при этом у волновой функции появится множитель р². А затем, используя связь Е = р²/2m, можно связать первую производную от волновой функции по времени и вторую производную по координате. Эта взаимосвязь и будет представлять собой искомое дифференциальное уравнение для волновой функции свободной частицы, т. е. уравнение Шредингера:

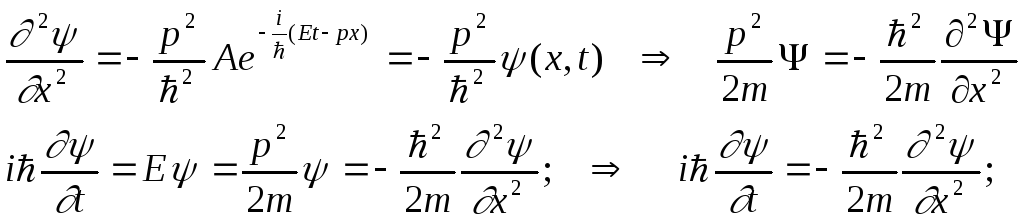
В общем случае, для частицы, движущейся в силовом поле, задаваемом потенциальной энергией, точнее, потенциальной функцией U(х, t), полная энергия Е частицы будет равна сумме , и уравнение Шредингера, называемое общим или временным, примет вид: или в 3-х мерном случае:

где - оператор Лапласа, представляющий собой сумму вторых частных производных по пространственным координатам.

Уравнение Шредингера позволяет однозначно находить волновую функцию по известным начальным [] и граничным {U(x, y, z, t)} условиям и в этом смысле оно определяет динамически закономерную связь состояний движения квантового объекта. Напомним, что волновая функция, через квадрат своего модуля задает, определяет плотность вероятности нахождения частицы в данном месте в данный момент времени, а это есть функция статистического распределения.

Волновая функция подчиняется так называемым стандартным или естественным условиям (фактически условиям физической реализуемости). К ним относят следующие условия:

1. Непрерывность. Разрывы волновой функции будут означать и наличие разрывов квадрата ее модуля, за которыми стоят разрывы плотности вероятности и самой вероятности нахождения частицы в том или ином месте. А это означает эффекты рождения или уничтожения частиц, с чем обычная квантовая механика непосредственно дела не имеет.

2. Однозначность. В случае неоднозначности волновой функции не может реализоваться принцип детерминизма и предсказуемости квантовомеханического состояния объекта, а с ними и суть научности в отображении природы.

3. Гладкость. (дифференцируемость) означает конечность и непрерывность первых производных волновой функции. Это требование связано с тем, что уравнение Шредингера содержит вторые производные от  - функции, которые для негладкой функции будут принимать бесконечные значения.

4. Конечность. При наличии бесконечных значений волновой функции ее невозможно отнормировать и применить понятие самой вероятности.

Уравнение Шредингера ограничивает квантовомеханический анализ случаем малых скоростей (медленных движений), т. е. является основой нерелятивистской квантовой теории и не учитывает четвертую (спиновую) степень свободы микрообъекта. В 1929 г. Дирак получил для электрона более общее уравнение, учитывающее спин и являющееся релятивистским. Его анализ выходит за рамки нашего курса.

Стационарные состояния и уравнение Шредингера для стационарных состояний

Частным, но важным для практики случаем состояния движения микрообъектов, является случай так называемых стационарных состояний, при которых силовая функция U(x, y, z, t) = U(x, y, z) - не зависит от времени и приобретает смысл потенциальной энергии. Соответственно, полная энергия системы (система консервативна) точно определяется, ибо можно реализовать при t  , Е  0.

В стационарном состоянии распределение вероятностей местонахождения частицы (плотность вероятности) должна оставаться постоянным во времени, то есть . Отсюда следует, что волновую функцию в стационарном состоянии можно представить в виде произведения:

. Здесь зависимость (t) носит гармонический характер, и

= const.

Примером волновой функции в стационарном состоянии является плоская волна де Бройля, описывающая состояние движения свободной частицы, для которой U(x, y, z) = const = 0. Для свободной частицы сохраняется (остается неизменным) импульс, и для нее - в волновой функции разделяются множители: пространственный (х, у, z), играющий роль амплитуды волновой функции, и временной , определяющий гармонический характер изменения волновой функции во времени.

Подставив волновую функцию в виде плоской волны де Бройля в общее, временное уравнение Шредингера, получим после сокращений уравнение Шредингера для стационарных состояний:

Полученное уравнение называют еще стационарным уравнением Шредингера или уравнением Шредингера не зависящим от времени