Ответы на экзаменационные вопросы по физике / 16

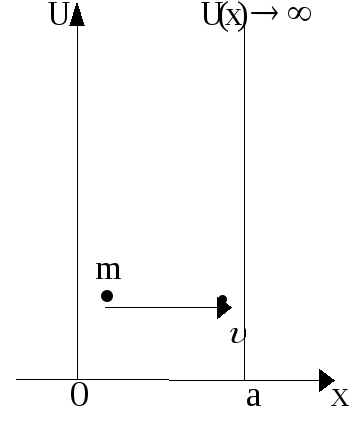
2. Частица в одномерной прямоугольной "потенциальной яме".

Р

ассмотрим вначале идеализированную потенциальную яму с бесконечно высокими стенками, называемую потенциальным ящиком. Потенциальный ящик задается рельефом, который аналитически и графически предстает в следующем виде: 0 при 0  х  а

U(х) =

• при х  0 и х  а

где а - ширина ямы (ящика).

Внутри ящика потенциальная энергия частицы равна нулю, а вне его - бесконечности, поэтому частица, помещенная в ящик, выйти из него не сможет. Это соответствует условию (х) = 0 при и .

Уравнение Шредингера для стационарных состояний применяем только для области , т. е. внутри ящика, где потенциальная энергия равна нулю. Вне ящика , то есть, частицы там нет. Итак, при U = 0: , где k = (2mЕ/²) - волновое число. Определим решение этого уравнения для частицы в ящике. Оно подобно рассмотренному ранее для случая свободной частицы. Но здесь появляются граничные условия (определяемые потенциальным рельефом U (х)), накладываемые на волновую функцию: (0) = 0 и (а) = 0.

В ящике движение частицы является ограниченным, и волновая функция частицы не может выражаться бегущей волной. Вернее, здесь надо брать суперпозицию двух бегущих в противоположные стороны волн, которые в итоге дают стоячую волну .

Из граничного условия (0) = 0 следует: (0) = В = 0 и тогда . Из условия на другой границе (а) = 0  (а) = А sin kа = 0  kа = n, где n = 1, 2, 3, … Отсюда и проистекает квантование волнового числа k = n/а, а с ним и импульса р = k, и энергии Е частицы в ящике:

. Эта формула выражает спектр собственных значений энергии частицы в ящике.

Квантование энергии является результатом ограничения (локализации) движения микрочастицы. Условие k = n/а есть условие «стоячести» волны де Бройля частицы в ящике, при котором на длине (ширине) а ящика должно укладываться целое число n полуволн /2 волновой функции частицы: k = 2/ = n/а  а = n/2.

Расстояние между соседними энергетическими уровнями частицы в ящике равно:

В

отличие от атома водорода, в потенциальном ящике энергетические уровни не сгущаются с ростом их номера n, а разрежаются.

Разность между соседними энергетическими уровнями обратно пропорциональна массе частицы и квадрату ширины ящика: Е_n  1/m и Е_n  1/а².Таким образом, квантовый характер энергетического спектра движущейся частицы усиливается с уменьшением ее массы и с локализованностью (ограниченностью в пространстве) ее движения (с уменьшением а).

Относительное расстояние между энергетическими уровнями Е_n/Е_n = (2n + 1)/n²  1/n убывает с ростом номера энергетического уровня. При больших значениях квантового числа n, определяющего номер и величину энергетического уровня, дискретность энергии нивелируется (энергия уровня растет быстрее, чем интервал между ними). Это означает фактически переход к классической физике; здесь "работает" принцип соответствия - при больших квантовых числах эффекты квантования нивелируются, и движение приобретает классические черты, отражаемые классической механикой. Квантованность нивелируется и при а  . Спектр энергии частицы становится при этом непрерывным, что соответствует переходу к свободной частице.

Волновая функция частицы в ящике оказывается различной на разных энергетических уровнях. Множитель А определяется из условия нормировки:

и

n = 1;

n = 2;

n = 3;

На длине (ширине) ящика а укладывается целое число длин полуволн - функции (условие "стоячести" волны).

В

нижнем энергетическом состоянии (n = 1), называемом основным, частица с большей вероятностью находится в центре ящика. При n = 2, наоборот, частица в центре ящика находиться не может, ибо там плотность вероятности |(а/2)|² = 0.

С ростом квантового числа n возрастает число равновероятных мест пребывания частицы в ящике. При n   волновая функция осциллирует столь часто, что максимумы практически сливаются, и частица равновероятно находится в любой точке ящика¹: имеем, согласно принципу соответствия, переход от квантовой к классической механике.

1 Все меняется столь часто, что практически ничего не меняется.