7. Моделирование дискретных каналов

Статистическое моделирование ДК заключается в разработке алгоритма/модуля, воспроизводящего определенную математическую модель канала и формирующего соответствующие этой модели последовательности ошибок/искаженных блоков. На основе общих положений о генерации случайных последовательностей, подчиненных заданному закону, в модуле-имитаторе ДК первичным генератором случайных последовательностей является датчик случайных чисел, равномерно распределенных в интервале [0,1]. Базовый датчик должен иметь достаточно большой период, чтобы не порождать дополнительных ограничений на время моделирования, и не должен вносить дополнительную корреляцию в формируемые последовательности. Последовательность чисел, генерируемая первичным датчиком, преобразуется согласно математическому описанию канала в двоичную последовательность ошибок или искаженных блоков В зависимости от способа представления двоичных последовательностей и их статистического описания можно наметить два основных подхода к построению моделирующего алгоритма.

При символьном представлении реализаций двоичной последовательности или , например:

0100111000100001 ... .

осуществляется моделирование отдельных символов последовательности, что требует проигрывания каждого символа 0/1 с использованием одного или нескольких случайных чисел.

Для каналов без памяти (с независимыми ошибками) независимым случайным событием является результат приема отдельного символа /блока, представляемый случайной величиной

Основной параметр такого случайного процесса - число ошибок k на интервале длины n подчиняется биномиальному распределению: .

Рис. 3. Биномиальное распределение (схема моделирования)

Поскольку для равномерно распределенной случайной величины z вероятность попадания на отрезок [0,p) равна p, а на отрезок [p,1) - соответственно q, то будем считать, что случайная величина x принимает значение 1, если случайная величина z попала на отрезок [0,p), и значение 0 - если z попала на отрезок [p,1), т.е. будем фиксировать значение x=1, если датчик выработал число z<p, и значение x=0 в противном случае (рис. 3).

При наличии памяти в канале генерируемая последовательность ошибок/искаженных блоков может быть рассмотрена как простая цепь Маркова с двумя состояниями: S₀=0 - правильный прием, S₁=1- ошибка в символе/блоке. Описание случайного процесса или в этом случае осуществляется посредством задания/расчета переходных вероятностей p_ij=p(s_j/s_i) и вероятностей начальных состояний P₀,P₁.

Согласно этому описанию необходимо сначала разыграть начальное состояние, сравнив случайную величину z с начальными вероятностями P₀/P₁. Моделирование каждого следующего состояния определяется тем, какое из состояний ему предшествовало: очередная случайная величина z сравнивается либо с переходными вероятностями p₀₀/p₀₁, если предшествовало - S₀, либо с p₁₁/p₁₀, если предшествовало - S₁ (рис. 4).

В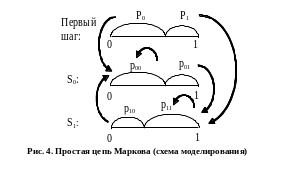 более общем случае марковской модели канала (схема М), когда цепью Маркова описывается последовательность состояний канала, а последовательность ошибок является функций марковской цепи, определяемой вектором условных вероятностей ошибок в каждом состоянии, имитационной модуль канала должен формировать два взаимосвязных вероятностных процесса: последовательность состояний и последовательность ошибок . После генерации очередного состояния S_i необходимо выяснить, будет ли соответствующий ему символ принят безошибочно или с ошибкой. Поскольку каждое такое выяснение, каждый розыгрыш состояния, символа, блока связан с генерацией отдельного случайного числа, то при подобном подходе требуются весьма существенные затраты машинного времени.

Более компактным и более эффективным с точки зрения моделирования является интервальное представление двоичных последовательностей, когда задаются вероятностные распределения не для самих символов 0/1, а для длин их серий или интервалов между ними. Для реализации таких представлений в моделирующих алгоритмах целесообразно использовать модели ошибок, основанные на процессах восстановления, схема B.

Для моделей с мгновенным восстановлением, когда задается функция распределения F(₀)=1-R(₀) длин ₀ безошибочных интервалов, где R(₀)=P(₀₀) - кумулятивная функция распределения, моделирующий алгоритм представляет собой генератор псевдослучайных чисел, имитирующий заданный закон распределения случайной величины ₀=0,1,2..., например, рассмотренная ранее двоичная последовательность запишется в виде:

.

Алгоритм реализующий такой генератор, может быть основан на использовании метода обратных функций путем решения относительно ₀ уравнения z=R(₀):

₀=R^-1(z),

где z - случайная величина, равномерно распределенная на интервале [0,1]; R^-1(z) - функция, обратная кумулятивной функции:

Используя первичный датчик случайных чисел z и полученное соотношение для ₀ , можно формировать в интервальном представлении различные реализации последовательности ошибок, отвечающие заданному распределению.

Для моделей с конечным временем восстановления, в которых последовательность ошибок представляется в виде последовательности пакетов ошибок, где возникают независимые ошибки с вероятностью ₁, и промежутков между пакетами, где вероятность ошибки мала ₀<<₁ и задаются функции распределения F(l) длин l=1,2, ... пакетов и F() длин =1,2 ... промежутков, может быть использована следующая методика моделирования. С помощью первичного датчика случайных чисел z разыгрывают величину первого промежутка/пакета. Затем моделируют последовательность ошибок в пределах этого промежутка/пакета, разыгрывая интервалы ₀ между соседними ошибками, которые в этих пределах распределены по геометрическому закону с параметром ₀/₁. Процесс моделирования ошибок будет закончен, когда очередная ошибка окажется вне промежутка/пакета. Далее переходят к моделированию следующего пакета/промежутка.

Для марковских моделей канала, совмещающих в себе два вероятностных процесса: чередование состояний канала и возникновение ошибок в текущем состоянии, с целью достижения наибольшего быстродействия оба процесса можно моделировать интервально, определяя случайным образом длины и номера состояний канала и промежутки между ошибками в каждом состоянии. Длительность l_i пребывания канала в i-ом состоянии, измеряемая числом символов, передаваемых во время этого состояния, вычисляется по формуле

l_i=[lnz/lnp_ii]+1,

где p_ii - условная вероятность сохранения i-го состояния при передаче очередного символа; z - случайное число, получаемое от первичного датчика. Промежутки между ошибками в i-ом состоянии, распределенные по геометрическому закону, определяются выражением

₀=[lnz/ln(1-_i)],

где _i - вероятность ошибки в i-ом состоянии. Выбор следующего состояния производится путем сравнения случайного числа z со значениями безусловных вероятностей состояний.

Таким образом, можно осуществлять моделирование различных распределений ошибок в дискретном канале на первом или втором уровне его описания (символьном или блочном), используя одну из схем представления двоичных последовательностей (символьную или интервальную). Иногда удобно пользоваться комбинированным интервально-символьным представлением (например, для модели Беннета-Фройлиха).