8)Принципы, лежащие в основе классической логики. Основные разделы неклассической логики.

1)Принцип двузначности.Слабая формулировка – всякое высказывание имеет в точности одно из 2-ух значений – и или л.

1 .1.Принцип двузначности в сильной формулировке: Возможными значениями высказываний являются лишь абстрактные объекты и и л. 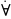А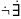 х(f(A)=x&x {и,л})

f(A) – ф-ция значения. А х(f(A)=х х {и,л}).

1.2.Принцип всюдуопределенности. Высказывание принимает по крайней мере одно значение из множества {и,л}. А(f(A)=и или f(A)=л) или А(f(A)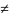 л f(A)=и)

1.3. Принцип запрета пресыщенных оценок: высказывание принимает не более одного значения из множества {и,л}. А(f(A)=и и f(A)=л) или А(f(A)=и f(A) л)

Обобщенный принцип: А(f(A)=и f(A) л) – т.е нам достаточно задать только условия истинности высказываний.Если отказываемся от этого принципа, то получаем многозначную логику, одна из многозначных логик – логика Лукасевича.

2)принцип экстенсиональности(композициональности). Значение сложного выражения зависит только от значений составляющих его выражений. Смыслы знаков или иные синтаксические, семантические и прагматические их характеристики могут в данном случае вовсе не приниматься во внимание. При построении систем классической логики принцип экстенсиональности, в отличие от принципа двузначности, не всегда постулируется явным образом. Тем не менее его действие проявляется в наличии в классич. логике логических законов замены равного равным и замены эквивалентного эквивалентным. Замена равного равным – t₁ =t₂ (A(t₁) A(t₂)). A(t₂) -ф-ла, получающаяся в рез-те замены некоторого числа вхождений терма t₁ в ф-лу A(t₁) на терм t₂.Если отказываемся от этого принципа, то получаем модальную, релевантную логику.

3)Классическая(корреспондентная )трактовка истинности. Восходит к трудам Аристотеля. Принадлежит А.Татскому. Высказывание истинно если и только если то, что в нем утверждается, имеет место в действительности. Тр(р истина) = «р» - имеет место в реальности. Не работает при высказываниях о будущем.Если отказываемся от этого принципа, то получаем интуиционистскую логику.

4)Экзистенциальные предпосылки(о непустоте). Область интерпретации(универсум рассмотрения) содержит, по крайней мере, 1 объект. Если отказываемся от этого принципа, то приходим к свободным логикам и можем рассматривать несуществующие объекты.

Отказ от одного или нескольких принципов позволяет построить ту или иную неклассическую логику.

9)Проблема будущих случайных событий и логика Лукасевича.

Аргумент лог. фатализма:

1)(р-истинно)˅(р-ложно) – высказывание о том, что событие S произойдет или не произойдет.

2) S – случайное событие.

3) р-истинно S неизбежно произойдет.

4)р-ложно S неизбежно не произойдет.

5) S - неизбежно произойдет˅ S - неизбежно не произойдет – из 1,2,3,4 по конструктивной дилемме.

6)¬ S – случайное.

Отсюда делается вывод, что случайных событий нет. Но Аристотель делает вывод, что принцип двузначности для будущих событий не действует.

7)¬( (р-истинно)˅(р-ложно)) - ¬в:2,6, т.е высказывания о случайных будущих событиях нельзя оценить как истинные или ложные. Лукасевич предлагает неведущий к фатализму принцип: всякое высказывание либо истинно, либо ложно, либо случайно. Предложил значение «случайно» - р¬(р-истинно)&¬(р-ложно).р-и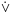 р-л р –сл. – тогда принцип трехзначности. {1,1/2,0}. При классических аргументах 1 и 0 ф-лы должны принимать в многозначной логике те же самые значения, что и в классической двузначной логике. Это нормальная логика. Нормальные многозначные логики – если в логике есть аналоги классической логики, то связки ведут себя также как в классической логике. Ненормальные(нерегулярные) логики – значения ведут себя по-другому, не как в классической логике.3ⁿ – кол-во строк в таблице в лог. Лукасевича. Ф-ла А общезначима в 3-ех значной логике Лукасевича, тогда и только тогда когда она принимает значение 1, на любых наборах значений пропозициональных переменных, входящих в нее. Гǀ=В – из множества ф-л Г в 3-ех значной логике Лукасевича логически следует В, тогда и только тогда, когда ф-ла В принимает значение 1 на всех тех наборах пропозициональных переменных, на которых все ф-лы из Г принимают значение 1(определение через сохранность значения). А_1….А_nǀ=B

1 1 ½

ǀ =p˅¬p – не является законом логики Лукасевича. ǀ=¬ (р&¬р). Не все законы классической логики являются законами логики Лукасевича. Не работают законы выражения одних связок через другие. Лог. Лукасевича не является функционально полной, т.к связок ¬ и логики Лукасевича недостаточно, чтобы выразить любую ф-цию, заданную на множестве из 3-ех истинностных оценок {1,1/2,0}. A˅B (A B) B. Если логика не функционально-полная, то мы можем добавлять связки - ^*.

А *В (А (А В)). Если добавить оператор Слупецкого, то логика станет функционально полной – Т ставит под сомнение А. АТА

1 ½

½ ½

0 ½

Определение значений ф-л в логике Лукасевича: |A&B|=min(|A|,|B|); |A˅B|=max(|A|,|B|); |A B|=min(1,1-|A|+|B|).

Вайсберг предложил аксиомы логики Лукасевича.