17)Первоуровневая релевантная логика: сис-ма fde, аналитико-табличное построение.

Материальная неадекватно формализает условную связь, потому что значения ф-лы p q полностью определяются значениями антецедента и консеквента. Это приводит к несоответствию между смыслом союза если…то естественного языка и материальной импликацией.Материальная импликация обладает целым рядом свойств, не совпадающих с нашей интуицией, и в этом смысле она является парадоксальной. Эта парадоксальность распространяется также и на классическое понятие лог. следования, т.к предложения о лог. следовании тесно связаны с импликативными предложениями посредством соотношения: Аǀ=В ǀ=А В. В классической логике легко воспроизводятся несоответствующие нашей интуиции утверждения о лог. следовании? из противоречия логически следует все что угодно и тавтология логически следует из чего угодно

Парадоксы следования:

1)А&¬Аǀ=В

2)Вǀ=А˅¬А

парадоксы импликации:

3) ǀ= ¬В (В А)

4) ǀ= В (А В)

Аǀ= В ǀ= А В(связывает парадоксы 1-4). Согласно нашей интуиции неадекватно формализует импликативную связь. (А В)-говорит о связи между фактами (¬А˅В) – говорит только о фактах. Льюису не удалось предотвратить парадоксы

Правила вывода:

R 1:A˫B,A˫C R2:A˫B, C˫B R3:А˫В,В˫С R4:A˫B

A˫B&C A˅C˫B А˫С ¬B˫¬A

П равила для аналит.таблиц.2 отрицания - ¬ и ТА-не и, FA-не л.

Г , Т(А&В), [&] Г,F(A&B), [¬&]

Г,ТА,ТВ, Г, FA, Г,FB,

Г ,T(A&B), Г,F(A&B), Г,T(A˅B),

Г ,TA, Г,TB, Г,FA,FB, Г,TA, Г,TB,

Г ,F(A˅B),

Г,FA, Г,FB, Г,T¬A, Г,F¬A,

Г,FA, Г,TA,

Г ,T¬A, Г,F¬A,

Г,FA, Г,TA, всего 12 правил(т.е+2 правила для˅).

Т аблица замкнута, если на последней строке таблицы ф-лы вида – TC,TC или FC,FC

18)Понятие описания состояния, семантика обобщенных описаний состояний и информационная трактовка следования в релевантной логике.

Первая сис-ма релевантной логики построена Орловым(1928). В 1943 Клини построил релевантную логику(как у Орлова, т.к переводил работу Орлова). информационная трактовка следования в релевантной логике: В1956 году вышла статья Аккермана, он построил первую синтаксическую сис-му релевантной логики(А влечет В, если А информативнее чем В). До 70-х годов эти сис-мы существовали без семантик. Аккерман - Аǀ=В – информация В составляет часть информации А.Е.К Войшвилло – выражение логического содержания через информацию. Карнап – информация как мера ограничения исходного множества.

Исходное множество возможностей (М) – это мн-во всех приписываний значений ф-лам р&q и р, т.е мн-во строк в таблице истинности.

	р	q	р&q	р
1	И	И	и	и
2	И	Л	л	И
3	Л	И	Л	Л
4	л	л	л	л

2,3,4 1

множество М.ограничили мн-во М.
Информация произвольной ф-лы А относительно некоторого М понимается как мера ограничения мн-ва М, принятием ф-ла А за истину. Информация – I(A,M).

p &qǀ=p I(p,M) составляет информацию I(p&q, M) Mp&q Mp.

Aǀ=B M_A M_B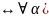 α)

M_A – результат ограничения исходного мн-ва возможностей. M_A={α:TA/α}

Семантика FDE:

Tp/α p α

Fp/α ¬ p α

T p/α p α

Fp/α ¬ p α

T(A&B)/α TA/α и ТВ/α; F(A&B)/α FA/α или FВ/α; Т(А˅В)/α TA/α или ТВ/α

F(A˅B)/α FA/α и FВ/α; Т¬А/α FA/α; F¬A/α TA/α

В системе нет вообще.

Пусть L – множество пропозициональных переменных и их отрицаний – L={p,¬p,q,¬q……r_n,¬r_n……}- т.е множество произвольных переменных. Описание состояния(α) есть произвольное подмножество L, удовлетворяющее следующим условиям:

1) р¬(р и ¬р ) – непротиворечивость.

2) р(р или ¬р ) – условие непустоты.

Примеры: {p,q}, {p,¬q},{¬p,q}- такие множества – это описания состояния. Это классическое описание состояния.Обобщенное описание состояния – это произвольное подмножество L(допускаются наряду со старыми описаниями состояния, описания и другого сорта – неполные и противоречивые) – {p,¬p},

p &¬pǀ=q док-во:

1)Т(р&¬р)/α

2 )Тq/α

3)Tp/α и Т¬р/α – из 1.

4)р α и ¬р α - из 3.

5 ) q α - из 2

Опровергающий пример: {p,¬p,¬q}

q ǀ=p˅¬p – т.к могут быть описания состояния.Описания состояния – это карнаповская идея, ее попытались использовать. Если мы хотим адекватно формализавать лог. связь, нас карнаповский механизм не устраивает, нам нужны обощенные описания состояния.