Ответы на логику.

2 Курс 3 семестр.

1)Понятие как форма мысли. Выражение понятий в языке. Логическая форма понятия. Объем и содержание понятия.

Понятие можно назвать особой ментальной конструкцией. Понятие – это мысль, в которой на основании наличия у предметов некоторого признака, эти предметы выделяются из исходного множества и собираются в класс. Понятие в языке выражается как αА(α) – предмет α из множества U, такой что А. У любого понятия 2 характеристики – объем(множество предметов), содержание(признак, на основании которого предметы выделяются из исходного множества). Объем понятия – класс предметов, обладающих признаком, зафиксированном в содержании понятия. Отдельный объект, принадлежащий объему понятия и обладающий признаком, зафиксированном в содержании понятия называется элементом объема понятия(например – понятие библиотека, тогда элемент объема – библиотека №1). Универсум – это исходное множество, из которого выбираются элементы в понятии. В качестве универсума выбирается ближайший род понятия. Если у 2-ух понятий совпало содержание, то и объемы у них одинаковые. Языковая форма понятия(2 способа ее задания):

1)понятийные конструкции(универсалии. Пример – четырехугольник, имеющий равные стороны и прямые углы.

2)описательные термины – как сокращения для понятийных конструкций. Пример – квадрат.

α может быть:

1)предметная переменная(x,y,z).

2)предметно-функциональная переменная(f ⁿ,gⁿ)

3)предикаторная переменная(Pⁿ)

α может пробегать по:

1)множествам – {x}

2)последовательностям < x,y>.

Если αА(α) – логическая форма понятия, то ф-ла А(α) представляет логическое содержание данного понятия, а результат интерпретации этой формулы будет представлять фактическое содержание понятия. Пример – Q²(x,a) – лог.содержание, фактическое содержание – чел., который старше Маркина. Фактический объем – множество предметов, обладающих признаком, зафиксированным в фактическом содержании понятия. Логич. объем – множество абстрактных предметов из неинтерпретируемого универсума, обладающих признаком, зафиксированном в логическом содержании.

2)Закон обратного отношения между содержаниями и объемами понятий. Обобщение и ограничение понятий.

Закон обратного отношения между объемами и содержаниями понятий – если и только если одно непустое и неуниверсальное понятие по объему включается в другое непустое и неуниверсальное понятие, то содержание 1-ого понятия информативнее содержания второго понятия(т.е следует). Для того чтобы сравнивать понятие есть логическое следование. Если первое понятие - p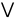 q и 2-ое – р, то р ǀ= p q.

Ограничить непустое понятие αВ(α) – это значит перейти к понятию αА(α), такому что wαA(α) wαB(α) – это понятие по объему включается в первое. Операция обобщения – это операция, обратная операции ограничения. Обобщить непустое понятие αВ(α) – это значит перейти к понятию αА(α), такому что wαB(α) wαA(α) это понятие включает первое.Обобщать и органичивать можно только непустые понятия. Предел операции органичения – это единичное понятие. Предел операции обобщения – универсальное понятие. Результатом этой операции всегда является понятие. Чтобы ограничивать, нужно навешивать доп. признаки.