4. Определение напряжения в конце передачи
Для определения напряжение в конце передачи рассматривается уравнение четырехполюсника:
, (4.1)
где
и
— приведенные к высшей (входной) стороне
напряжение и ток в конце передачи.
Напряжение
в начале передачи задано по абсолютной
величине как в максимальном, так и в
минимальном режимах. Приведенное
приближенное значение тока
обеих цепей можно определить по
номинальному напряжению высшей стороны
и заданной мощности нагрузки:
. (4.2)
Известен
также угол между
и
,
который является углом сопротивления
нагрузки на шинах С (рис. 8), т. е.:
. (4.3)
Обобщенные
постоянные
и
передачи по величине и фазе были
определены при решении п. 3.3. Таким
образом, в уравнении четырехполюсника
неизвестны напряжение в конце линии
по величине и углу, а также угол между
и
.
Эта задача может быть решена графически:
1) направляем ток по вещественной оси;
2)
определяем угол нагрузки
;
3) под углом наносим линию направления , величина пока не известна;
4)
определяем
(угол
)
по фактическому значению
согласно (3.15);
5)
под углом
наносим вектор
(отрезок Om);
6)
аналогично находим
(угол
);
7)
под углом
наносим направление вектора
.
Вектор
еще не определен, поэтому можно найти
только его направление;
8)
от конца вектора
(точка m)
наносим прямую, параллельную
;
9)
так как
известно по величине, от точки O циркулем
делаем засечку радиусом, равным величине
.
Получаем треугольник Omn.
Вектор
состоит из суммы двух векторов —
и
.
Тогда
(отрезок On)
будет третьей стороной треугольника
Omn;
10)
абсолютное значение
можно определить делением абсолютных
значений:
/
.
Такая
диаграмма строится как для максимального
( см. приложение, рис. 1), так и для
минимального (см. приложение, рис. 2)
режимов. При этом для максимального
режима используются
(
)
и
,
а для минимального режима —
(
)
и
(в режиме
).
Зная
абсолютные значения напряжений в начале
и в конце
линии, можно определить потерю напряжения
для любого режима. Наибольшую потерю
напряжения в большинстве случаев дает
максимальный режим, т. е.:
. (4.4)
Максимальный режим:
А;
º;
º;
;
;
º;
кВ.
Минимальный режим:
А;
º;
º;
;
;
º;
кВ.
Потери напряжения:
кВ;
;
кВ.
5. Определение коэффициентов трансформации
Требуемые коэффициенты трансформации по условиям стабильности напряжения у потребителя с учетом заданных отклонений будут различными в разных режимах:
,
(5.1)
Если
согласно рассматриваемому примеру
напряжение на шинах С в конце передачи
,
то в максимальном и минимальном режимах
соответственно:
; (5.2)
.
Регулирование напряжения заключается в следующем: при изменении режимов коэффициенты трансформации меняются так, чтобы обеспечить диапазон отклонений напряжения на шинах С согласно заданию (±2 %).
Для фазных величин это выразится неравенством:
; (5.3)
;
кВ;
;
кВ;
;
.
;
.
Выбор
ответвлений у трансформаторов производится
так, чтобы обеспечить напряжение у
потребителей согласно выражению (5.3).
Следовательно, ответвление на подстанции
В (ответвления, как правило, делаются
на стороне высшего напряжения
трансформаторов) в максимальном режиме
должно быть равно или меньше напряжения
,
а в минимальном — равно или больше
напряжения
.
;
;
;
.
При изменении режима регулятор переключает ответвления в пределах от 313,5 до 333,3 кВ. Следует проверить наличие приемлемых ответвлений у выбранного трансформатора.
Отклонения требуемых ответвлений от номинального напряжения 330 кВ составляют в максимальном и минимальном режимах соответственно:
%;
%.
Поскольку данный трансформатор имеет пределы регулирования 8 %, он обеспечивает требуемое напряжение на шинах С в максимальном режиме.
ЗАКЛЮЧЕНИЕ
При расчете курсового проекта расчет линии длиной = 100 км;
электропередачи
выбираем марку провода АС-120 активные
и индуктивные сопротивления линии
Ом,
Ом,
активные и реактивная проводимость
См.
См
Трансформатор
ТРДН 40000/110
активные и
индуктивные сопротивления трансформатора
Ом
Ом, активные
и реактивные проводимости трансформаторов
См,
См,
коэффициенты трансформации
,
.
Отклонения требуемых ответвлений от
номинального напряжения 110 кВ не превышают
номинальных значений трансформатора,
составляют в максимальном и минимальном
режимах соответственно: 5% и 0,75 % Поскольку
данный трансформатор имеет пределы
регулирования
8 %, он обеспечивает требуемое напряжение
на шинах в максимальном режиме.
ЛИТЕРАТУРА
1.Пособие по к курсовому и дипломному проектированию для электроэнергетических специальностей ВУЗов / Под. ред. В.М. Блок.- М.: Высш. шк., 1990.- 383 с.
2. Проектирование электротехнических устройств: Методические указания по выполнению курсовой работы для студентов спец. 181300 электроэнергетического факультета. – Вологда: ВоГТУ, 2000
ПРИЛОЖЕНИЕ
Графическое определение напряжения в конце передачи для максимального и минимального режима
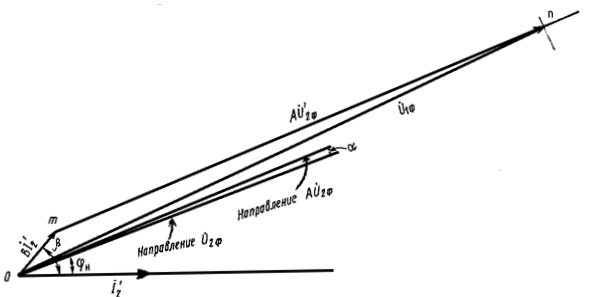
Рис. 1.