3.3 Гипергеометрическое рапределение

Имеется N объектов. Из них n объектов обладают требуемым свойством. Из общего количества отбирается m объектов. Случайная величина X - число объектов из m отобранных, обладающих требуемым свойством. Для вычисления вероятностей используются биномиальные коэффициенты (см. число сочетаний). Закон распределения имеет вид:

Пример 3.3

Срди 20 книг, стоящих на полке, 8 книг по математической статистике. Случайная величина X - число книг по математике из четырёх случайно взятых с этой полки книг. Составить ряд распределения, найти функцию распределения, построить её график и найти все числовые характеристики.

Решение Случайная величина X может принимать значения 0, 1, 2, 3, 4. P(0)=C⁴₁₂/C⁴₂₀=(12!16!4!)/(4!8!20!)=(9·10·11·12)/(17·18·19·20)≈0,102167 P(1)=(C³₁₂·C¹₈)/C⁴₂₀=(12!·8·16!4!)/(3!9!20!)=(10·11·12·8·4)/(17·18·19·20)≈0,363261 P(2)=(C²₁₂·C²₈)/C⁴₂₀≈0,381424 P(3)=(C¹₁₂·C³₈)/C⁴₂₀≈0,138700 P(4)=C⁴₈/C⁴₂₀≈0,014448 Ряд распределения: x_i|    0    |    1    |     2     |     3     |     4 ------------------------------------------------ p_i|0,1022|0,3633|0,38143|0,13873|0,0145

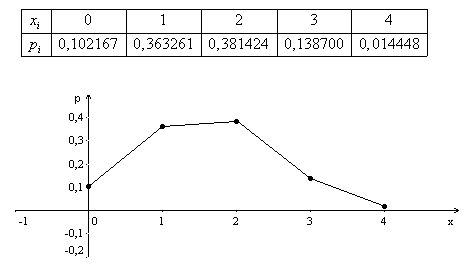
Функция распределения - это вероятность того, что случайная величина примет значение меньшее, чем конкретное числовое значение x. Её значения находим суммированием вероятностей. При       x ≤ 0   F(X) = 0 При 0 ≤ x ≤ 1   F(X) = 0,102167 При 1 ≤ x ≤ 2   F(X) = 0,102167 + 0,363261 = 0,465428 При 2 ≤ x ≤ 3   F(X) = 0,465428 + 0,381424 = 0,846852 При 3 ≤ x ≤ 4   F(X) = 0,846852 + 0,138700 = 0,985552 При       x ≥ 4   F(X) = 0,985552 + 0,014448 = 1

M(X) = 0·0,1022 + 1·0,3633 + 2·0,38143 + 3·0,13873 + 4·0,0145 = 1,6 D(X) = 0²·0,1022 + 1²·0,3633 + 2²·0,38143 + 3²·0,13873 + 4²·0,0145 - 1,6² ≈ 0,808421 σ(Х) ≈ 0,899 Свернуть

3.4 Распределение Пуассона

Пусть имеется некоторая последовательность событий, наступающих в случайные моменты времени (будем называть это потоком событий). Интенсивность потока (среднее число событий, появляющихся в единицу времени) равна λ. Пусть этот поток событий - простейший (пуассоновский), т.е. обладает тремя свойствами: 1) вероятность появления k событий за определённый промежуток времени зависит только от длины этого промежутка, но не от точки отсчёта, другими словами, интенсивность потока есть постоянная величина (свойствостационарности); 2) вероятность появления k событий в любом промежутке времени не зависит от того, появлялись события в прошлом или нет (свойство «отсутствия последействия»); 3) появление более одного события за малый промежуток времени практически невозможно (свойствоординарности). Вероятность того, что за промежуток времени t событие произойдёт k раз, равна

Пример 3.4

Среднее число вызовов, поступающих на АТС за 1 мин, равно двум. Найти вероятность того, что за 4 мин. поступит: а) три вызова; б)менее трёх вызовов; в)не менее трёх вызовов. Поток вызовов - простейший.

Решение Используем формулу Пуассона. λ = 2, t = 4. P(0) = 8⁰/0!·e^-8 = e^-8 ≈ 0,000335 P(1) = 8¹/1!·e^-8 = 8e^-8 ≈ 0,002684 P(2) = 8²/2!·e^-8 = 32e^-8 ≈ 0,010735 P(3) = 8³/3!·e^-8 = 85,33e^-8 ≈ 0,014313 а) P(k=3) = 0,014313 б) P(k<3) = P(0) + P(1) + P(2) = 0,013754 в) P(k≥3) = 1 - P(k<3) = 1 - 0,013754 = 0,986246 Свернуть