
- •I програма курсу
- •II загальні методичні вказівки
- •Правила оформлення контрольної роботи
- •III основні поняття курсу
- •3.1. Елементи комбінаторики
- •3.2. Види подій
- •3.3. Різні визначення ймовірності
- •Класичне визначення ймовірності
- •Статистичне визначення ймовірності
- •Геометричне визначення ймовірності
- •3.4. Основні теореми і формули
- •Д) Виходячи з того, що сума подій полягає в появі хоча б одного з подій – складових, має сенс користатися іншою формулою:
- •Формула повної ймовірності
- •Формула Бейєса
- •IV. Повторні випробування
- •Формула Пуассона
- •Локальна теорема Лапласа
- •V. Випадкові величини та їх характеристики
- •5.1. Поняття про випадкові величини
- •5.2. Функції розподілу
- •Властивості інтегральної функції
- •Властивості диференціальної функції
- •5.3. Числові характеристики випадкових величин
- •5.4. Конкретні закони розподілу
- •5.5. Закон великих чисел
- •VI. Елементи математичної статистики
- •6.1. Характеристики розподілу вибіркових даних
- •6.2. Побудова законів розподілу за вибірковими даними
- •Побудова нормального закону за емпіричним варіаційним рядом Припустимо, що у результаті випробування отримано інтервальний варіаційний ряд ознаки
- •Обчислення теоретичного ряду частот нормального розподілу
- •Побудова закону Пуассона по емпіричному матеріалу
- •Нехай отримано емпіричний варіаційний ряд ознаки
- •Обчислення теоретичного ряду частот розподілу Пуассона
- •6.3. Критерії згоди. Основні поняття
- •Критерій згоди Пірсона
- •Критерій згоди Колмогорова
- •Критерій згоди Ястремського
- •Критерій згоди Романовського
- •6.4. Лінійна кореляція і рівняння лінійної регресії
- •IV застосування комп’ютерних засобів для рішення деяких задач статистики
- •Введення даних
- •Графічне представлення даних
- •Статистичний аналіз даних в Excel
- •VIII. Завдання для контрольної роботи
- •I. Розв’язати задачі
- •Іi. Розв’язати задачі
- •IV. Розв’язати задачі
- •V. Для дискретної випадкової величини х, заданої рядом розподілу, знайти:
- •VI. Неперервна випадкова величина х задана інтегральною функцією
- •IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
- •Додаток 1
- •Додаток 2
- •Продовження додатку 2
- •Критичні точки розподілу
- •Значення (розподіл Пуассона)
- •Критерій Колмогорова
- •Критерій Колмогорова
V. Випадкові величини та їх характеристики
5.1. Поняття про випадкові величини
Випадковою величиною називають таку змінну, яка в результаті випробування може приймати одне з можливих значень, причому заздалегідь невідомо, яке саме.
Наприклад, число улучень при п’ятьох пострілах, зріст людини.
Дискретною (перервною) називається випадкова величина, яка може приймати окремі, ізольовані значення з деякого інтервалу.
Наприклад, число улучень в мішень при 10 пострілах.
Неперервною називається випадкова величина, яка може приймати кожне значення з деякого інтервалу.
Наприклад, зріст людини, помилка при вимірюванні деталей.
Законом розподілу випадкової величини називається всяке співвідношення, що встановлює зв’язок між можливими значеннями випадкової величини та їх ймовірностями.
Закон розподілу можна задати табличним, графічним та аналітичним способами.
Ряд розподілу – це перелік усіх можливих значень дискретної випадкової величини і відповідних їм ймовірностей.
|
|
|
… |
|
|
|
|
… |
|
Сума ймовірностей усіх можливих значень дискретної випадкової величини дорівнює одиниці
![]() .
.
З метою наочності ряд розподілу
дискретної випадкової величини можна
зобразити графічно, для чого в прямокутній
системі координат будують точки
![]() і з’єднують їх відрізками прямих.
Отриману фігуру називають багатокутником
або полігоном розподілу
.
і з’єднують їх відрізками прямих.
Отриману фігуру називають багатокутником
або полігоном розподілу
.
5.2. Функції розподілу
Дискретні і неперервні випадкові величини можна задавати за допомогою інтегральної функції розподілу.
Інтегральною
функцією розподілу (або
функцією
розподілу) називається
функція
![]() ,
що визначає для кожного значення
,
що визначає для кожного значення
![]() ймовірність того, що випадкова величина
прийме значення, менше числа
ймовірність того, що випадкова величина
прийме значення, менше числа
![]() .
.
Властивості інтегральної функції
Значення інтегральної функції належать відрізку
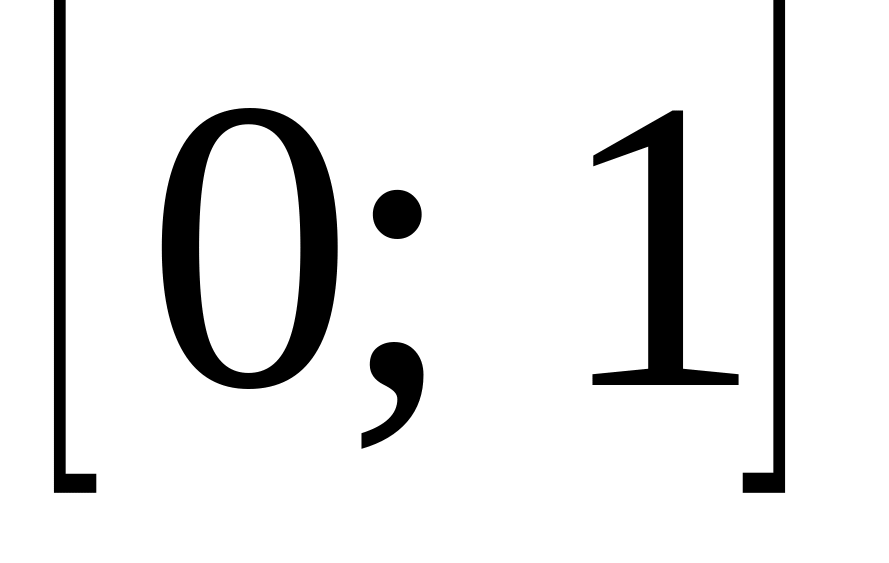 .
.Інтегральна функція є неспадною функцією свого аргументу.
Ймовірність того, що випадкова величина прийме яке-небудь значення з інтервалу
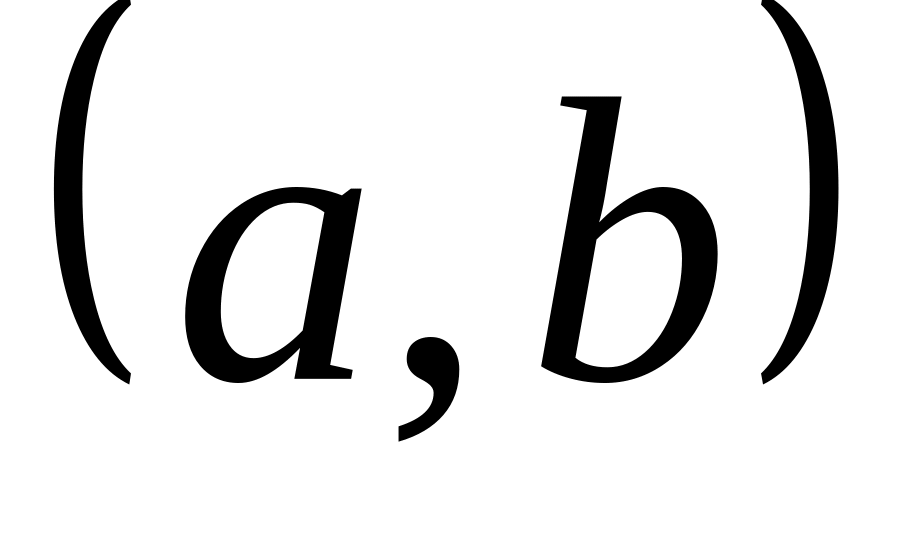 ,
дорівнює приросту інтегральної функції
на цьому інтервалі
,
дорівнює приросту інтегральної функції
на цьому інтервалі
![]() .
.
Неперервні випадкові величини можна задавати за допомогою диференціальної функції.
Диференціальною
функцією розподілу або густиною
ймовірності
називається перша похідна від інтегральної
функції
![]()
Кривою розподілу неперервної випадкової величини називають графік її густини ймовірності.
Властивості диференціальної функції
Диференціальна функція є невід’ємною
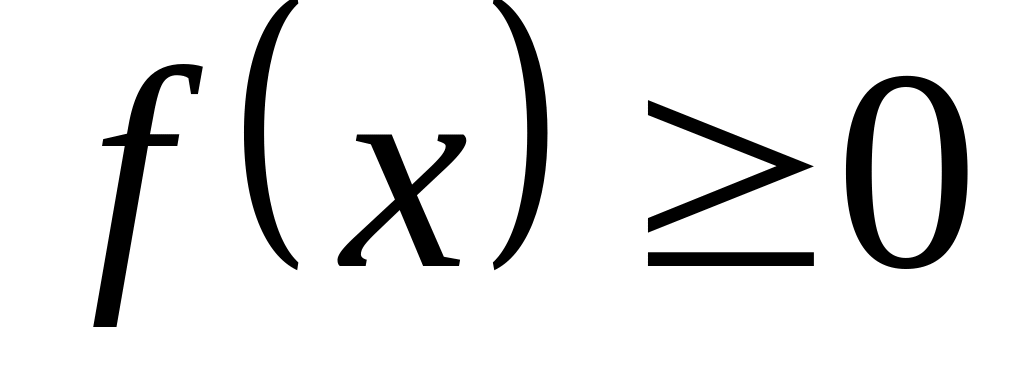 .
.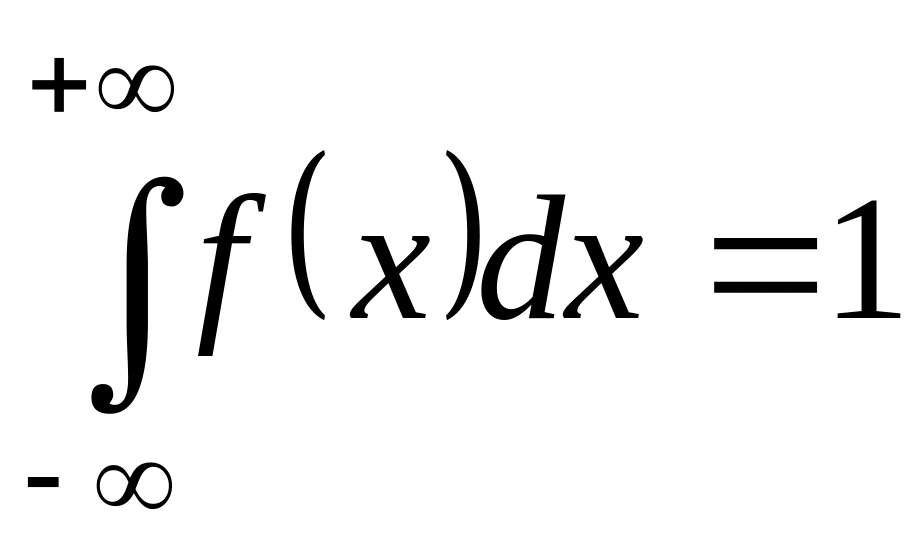 .
.Ймовірність того, що неперервна випадкова величина прийме будь-яке значення з інтервалу дорівнює визначеному інтегралу від густини розподілу на цьому інтервалі
![]() .
.
Зв’язок між інтегральною і диференціальною функціями
![]() ,
,
![]() .
.
5.3. Числові характеристики випадкових величин
Числовими характеристиками випадкової величини називаються характеристики, які у стислій формі виражають найбільш суттєві особливості розподілу.
Математичне сподівання (середнє значення).
Для дискретної випадкової величини –
![]() .
.
Для неперервної випадкової величини –
![]() .
.
Властивості математичного сподівання
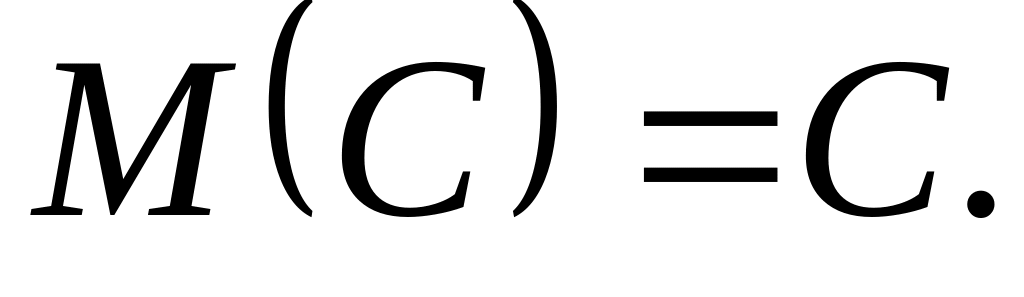
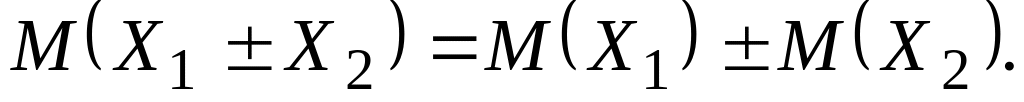
 – для незалежних випадкових
величин.
– для незалежних випадкових
величин.
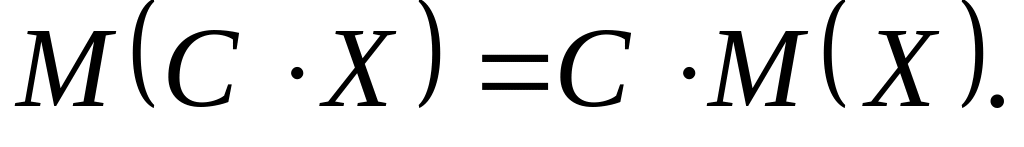
Дисперсія (міра розсіювання) –
![]() ,
,
 – для дискретної випадкової
величини,
– для дискретної випадкової
величини,
![]() – для неперервної випадкової
величини.
– для неперервної випадкової
величини.
Властивості дисперсії

 .
.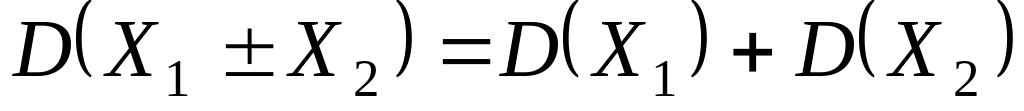 – для незалежних випадкових
величин.
– для незалежних випадкових
величин. .
.
Середнє квадратичне відхилення –
![]() .
.
