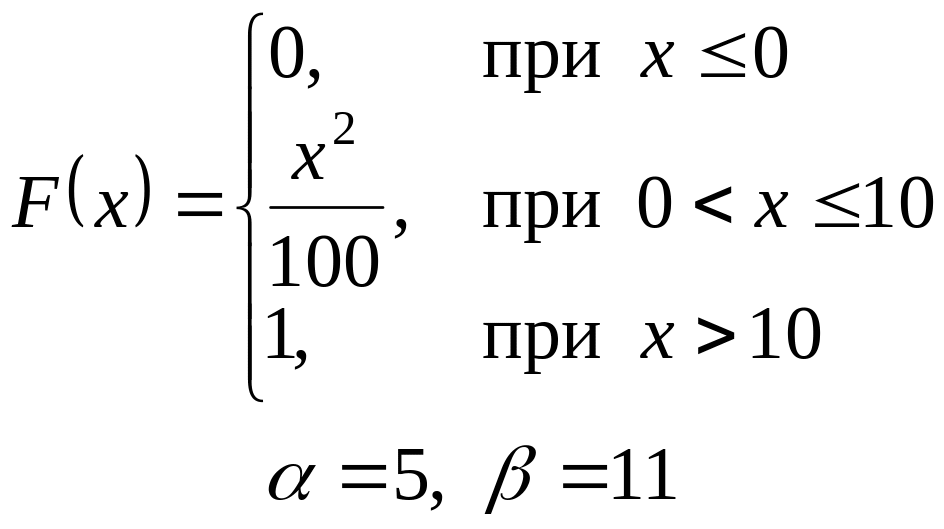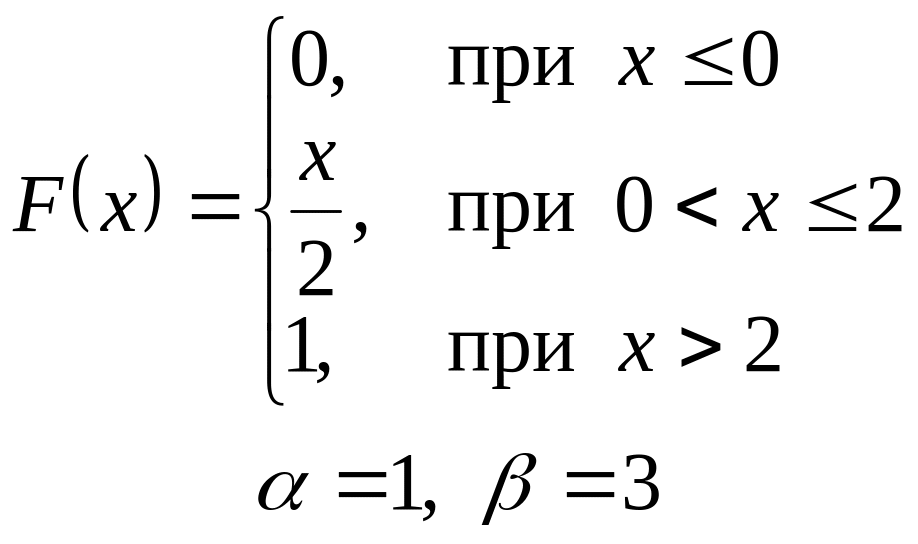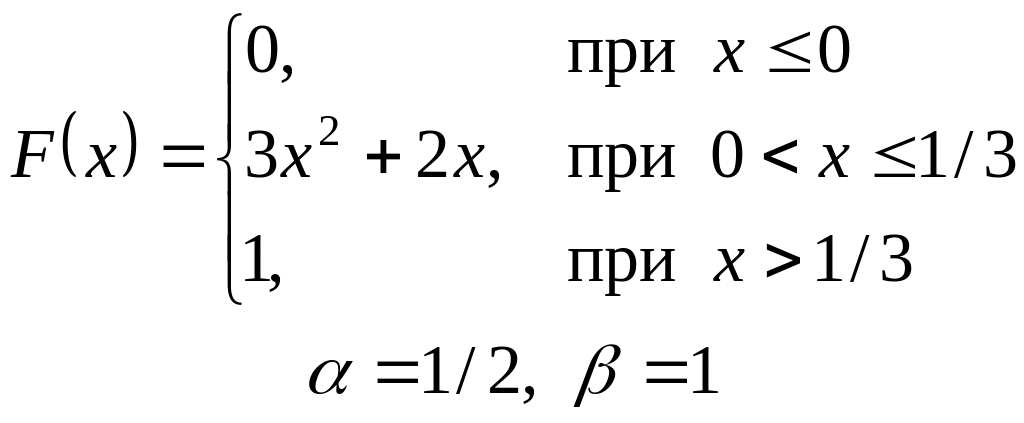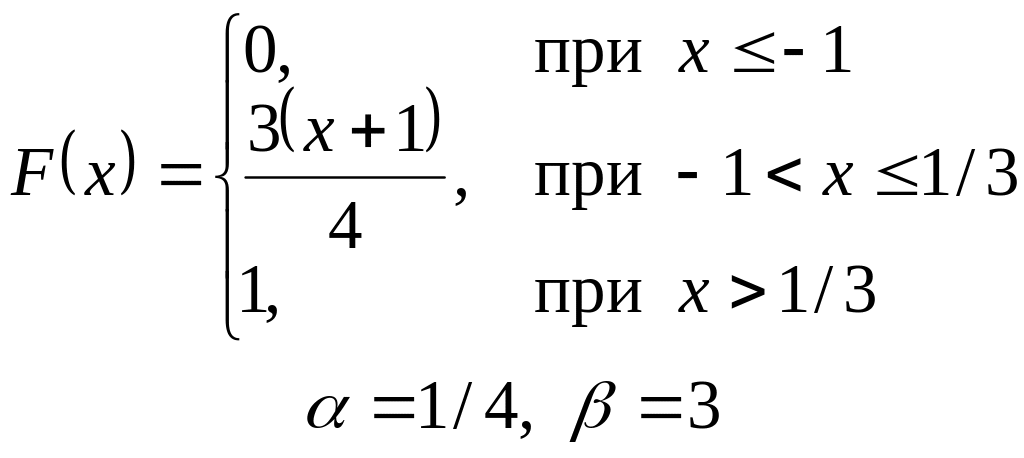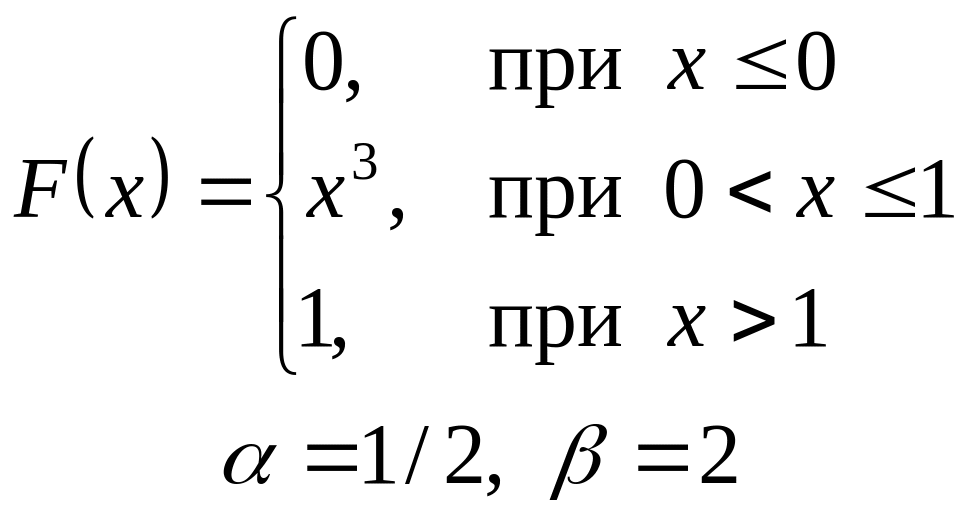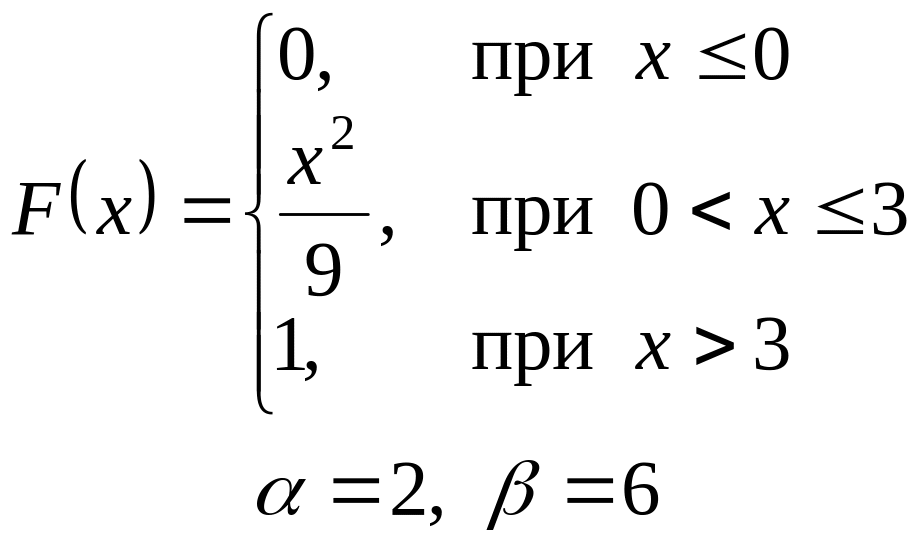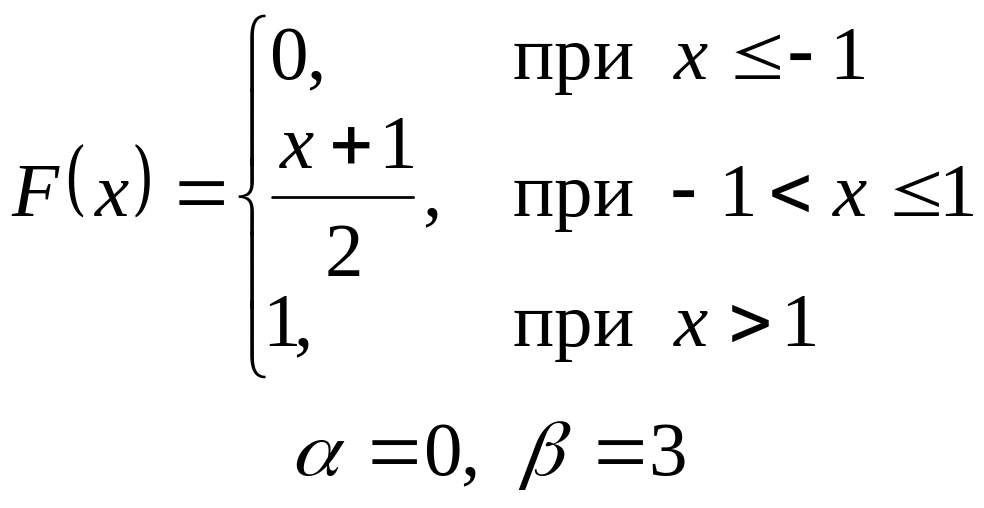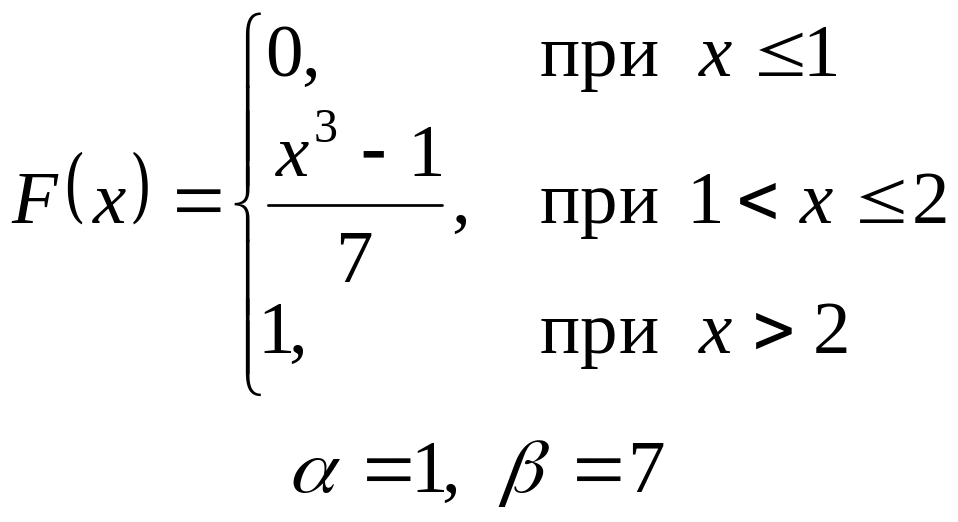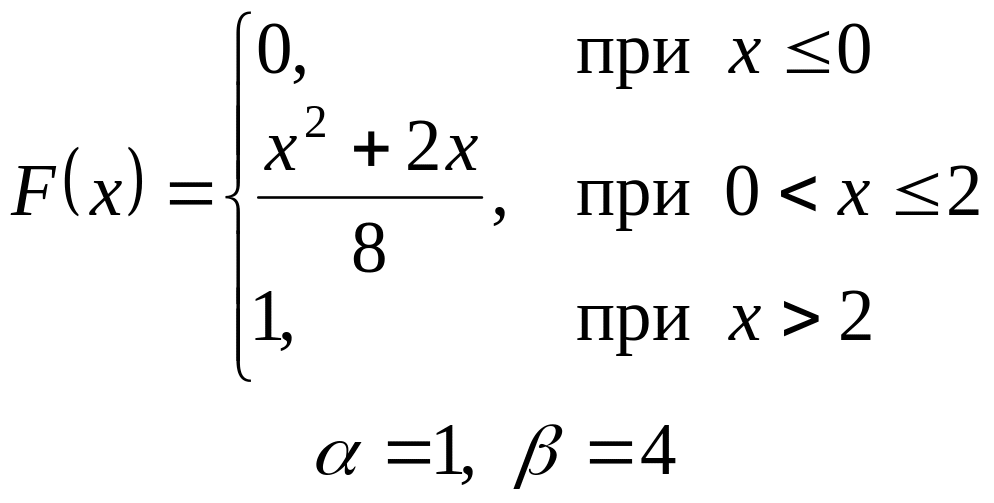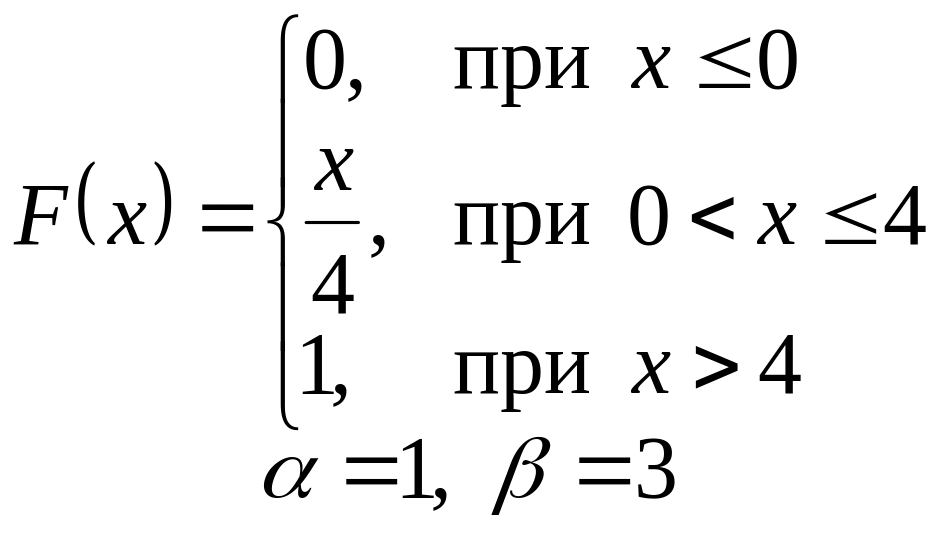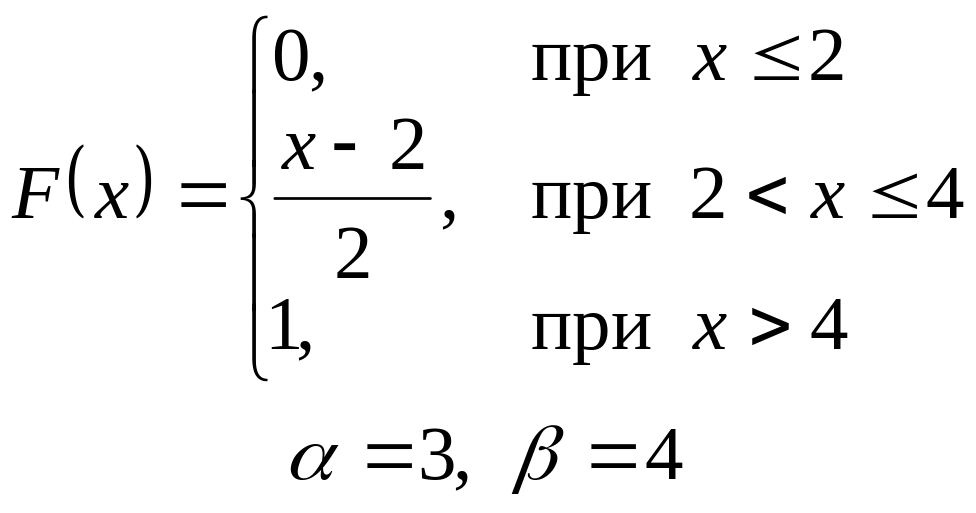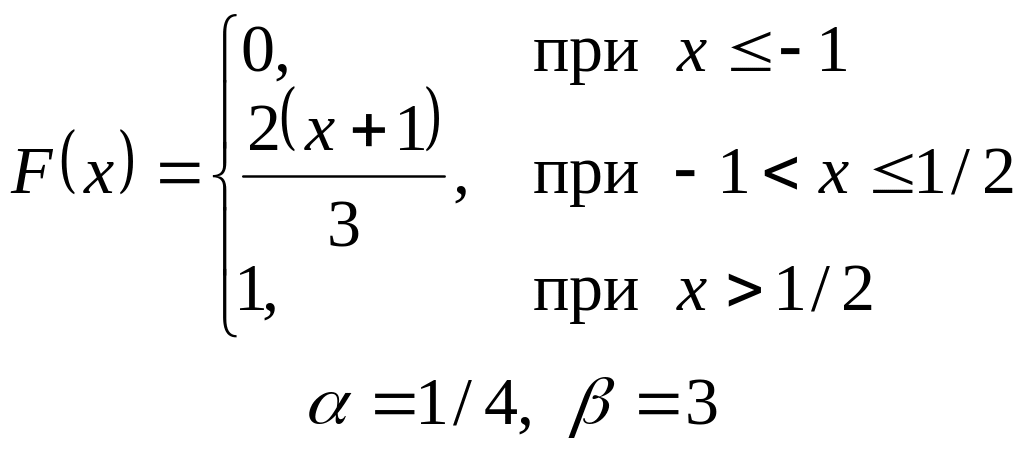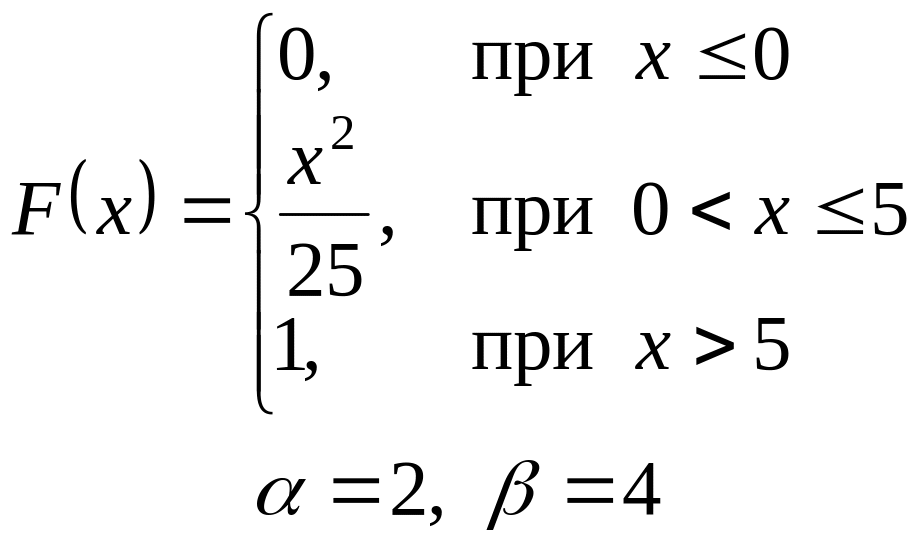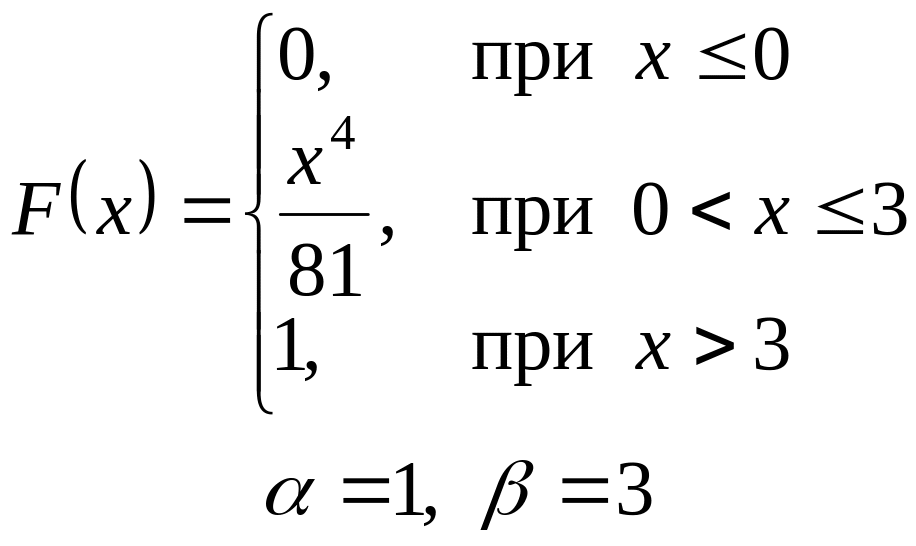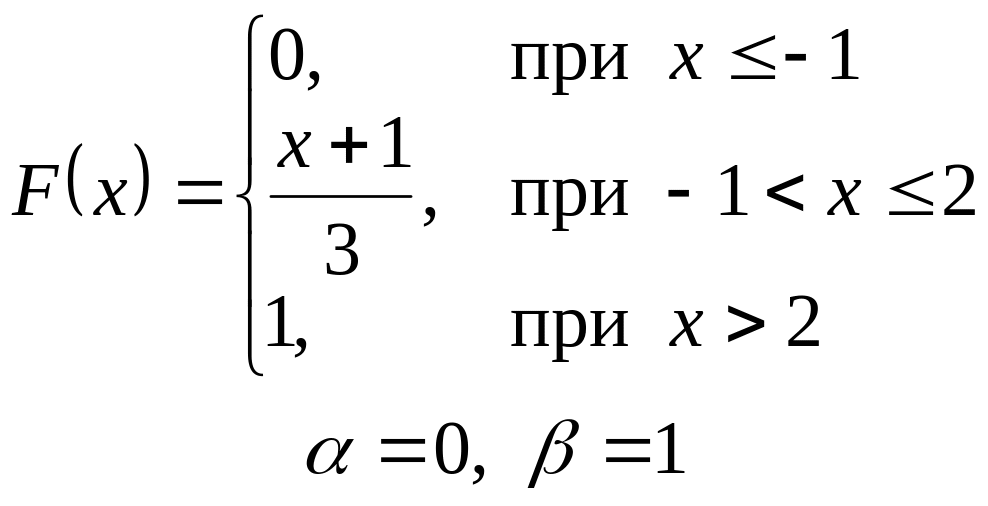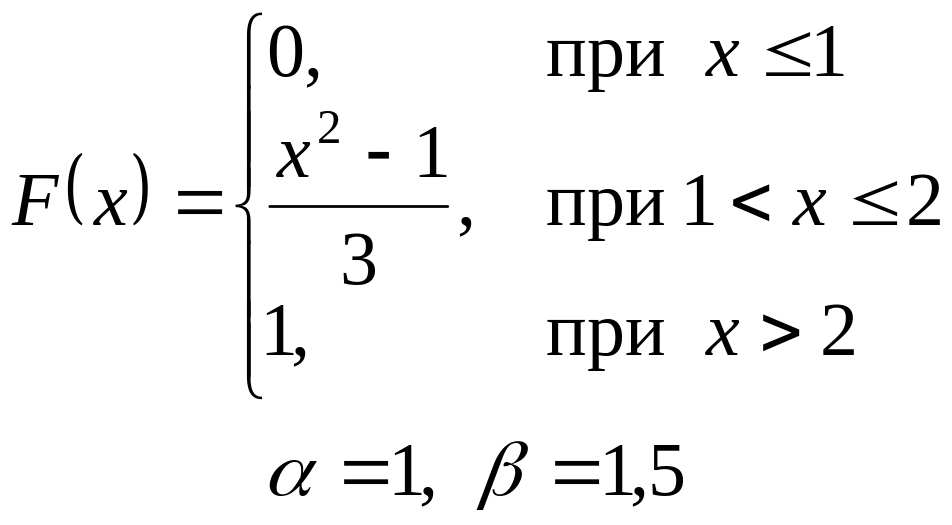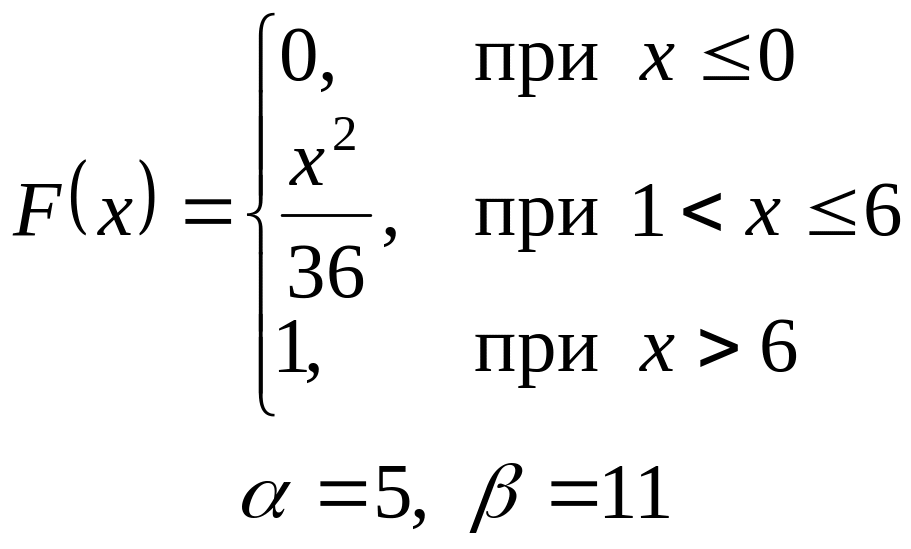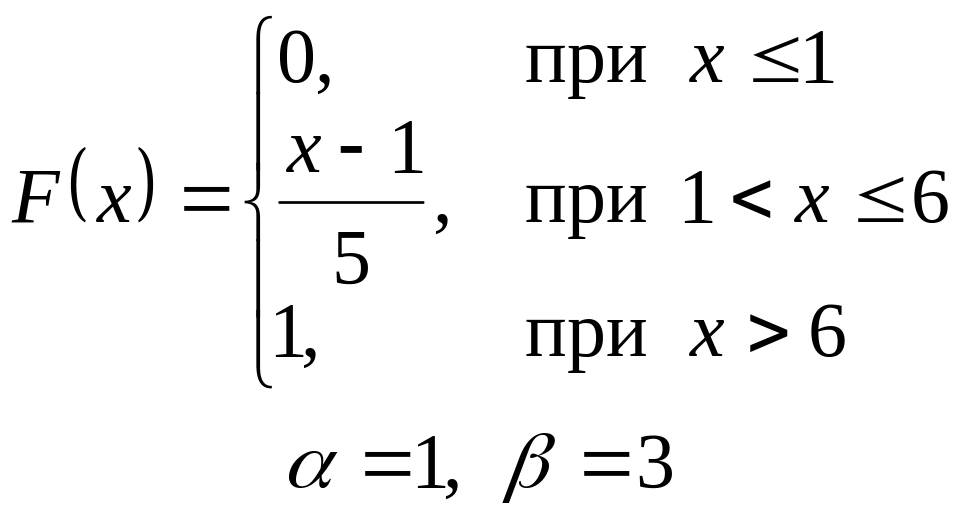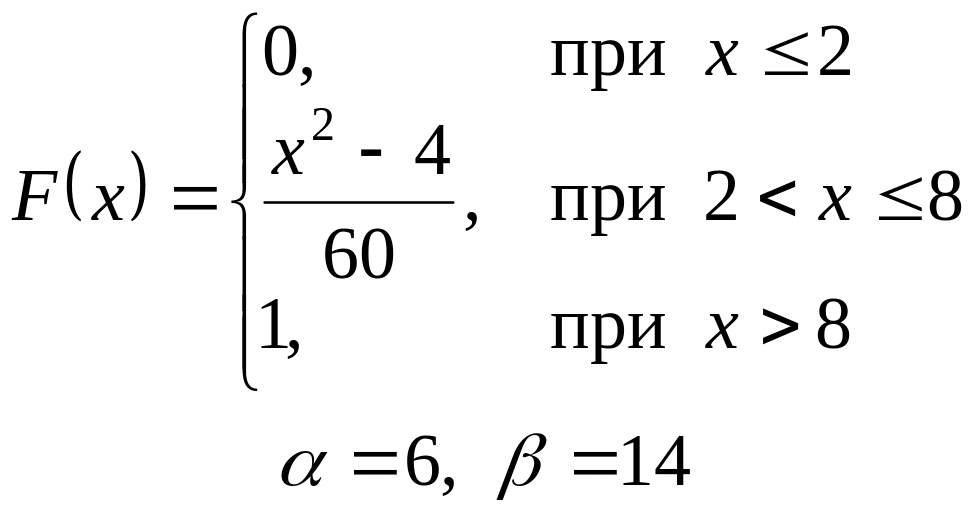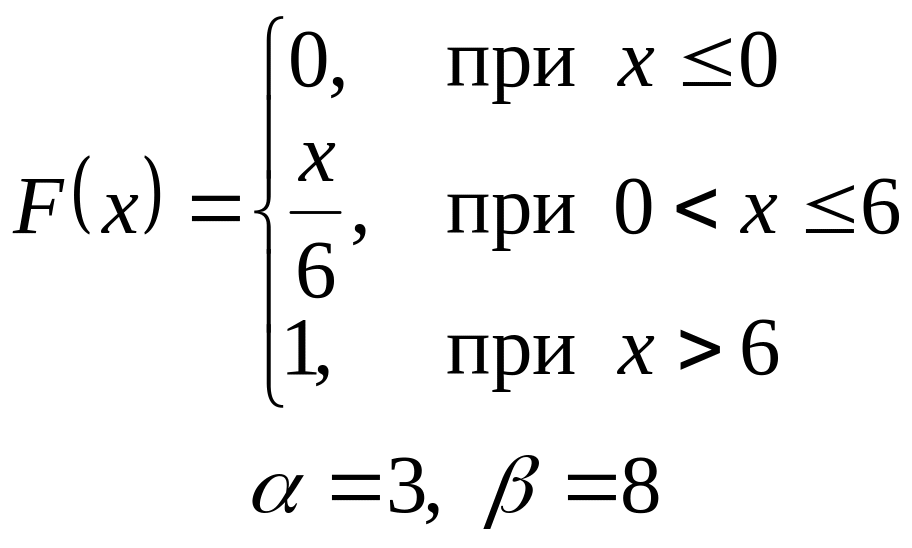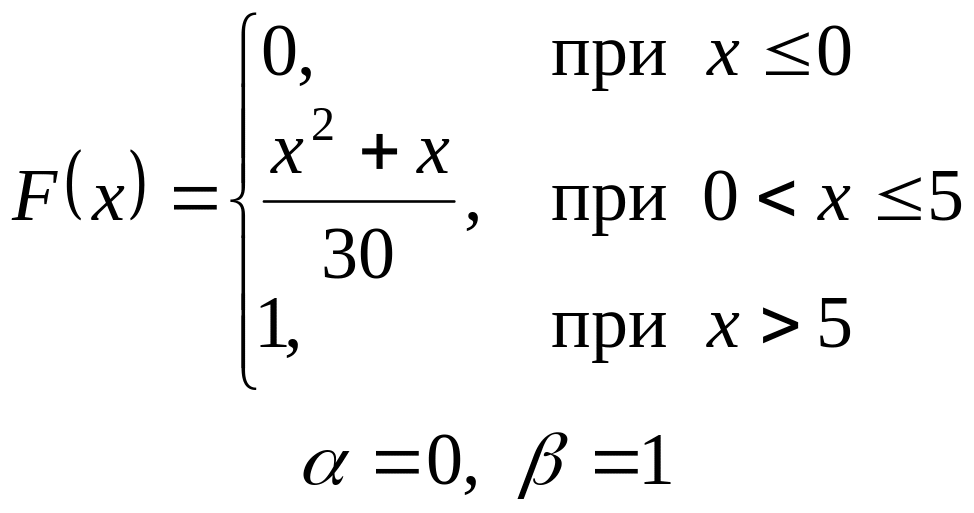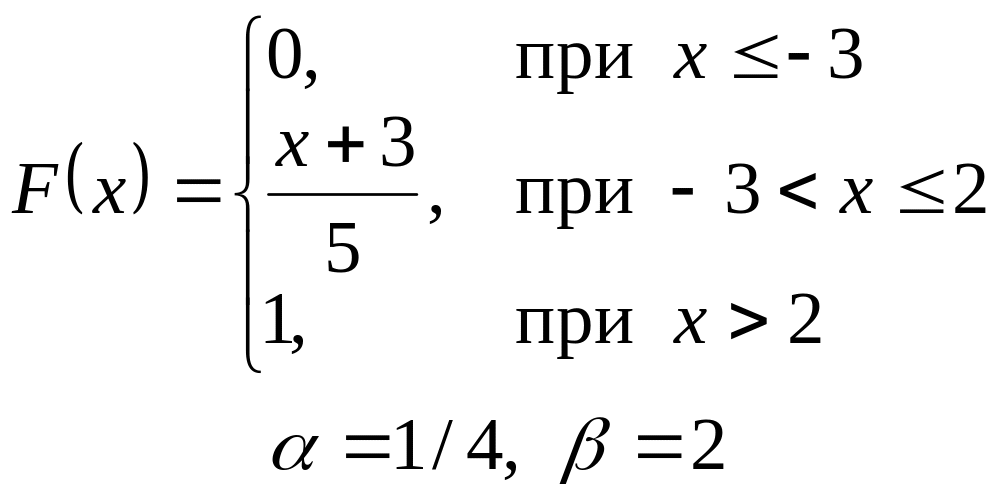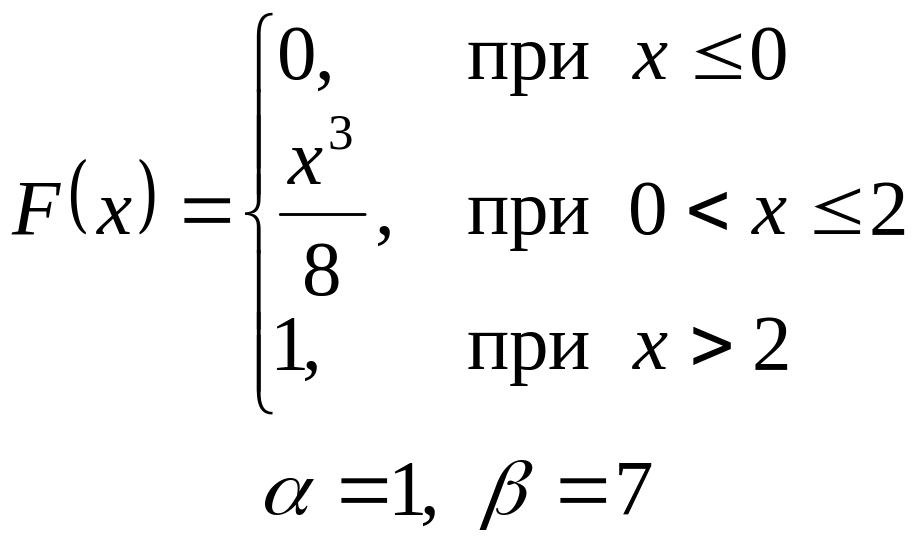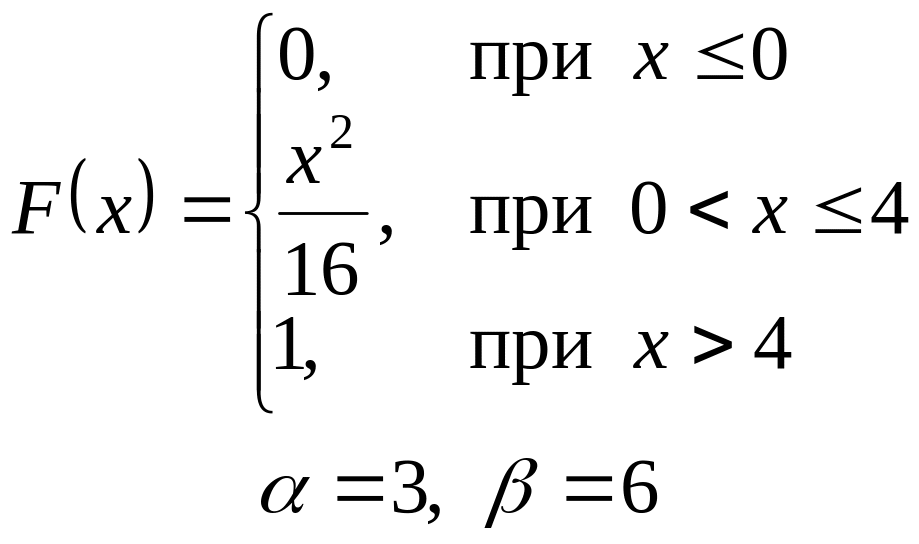VI. Неперервна випадкова величина х задана інтегральною функцією
розподілу. Знайти:
а) диференціальну функцію (густину розподілу ймовірності);
б) ймовірність попадання
випадкової величини в інтервал
;
в) математичне сподівання і дисперсію;
г) побудувати графіки , .
1. |
|
2. |
|
|
|
||
3. |
|
4. |
|
|
|||
|
|
|
|||||
5. |
|
6. |
|
|
|||
|
|
|
|||||
7. |
|
8. |
|
|
|||
|
|
|
|||||
9. |
|
10. |
|
||||
|
|
||||||
11. |
|
12. |
|
||||
|
|
||||||
13. |
|
14. |
|
||||
|
|
||||||
15. |
|
16. |
|
|
|
||
17. |
|
18. |
|
|
|
||
19. |
|
20. |
|
|
|
||
21. |
|
22. |
|
|
|
||
23. |
|
24. |
|
|
|
||
25. |
|
26. |
|
|
|
||
27. |
|
28. |
|
|
|
||
29. |
|
30. |
|
|
|
||
VII. За спостереженнями над ознакою Х складений статистичний розподіл вибірки. Побудувати полігон відносних частот і кумулятивну криву. Знайти емпіричну функцію і побудувати її графік. Обчислити вибіркову середню, дисперсію і середнє квадратичне відхилення.
1. |
|
12 |
15 |
17 |
20 |
24 |
|
2. |
|
13 |
16 |
18 |
21 |
25 |
|
4 |
5 |
10 |
8 |
3 |
|
|
5 |
6 |
11 |
9 |
4 |
3. |
|
11 |
14 |
16 |
19 |
23 |
|
4. |
|
9 |
10 |
21 |
28 |
29 |
|
3 |
4 |
9 |
7 |
2 |
|
|
2 |
4 |
8 |
3 |
11 |
5. |
|
10 |
13 |
16 |
20 |
24 |
|
6. |
|
10 |
13 |
15 |
18 |
23 |
|
3 |
2 |
5 |
7 |
6 |
|
|
2 |
3 |
8 |
6 |
1 |
7. |
|
6 |
9 |
11 |
13 |
18 |
|
8. |
|
12 |
16 |
18 |
19 |
22 |
|
2 |
6 |
3 |
10 |
7 |
|
|
6 |
2 |
4 |
5 |
8 |
9. |
|
5 |
6 |
8 |
9 |
12 |
|
10. |
|
13 |
15 |
19 |
22 |
25 |
|
2 |
8 |
3 |
4 |
6 |
|
|
2 |
8 |
3 |
1 |
9 |
11. |
|
13 |
16 |
18 |
22 |
27 |
|
12. |
|
14 |
15 |
19 |
21 |
23 |
|
5 |
4 |
3 |
9 |
11 |
|
|
3 |
4 |
9 |
13 |
12 |
13. |
|
11 |
14 |
19 |
23 |
26 |
|
14. |
|
16 |
18 |
19 |
22 |
27 |
|
2 |
4 |
9 |
3 |
12 |
|
|
7 |
3 |
16 |
2 |
14 |
15. |
|
10 |
15 |
19 |
22 |
28 |
|
16. |
|
11 |
15 |
16 |
19 |
24 |
|
6 |
2 |
7 |
2 |
10 |
|
|
5 |
1 |
13 |
14 |
8 |
17. |
|
3 |
9 |
12 |
20 |
26 |
|
18. |
|
9 |
11 |
13 |
19 |
20 |
|
5 |
1 |
9 |
18 |
15 |
|
|
5 |
11 |
9 |
6 |
8 |
19. |
|
12 |
15 |
19 |
23 |
29 |
|
20. |
|
6 |
12 |
15 |
18 |
22 |
|
8 |
3 |
1 |
5 |
2 |
|
|
5 |
12 |
4 |
8 |
1 |
21. |
|
6 |
8 |
15 |
19 |
21 |
|
22. |
|
13 |
18 |
19 |
22 |
26 |
|
2 |
8 |
3 |
15 |
1 |
|
|
7 |
2 |
13 |
4 |
3 |
23. |
|
16 |
18 |
20 |
25 |
27 |
|
24. |
|
10 |
11 |
16 |
19 |
21 |
|
5 |
2 |
4 |
17 |
3 |
|
|
2 |
1 |
5 |
16 |
14 |
25. |
|
10 |
15 |
25 |
27 |
29 |
|
26. |
|
14 |
16 |
17 |
19 |
25 |
|
13 |
15 |
17 |
6 |
4 |
|
|
3 |
4 |
9 |
12 |
8 |
27. |
|
9 |
12 |
16 |
21 |
26 |
|
28. |
|
17 |
19 |
21 |
23 |
27 |
|
9 |
2 |
14 |
13 |
5 |
|
|
1 |
9 |
7 |
14 |
19 |
29. |
|
12 |
16 |
19 |
22 |
27 |
|
30. |
|
16 |
20 |
21 |
23 |
26 |
|
6 |
21 |
13 |
5 |
17 |
|
|
2 |
8 |
14 |
13 |
5 |
VIII. У припущенні про нормальний розподіл ознаки знайти теоретичні частоти за допомогою інтегральної функції розподілу і густини ймовірності. Перевірити на основі критеріїв Пірсона, Колмогорова, Романовського погодженість фактичних і теоретичних частот
1.
|
1-2 |
2-3 |
3-4 |
4-5 |
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
|
2 |
8 |
26 |
65 |
120 |
181 |
201 |
170 |
120 |
64 |
28 |
10 |
3 |
2.
|
2-3 |
3-4 |
4-5 |
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
14-15 |
|
1 |
6 |
19 |
47 |
86 |
130 |
145 |
122 |
86 |
46 |
20 |
7 |
2 |
3.
|
3-4 |
4-5 |
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
14-15 |
15-16 |
|
1 |
4 |
14 |
34 |
62 |
94 |
105 |
88 |
62 |
33 |
15 |
5 |
2 |
4.
|
4-5 |
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
14-15 |
15-16 |
16-17 |
|
2 |
6 |
20 |
49 |
90 |
136 |
151 |
128 |
90 |
48 |
21 |
8 |
2 |
5.
|
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
14-15 |
15-16 |
16-17 |
17-18 |
|
2 |
7 |
21 |
53 |
98 |
148 |
165 |
139 |
98 |
52 |
23 |
8 |
2 |
6.
|
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
14-15 |
15-16 |
16-17 |
17-18 |
18-19 |
|
1 |
6 |
19 |
48 |
89 |
135 |
150 |
127 |
89 |
48 |
21 |
7 |
2 |
7.
|
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
14-15 |
15-16 |
16-17 |
17-18 |
18-19 |
19-20 |
|
2 |
6 |
20 |
50 |
92 |
139 |
155 |
131 |
92 |
49 |
22 |
8 |
2 |
8.
|
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
14-15 |
15-16 |
16-17 |
17-18 |
18-19 |
19-20 |
20-21 |
|
2 |
7 |
22 |
55 |
101 |
152 |
169 |
143 |
101 |
54 |
24 |
8 |
3 |
9.
|
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
14-15 |
15-16 |
16-17 |
17-18 |
18-19 |
19-20 |
20-21 |
21-22 |
|
2 |
6 |
21 |
53 |
97 |
147 |
163 |
138 |
97 |
52 |
23 |
8 |
2 |
10.
|
10-11 |
11-12 |
12-13 |
13-14 |
14-15 |
15-16 |
16-17 |
17-18 |
18-19 |
19-20 |
20-21 |
21-22 |
22-23 |
|
2 |
7 |
23 |
58 |
107 |
161 |
179 |
151 |
107 |
57 |
25 |
9 |
3 |
11.
|
1-2 |
2-3 |
3-4 |
4-5 |
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
|
1 |
6 |
18 |
45 |
83 |
126 |
140 |
118 |
83 |
44 |
19 |
7 |
2 |
12.
|
2-3 |
3-4 |
4-5 |
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
14-15 |
|
2 |
7 |
24 |
59 |
109 |
164 |
182 |
154 |
109 |
58 |
25 |
9 |
3 |
13.
|
3-4 |
4-5 |
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
14-15 |
15-16 |
|
2 |
7 |
22 |
56 |
103 |
156 |
173 |
146 |
103 |
55 |
24 |
9 |
3 |
14.
|
4-5 |
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
14-15 |
15-16 |
16-17 |
|
1 |
4 |
13 |
33 |
61 |
91 |
102 |
86 |
61 |
32 |
14 |
5 |
2 |
15.
|
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
14-15 |
15-16 |
16-17 |
17-18 |
|
1 |
4 |
14 |
36 |
66 |
99 |
110 |
93 |
66 |
35 |
15 |
5 |
2 |
16.
|
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
14-15 |
15-16 |
16-17 |
17-18 |
18-19 |
|
1 |
5 |
15 |
38 |
70 |
105 |
117 |
99 |
70 |
37 |
16 |
6 |
2 |
17.
|
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
14-15 |
15-16 |
16-17 |
17-18 |
18-19 |
19-20 |
|
2 |
7 |
24 |
60 |
112 |
168 |
187 |
158 |
112 |
60 |
26 |
9 |
3 |
18.
|
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
14-15 |
15-16 |
16-17 |
17-18 |
18-19 |
19-20 |
20-21 |
|
2 |
7 |
21 |
53 |
98 |
148 |
164 |
139 |
98 |
52 |
23 |
8 |
2 |
19.
|
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
14-15 |
15-16 |
16-17 |
17-18 |
18-19 |
19-20 |
20-21 |
21-22 |
|
2 |
7 |
23 |
58 |
107 |
162 |
180 |
152 |
107 |
57 |
25 |
9 |
3 |
20.
|
10-11 |
11-12 |
12-13 |
13-14 |
14-15 |
15-16 |
16-17 |
17-18 |
18-19 |
19-20 |
20-21 |
21-22 |
22-23 |
|
2 |
7 |
23 |
57 |
106 |
159 |
177 |
150 |
106 |
56 |
25 |
9 |
3 |
21.
|
1-2 |
2-3 |
3-4 |
4-5 |
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
|
8 |
33 |
108 |
271 |
500 |
754 |
838 |
708 |
500 |
267 |
117 |
42 |
13 |
22.
|
1-2 |
2-3 |
3-4 |
4-5 |
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
|
6 |
24 |
78 |
195 |
360 |
543 |
603 |
510 |
360 |
192 |
84 |
30 |
9 |
23.
|
1-2 |
2-3 |
3-4 |
4-5 |
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
|
4 |
17 |
56 |
141 |
260 |
392 |
436 |
368 |
260 |
139 |
61 |
22 |
7 |
24.
|
1-2 |
2-3 |
3-4 |
4-5 |
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
|
6 |
25 |
81 |
203 |
375 |
566 |
628 |
531 |
375 |
200 |
88 |
31 |
9 |
25.
|
1-2 |
2-3 |
3-4 |
4-5 |
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
|
7 |
27 |
89 |
222 |
410 |
618 |
687 |
581 |
410 |
219 |
96 |
34 |
10 |
26.
|
1-2 |
2-3 |
3-4 |
4-5 |
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
|
6 |
25 |
81 |
202 |
373 |
562 |
624 |
528 |
373 |
199 |
87 |
31 |
9 |
27.
|
1-2 |
2-3 |
3-4 |
4-5 |
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
|
6 |
26 |
83 |
209 |
385 |
581 |
645 |
545 |
385 |
205 |
90 |
32 |
10 |
28.
|
1-2 |
2-3 |
3-4 |
4-5 |
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
|
7 |
28 |
91 |
228 |
420 |
634 |
704 |
595 |
420 |
224 |
98 |
35 |
11 |
29.
|
1-2 |
2-3 |
3-4 |
4-5 |
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
|
7 |
27 |
88 |
219 |
405 |
611 |
678 |
574 |
405 |
216 |
95 |
34 |
10 |
30.
|
1-2 |
2-3 |
3-4 |
4-5 |
5-6 |
6-7 |
7-8 |
8-9 |
9-10 |
10-11 |
11-12 |
12-13 |
13-14 |
|
7 |
30 |
96 |
241 |
445 |
671 |
745 |
630 |
445 |
237 |
104 |
37 |
11 |