Критерій згоди Пірсона

Припустимо, що у результаті спостережень за випадковою величиною отриманий її розподіл у виді варіаційного ряду, який характеризується частотами .

Їх сума – це об’єм сукупності . Припустимо, що емпіричним частотам відповідають теоретичні .

За міру розбіжності теоретичного і фактичного рядів частот Пірсон запропонував узяти середнє арифметичне квадратів відхилень відповідних частот, розділених на теоретичні частоти

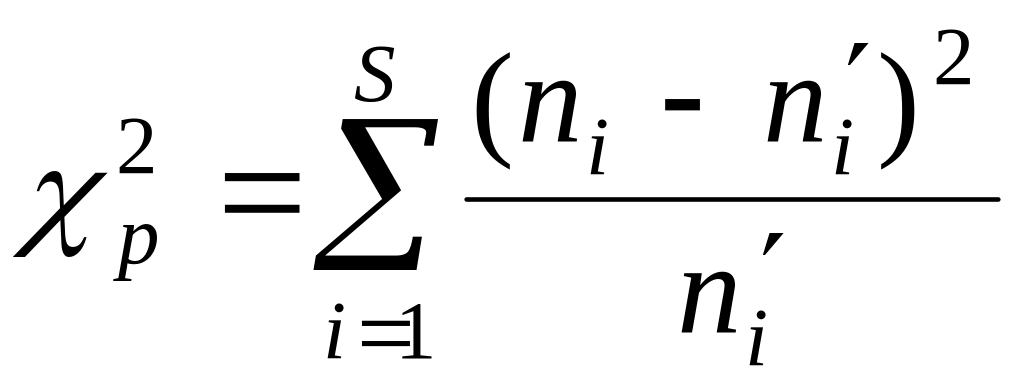(1)

Якщо всі фактичні і теоретичні частоти збігаються, то випадкова величина . В інших випадках величина (1) відрізняється від нуля, і тим більше, чим більше розбіжності між і . Із таблиці критичних значень Пірсона знаходять значення , де – це число груп (часткових інтервалів) вибірки; – число параметрів теоретичного розподілу, що було оцінено за даними вибірки, – рівень значимості, що визначає величину припустимої помилки (0,1; 0,05; 0,01). У випадку нормального розподілу =2 (математичне сподівання і дисперсія), у випадку розподілу Пуассона =1 (оцінюють один параметр ).

Правило застосування критерію Пірсона:

обчислити величину за формулою (1);
знайти по таблиці
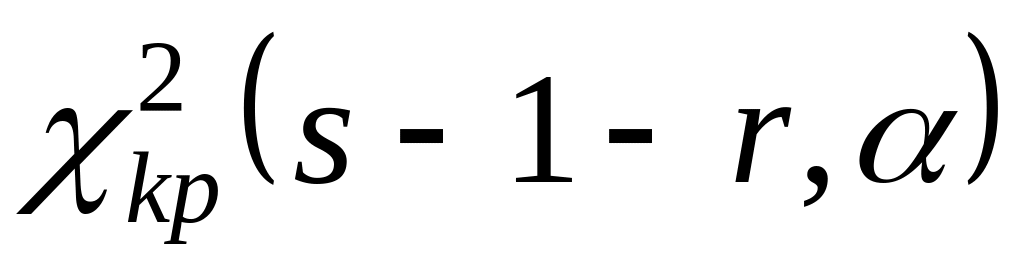
порівняти фактичне 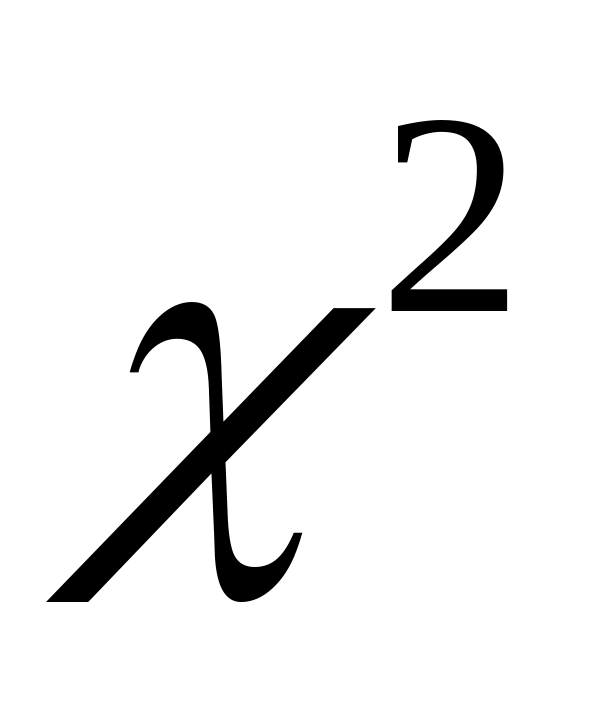і критичне значення

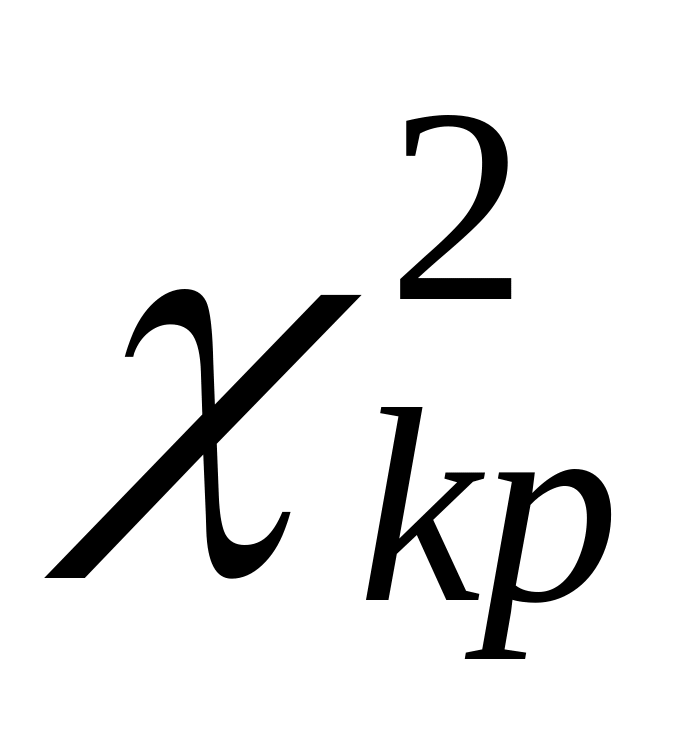
а) – немає підстав для відхилення висунутої гіпотези про теоретичний закон розподілу;

б) – гіпотезу про закон розподілу варто відхилити.

Для перевірки правильності обчислень використовують формулу

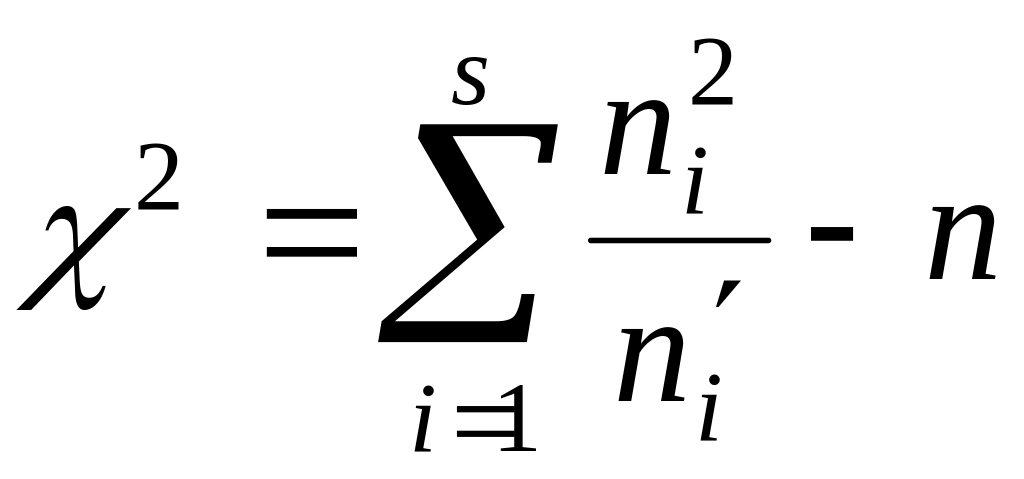Приклад.

Перевірити за критерієм Пірсона висунуту гіпотезу про нормальний розподіл сукупності.

	4	19	57	112	135	104	51	15	3
	4	18	57	111	137	105	50	15	3

Розв’язання:

Допоміжні обчислення зручно проводити в таблиці


4	4	0	0	0	16	4
19	18	1	1	0,06	361	20,06
57	57	0	0	0	3249	57
112	111	1	1	0,01	12544	113,01
135	137	-2	4	0,03	18225	133,03
104	105	-1	1	0,01	10816	103,01
51	50	1	1	0,02	2601	52,02
15	15	0	0	0	225	15
3	3	0	0	0	9	3
				0,13		500,13