Контрольные вопросы

1. Какие требования предъявляются к динамическим свойствам САУ?

2. Какими методами можно улучшить качество регулирования САУ в статике?

3. Какое влияние оказывает на динамику САУ увеличение общего коэффициента усиления разомкнутой системы?

4. Оценить качество работы замкнутой системы по л.а.х. разомкнутой системы.

5. Как определяется полоса пропускания САУ?

6. Приведите примеры жесткой и гибкой обратной связи.

7. На какие параметры качества регулирования оказывает влияние вид низкочастотного участка л.а.х.?

8. Какое влияние оказывает на динамику САУ повышение порядка астатизма?

9. Чему равна установившаяся ошибка по первой производной входного линейно нарастающего сигнала в замкнутой САУ?

10. С какой целью, как правило, вводят в САУ корректирующие звенья?

11. Возможен ли переход от одного типа корректирующего звена к эквивалентному другому типу?

12. Какими методами можно улучшить качество регулирования САУ в статике?

13. Как находится л.а.х. последовательного корректирующего устройства?

14. Как связаны между собой полоса пропускания и быстродействие САУ и чем определяются?

15. Как влияют И и Д составляющие закона регулирования на показатели качества работы?

ЛАБОРАТОРНАЯ РАБОТА № 6

ИССЛЕДОВАНИЕ СУ С ЧИСТЫ ЗАПАЗДЫВАНИЕМ

Цель работы: изучить влияние на качество работы САУ звеньев чистого запаздывания.

Экономическая система «затраты-выпуск» может быть описана следующей системой уравнений:

Q_ВЫХ = W₁(p) (μ – Q_ЗАК);

μ = η (t – τ);

η = W₂(p) ε +W₃(p) Q_ЗАК; (6.1)

η = W₂(p) ε +W₃(p) Q_ЗАК,

где η — приказы, издаваемые в момент времени t; μ — скорость выпуска готовой продукции; ε — запасы (дефицит); τ — запаздывание выпуска продукции; Q_ЗАД, Q_ВЫХ, Q_ЗАК – соответственно заданная, действительная и поступающая (требование рынка) величина запасов; W₁(p) = 1/р – передаточная функция поступления продукции на склад; W₂(p), W₃(p) – передаточные функции (законы управления), соответствующие принятию решений соответственно отделами менеджмента и маркетинга.

Требуется:

1. Составить структурную схему и разработать компьютерную модель для исследования САУ «затраты-выпуск» со звеном чистого запаздывания μ = η (t – τ);

2. Построить логарифмические частотные характеристики и определить критическое время чистого запаздывания;

3. Изменяя время чистого запаздывания t на выпуск готовой продукции в пределах (0,2¸0,8)t_кр исследовать влияние на складские запасы изменений Q_ЗАД и Q_ЗАК без учета действия отдела маркетинга (W₃ =0);

4. Подключив отдел маркетинга (компенсационная связь) проследить за изменениями складских запасов;

5. Исследовать влияние отдела менеджмента K_мн на складские запасы.

Методические указания

С точки зрения системного подхода при моделировании экономических систем необходимо сформулировать задачу, построить модель, ввести в нее необходимые параметры, получить результаты моделирования и сделать правильные выводы. Наиболее приемлемым в этом случае будет применение имитационных моделей на ЭВМ, допускающих многовариантность расчетов при неполной и недостаточной достоверности информации, а также невозможность или нежелательность экспериментальных исследований.

Уравнениям САУ «затраты-выпуск» (6.1) соответствует структурная схема, представленная на рис. 6.1.

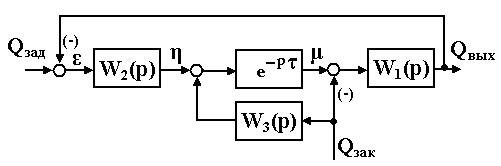
Рис.6.1

Приведенная система регулирования запасов с точки зрения имитационного моделирования интересна тем, что регулирование запасов не является тривиальной задачей. И здесь важно найти такую функцию реального принятия решения W₃(p) (отдел маркетинга), связанной с новыми поступлениями заказов, чтобы стабилизация их была совершенной (оптимальной). В структурной схеме рис. 6.1 менеджмент участвует в замкнутом контуре системы регулирования запасов и от его действий (законов управления) также зависит оптимизация складских запасов.

Большие запасы порождают затраты по уплате процентов, а также, возможно, издержки физического обесценивания при хранении, складские затраты и т.д. С другой стороны, нехватка запасов (избыточные отрицательные запасы) вызывает затраты в смысле задержки в выполнении заказов, а следовательно, недоброжелательное отношение заказчиков. Разумно предположить (потребовать при моделировании), что издержки производства определенного количества продукции за некоторый промежуток времени будут минимальными при постоянном выпуске продукции.

В лабораторной работе следует принять передаточную функцию реального менеджмента W₂(p) = K_мн (p+χ), где параметры K_мн и χ берутся из таблиц в соответствии с вариантом задания. Передаточная функция маркетинга может быть принята в виде W₃(p) = К_мк.

Рассчитать критическое время чистого запаздывания можно различными способами. Первоначально определяется критическая частота или частота среза. Для этого необходимо найти

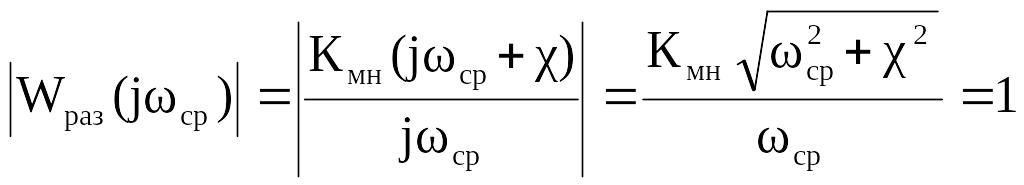. Откуда .

Далее находится запас по фазе или критический угол

. Тогда .

В отчете по лабораторной работе должны быть представлены частотные характеристики, расчет критического времени чистого запаздывания, переходные характеристики в соответствии с исследованиями, указанными в п.п.3 ÷ 5. Представить анализ влияния на параметры складских запасов t, K_мн и К_мк. При исследовании влияния K_мн и К_мк на складские запасы следует соответственно отключать или Q_ЗАД, или Q_ЗАК, чтобы правильно сделать выводы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что такое критическая частота и как она связана с частотой среза системы?

2. Какой вид имеет годограф звена чистого запаздывания?

3. Как влияет на модуль разомкнутой системы введение звена чистого запаздывания?

4. Как влияет на запас по фазе САУ введение звена чистого запаздывания?

5. Как влияет расположение звена чистого запаздывания на показатели качества САУ от изменения Q_ЗАК и Q_ЗАД?

ЛАБОРАТОРНАЯ РАБОТА №7

ИССЛЕДОВАНИЕ НЕЛИНЕЙНОЙ САУ

Цель работы: исследование влияния параметров нелинейной и линейной части САУ на амплитуду и частоту автоколебаний.

В линейную САУ следящего электропривода с пропорциональным регулированием (лаб. работа №4) вводятся последовательно нелинейные звенья, представленные на Рис.7.1.

Типовые нелинейности

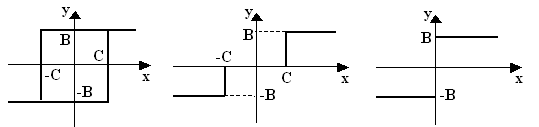
а) б) в)

Рис.7.1

Параметры В и С нелинейностей заданы в таблице № 2. Для линейной части взять К_раз нескорректированной САУ.

Требуется:

1. Методом гармонической линеаризации определить возможные частоту и амплитуду автоколебаний для каждого типа нелинейностей и для различных К_раз;

2. Составить математическую модель с применением пакета SyAn отработки управляющего воздействия нелинейной САУ j_вх(t)=1(t) с типовыми нелинейностями, представленными на Рис.7.1;

3. Получить переходные характеристики j_вых(t) при ступенчатом входном воздействии. Оценить время переходного процесса, а при возникновении автоколебаний найти их амплитуду и частоту. Сравнить их с теоретически найденными в п.1. и построить фазовый портрет;

4. Исследовать влияние на параметры автоколебаний изменения параметра В нелинейности Рис.7.1,в;

5. Исследовать влияние на параметры автоколебаний изменения коэффициента усиления линейной части САУ с нелинейностью Рис.7.1,а.