
Методические указания
В таблице №3 указана передаточная функция (отношение выхода ко входу), которая должна быть выведена в соответствии с вариантом задания, а в таблице №2 приведены параметры Zj схемы рис.1.1.
При составлении математического описания какой-либо системы основным условием является знание законов функционирования системы (знание физических, технических и других принципов работы системы и ее элементов, знание законов информационного взаимодействия компонентов и т.п.).
Так как в качестве исследуемой системы в лабораторной работе Вам предлагается простейшая электрическая цепь, прежде всего Вам необходимо вспомнить основные законы электротехники. Естественно, применять Вы можете те законы, методы и правила, которые Вам больше нравятся или которые Вам понятнее других. Учитывая это обстоятельство, можно сразу отметить, что не существует какого-то стандартного, единого пути составления математического описания системы и поэтому правильное описание может быть получено разными способами, однако все эти описания в конечном итоге можно свести к нескольким типовым формам, что и требуется при выполнении данной работы. Возможно использование метода контурных токов, узловых напряжений или операторного метода.
Рассмотрим возможную процедуру получения математической модели (передаточной функции) простейшего пассивного LRC – фильтра, электрическая схема которого показана на рис.1.2, с использованием операторного метода.
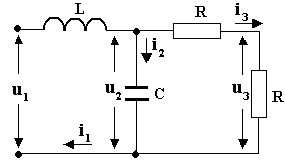
Рис. 1.2
Найдем передаточную функцию, если входной величиной пусть будет u1(t), а выходной – i3(t), т.е.
![]() (1.1)
(1.1)
где I3(p) и U1(p) изображения соответственно выходной и входной величин; p = d/dt – оператор Лапласа.
Найдем суммарное сопротивления фильтра
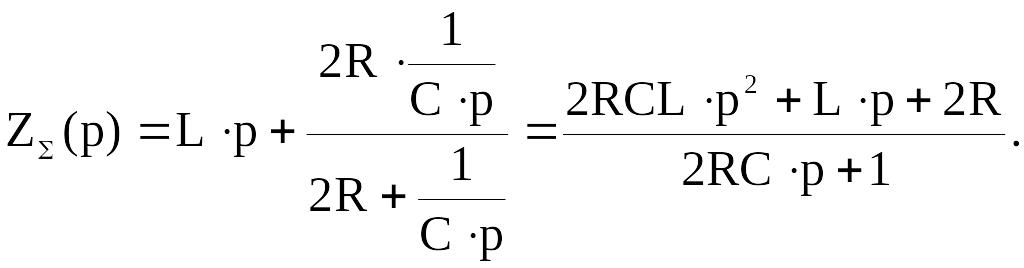 (1.2)
(1.2)
Ток I3(p) можно найти
![]() (1.3)
(1.3)
Кроме того, справедливо соотношение
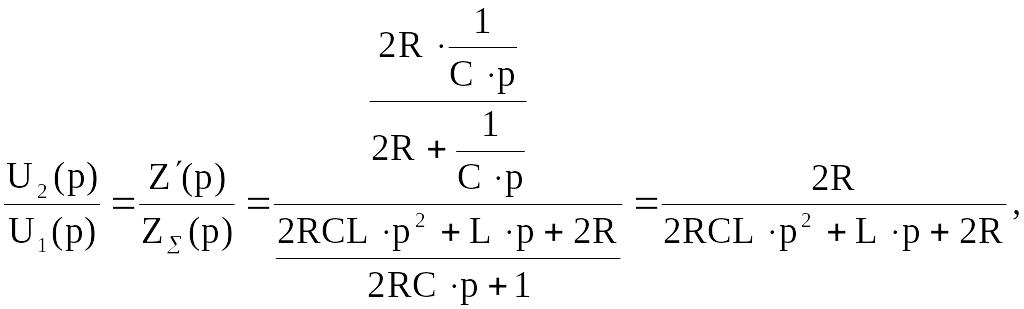 (1.4)
(1.4)
где (рис.1.2)
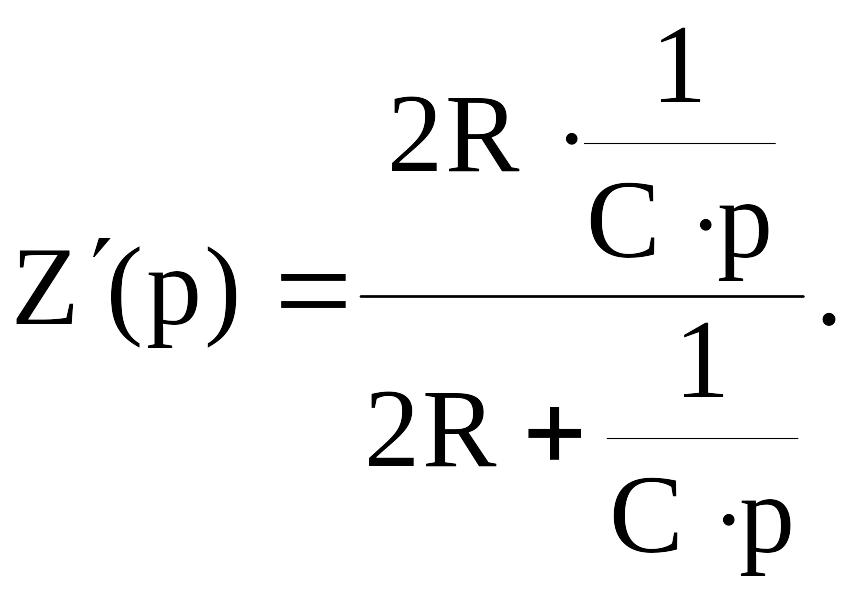
Подставляя выражение для U2(p) из (1.4) в (1.3), получим
 (1.5)
(1.5)
Тогда передаточная функция (1.1) будет иметь вид
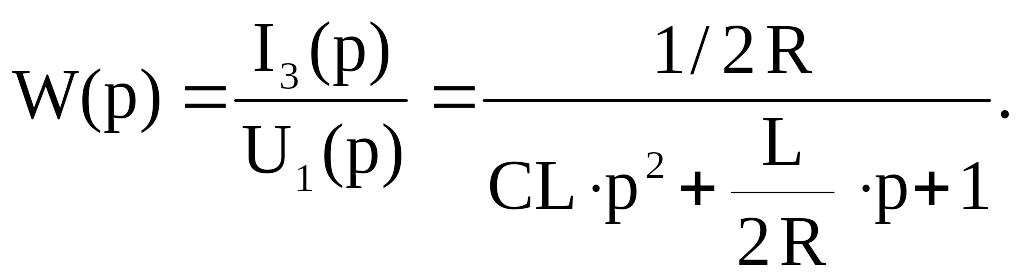 (1.6)
(1.6)
Таким образом, как видно из выражения (1.6), математическим описанием простейшей системы рис. 1.2 в зависимости от параметров является передаточная функция либо колебательного звена, либо апериодического второго порядка.
Годограф передаточной функции (а.ф.х.) строится в диапазоне частот ¥ ³ w ³ 0 в соответствии с выражением (после подстановки p=jw в передаточную функцию (1.6)):
W(jw)= P(w)+jQ(w) – а.ф.х. (годограф);
где P(w)- действительная часть; Q(w) – мнимая часть;
![]() – а.ч.х. (модуль);
– а.ч.х. (модуль);
20 lq A(w) – л.а.х.;
j(w) = arctg (Q(w)/P(w)) – л.ф.х. (фаза).
Частотная передаточная функция W(jw) может быть представлена на комплексной плоскости. Графическое отображение для всех частот спектра отношений выходного сигнала САУ к входному, представленных в комплексной форме, будет представлять собой амплитудно-фазовую частотную характеристику (а.ф.х.) или годограф Найквиста. Величина отрезка от начала координат до каждой точки годографа показывает, во сколько раз на данной частоте выходной сигнал отличается от входного (а.ф.х.), а сдвиг фазы между сигналами определяется углом до упомянутого отрезка (ф.ч.х.). При этом отрицательный фазовый сдвиг представляется вращением вектора на комплексной плоскости по часовой стрелке относительно вещественной положительной оси, а положительный фазовый сдвиг представляется вращением против часовой стрелки.
Для упрощения графического
представления частотных характеристик,
а также для облегчения анализа процессов
в частотных областях используются
логарифмические частотные характеристики:
логарифмическая амплитудная частотная
характеристика (л.а.х.) и логарифмическая
фазовая частотная характеристика
(л.ф.х.). При построении логарифмических
характеристик на шкале частот вместо
w
откладывается lgw
и единицей измерения является декада.
Декадой называется интервал частот,
соответствующий изменению частоты
в 10 раз. При построении л.а.х. на оси
ординат единицей измерения является
децибел [дБ], который
представляет собой соотношение L=20
lg А(w).
Один децибел представляет собой
увеличение амплитуды выхода в
![]() раз. Верхняя полуплоскость л.а.х.
соответствует значениям А >
1 (усиление амплитуды), а нижняя
полуплоскость - значениям А <
1 (ослабление амплитуды). Точка пересечения
л.а.х. с осью абсцисс соответствует
частоте среза wср,
при которой амплитуда выходного сигнала
равна входной.
раз. Верхняя полуплоскость л.а.х.
соответствует значениям А >
1 (усиление амплитуды), а нижняя
полуплоскость - значениям А <
1 (ослабление амплитуды). Точка пересечения
л.а.х. с осью абсцисс соответствует
частоте среза wср,
при которой амплитуда выходного сигнала
равна входной.
Для л.ф.х. по оси частот откладывается логарифмический масштаб, а для углов - натуральный масштаб. На практике логарифмические частотные характеристики строятся на совмещённой системе координат как показано на рис. 1.3.
Главным достоинством логарифмических частотных характеристик является возможность построения их во многих случаях практически без вычислительной работы. Особенно удобно использовать логарифмические частотные характеристики при анализе всей системы, когда результирующая передаточная функция после разложения на множители приводится к виду:
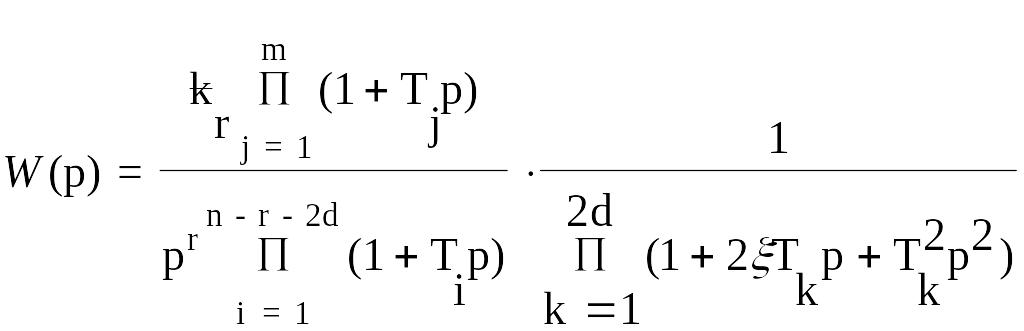 ,
(1.7)
,
(1.7)
т.е. передаточную функцию любой САУ в общем случае можно представить как произведение передаточных функций следующего вида:
![]()
где Kr, r, T, x - постоянные величины, причём Kr >0, r >0, T >0, 0< x <1.
Система координат для логарифмических характеристик
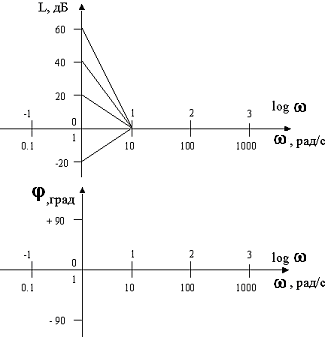
Рис. 1.3
В этом случае построение л.а.х. производится по выражению
L(w)=20lgA(w)=20lg|W(jw)|=20lgk+
20lg(1/wr)+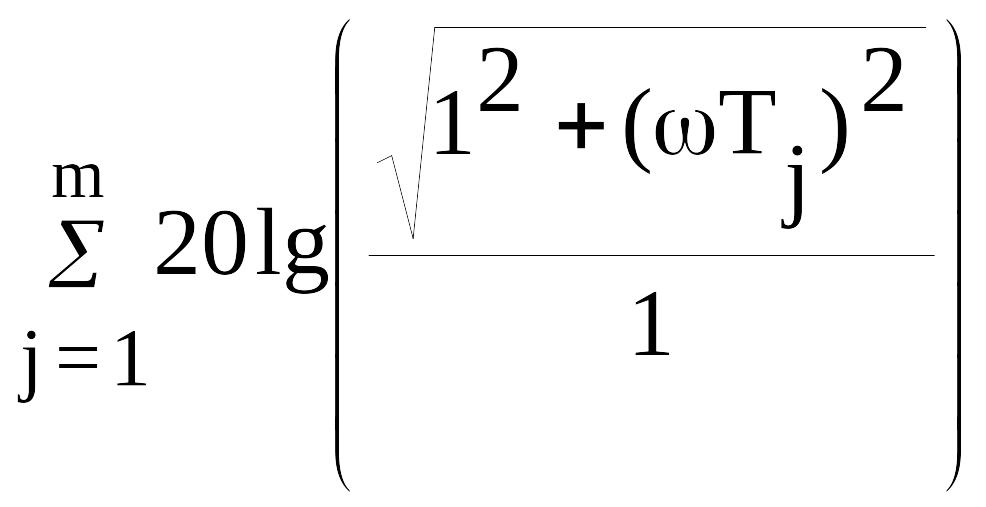 +
+
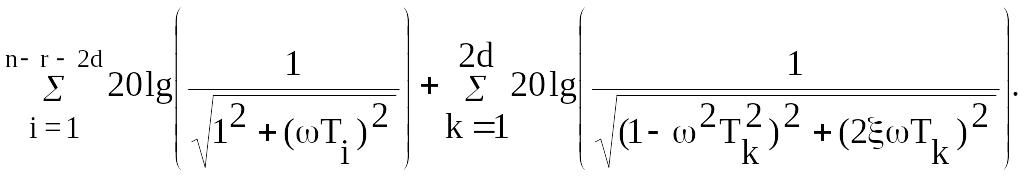
Построение л.ф.х. производится по выражению
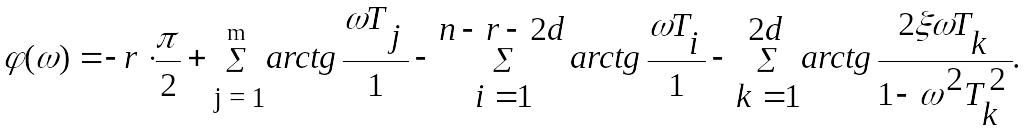
Таким образом, результирующая л.а.х. определяется суммированием л.а.х. составляющих типовых звеньев, а результирующая л.ф.х. - соответственно суммированием л.ф.х. составляющих типовых звеньев.
П р и м е р. Построить л.а.х. и л.ф.х. системы, описываемой передаточной функцией
W(p)=100/(0.1p+1)(0.01p+1).
Р е ш е н и е . Представим передаточную функцию в виде произведения элементарных звеньев
![]()
Низкочастотный участок л.а.х. пойдет с наклоном 0 дБ/дек на уровне 20lg 100 = 40дБ. Частоты сопряжения для апериодических составляющих будут соответственно w1=1/0.1=10 и w2=1/0.01=100. Фазочастотная характеристика строится в соответствии с уравнением j(w)= - arctg 0.1 w - arctg 0.01 w. Ниже на рис. 1.4 представлены графики л.а.х. и л.ф.х., соответствующие заданной передаточной функции.
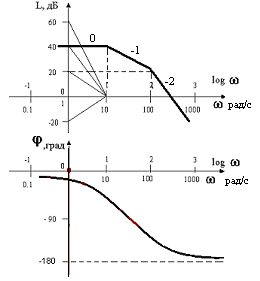
Рис. 1.4.
В том случае, когда работа отдельного устройства или системы в целом не может быть точно описана дифференциальными уравнениями, возможно экспериментальное определение динамических характеристик. Рекомендуется схему предварительно начертить на бумаге и на этом чертеже расставить номинальные значения параметров компонентов.
Анализ схемы по переменному току
заключается в получении амплитудно- и
фазочастотных характеристик. Для этого
необходимо поместить в рабочую область
три прибора: генератор сигналов;
графопостроитель частотных характеристик;
двухлучевой осциллограф. После этого
нужно подключить приборы к схеме так,
как показано на рис.1.5 ( для определения
![]() .
.
Схема подключения измерительных приборов
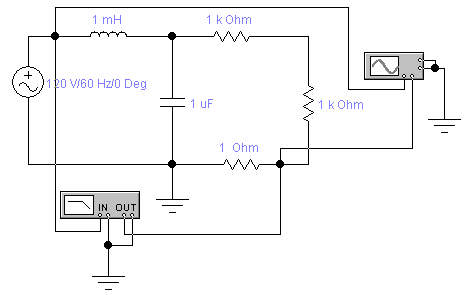
Рис. 1.5
Рекомендуется устанавливать цветные провода, идущие к осциллографу от входа и от выхода схемы (тогда цвет луча на экране будет совпадать с цветом провода). Цвет устанавливается так: указать на провод и дважды нажать левую клавишу мыши; в открывшемся окне выбрать цвет.
Для настройки приборов сначала их нужно “развернуть”, дважды нажав левую кнопку мыши, указывая на выделенный в рабочем окне прибор.
Генератор для снятия частотных характеристик специально настраивать не требуется, т.к. его параметры графопостроителем игнорируются. Если в процессе анализа используется осциллограф, то на генераторе необходимо установить вид сигнала, а затем частоту и амплитуду сигнала.
Настройка графопостроителя заключается в следующем:
-для построения амплитудно-частотной характеристики выбрать “magnitude”;
-для построения фазочастотной характеристики нужно выбрать “phase”;
-на горизонтальной оси нужно выбрать логарифмический масштаб “LOG” (тогда на вертикальной оси будет откладываться коэффициент передачи в децибелах, а по горизонтальной оси - частота в логарифмическом масштабе);
-установить начальные значения координат (I-initial) и конечные значения (F-final),которые, по Вашему мнению, соответствуют свойствам Вашей схемы (не забудьте установить размерность частоты Hz или kHz).
При настройке осциллографа:
-установить временной масштаб развертки по оси Х (TIME BASE);
-установить режим работы Y/T и AUTO;
-установить чувствительность канала А и канала В (например, 1V/DIV- 1Вольт на деление);
-установить открытый вход DC.
При необходимости можно распечатать схему с подключенными приборами (см. рис.1.5) и сами приборы (осциллограф с осциллограммами, графопостроитель с частотными характеристиками и т.п.) с помощью команды PRINT из меню FILE.
Пример результатов анализа для схемы RLC - фильтра рис.1.2. показан на рис. 1.6-1.8.
Генератор сигналов
Рис.1.6
Двухлучевой осциллограф

Рис.1.7
Графопостроитель с АЧХ
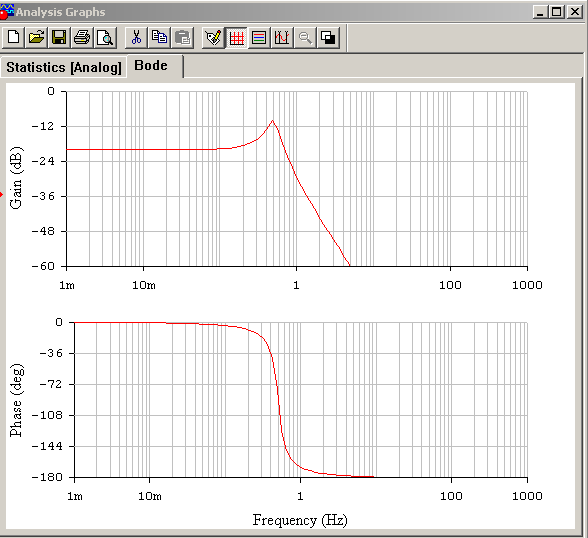
Рис. 1.8
В отчете по лабораторной работе привести цель работы, схему системы с номиналами, расчеты и графики по п.1, принципиальную схему модели, результаты моделирования (л.а.х. и л.ф.х., построенные графопостроителем, не менее 6 комплектов экспериментальных синусоид) и выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
При решении каких проблем применяют частотные характеристики (ЧХ)?
Что такое модуль и фаза ЧХ ?
Что такое частота среза wср звена и системы ?
Как по передаточной функции получить ЧХ ?
Каково назначение математического описания систем?
Что такое динамика системы? Чем отличается математическое описание динамики системы от описания ее статики?
Как перейти от дифференциального уравнения к операторному?
Дайте определение передаточной функции.
Как по дифференциальному уравнению звена найти его передаточную функцию?
ЛАБОРАТОРНАЯ РАБОТА №2
ВЕКТОРНО-МАТРИЧНЫЙ АНАЛИЗ СИСТЕМ УПРАВЛЕНИЯ
Цель работы: приобретение навыков составления структурных схем в соответствии с уравнениями состояния и математического моделирования с применением ЭВМ.
В лабораторной работе №1 составлена передаточная функция RLC – контура.
Требуется:
Разработать блок-схему для получения производных нужного порядка и написать уравнения состояния в нормальной форме (этот пункт должен быть выполнен заранее, до прихода на лабораторные занятия)
 ; (2.1)
; (2.1)
С помощью системы компьютерного моделирования SyAn смоделировать уравнения переменных состояния п. 1 (модель должна содержать только элементы сравнения, идеальные интеграторы и элементы связи);
Получить передаточную функцию, а.ф.х. (годограф), л.а.х. и л.ф.х. Сравнить их с полученными в лабораторной работе №1;
По заданию преподавателя исследовать влияние какого либо параметра передаточной функции на частотные характеристики;
Построить переходный процесс и оценить его параметры.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
В общем случае обыкновенных линейных систем, описываемых системой дифференциальных уравнений в нормальной форме, рассматриваемая система может быть определена следующей векторно-матричной формой (2.1):
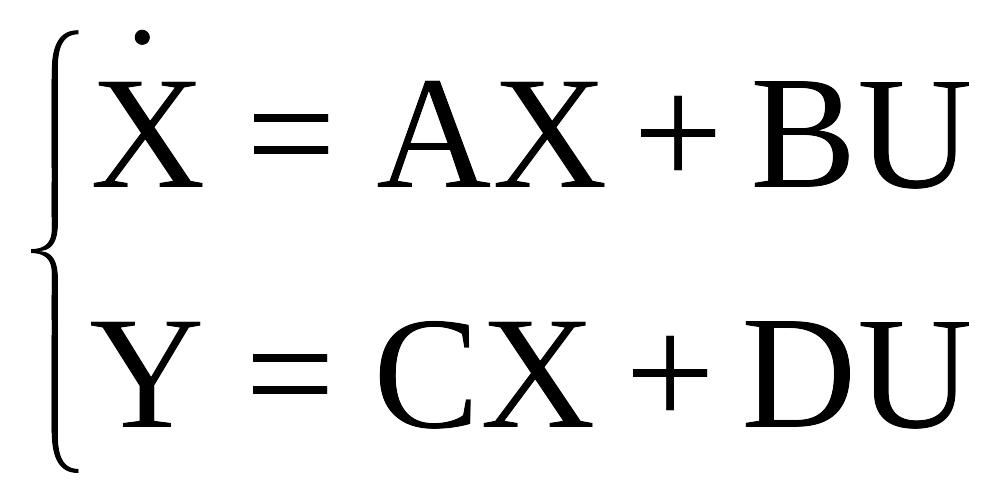 ,
,
где: X - вектор состояния системы; Y - вектор выходных управляемых величин; А, В, С, D - матрицы системы; U - вектор внешних воздействий (задающих и возмущающих), а именно:
 ,
,
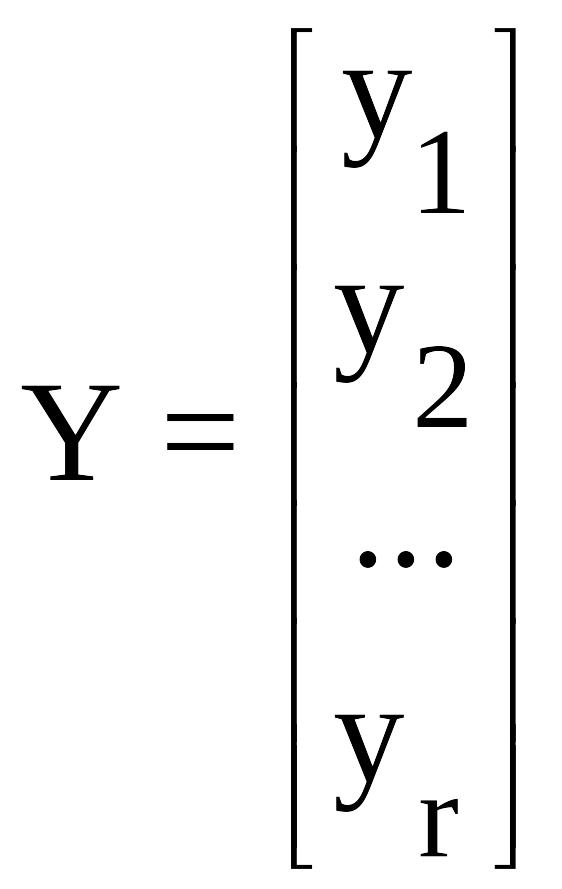 ,
,
 .
.
Система уравнений является стандартным описанием систем управления в пространстве состояний. Уравнения несут большой объем информации о динамических свойствах системы с m входами и r выходами при t0 £ t £ T. Первое уравнение определяет динамические характеристики системы и представляет собой компактную запись системы n линейных дифференциальных уравнений, разрешенных относительно производных первого порядка (нормальная форма Коши)
![]() при i=1,2, ... ,n,
при i=1,2, ... ,n,
где aij и bij - постоянные коэффициенты.
Второе уравнение является уравнением выхода системы и представляет собой компактную запись системы r линейных алгебраических уравнений
![]() при i=1,2, ... ,r,
при i=1,2, ... ,r,
где cij и dij - постоянные коэффициенты.
В стандартной форме описания
 -
матрица системы;
-
матрица системы;
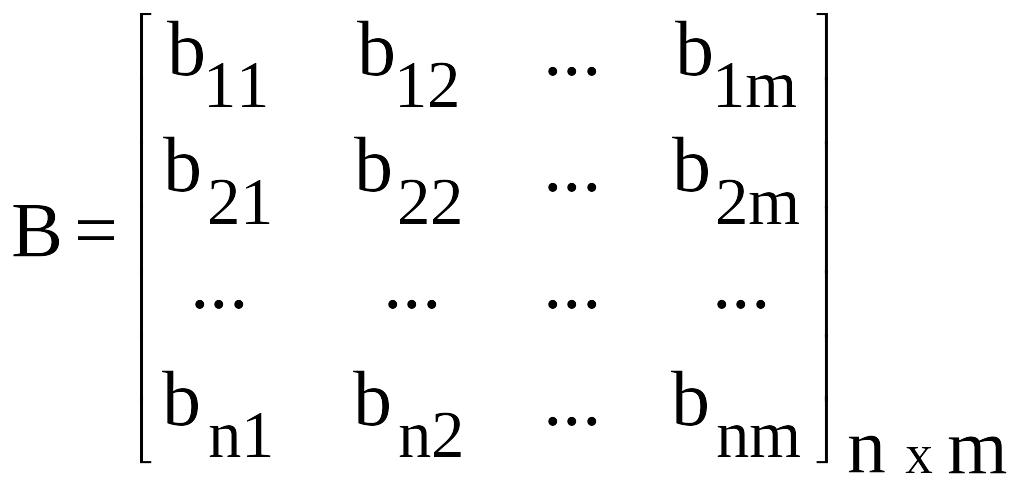 -
матрица управления;
-
матрица управления;
 -
матрица наблюдения;
-
матрица наблюдения;
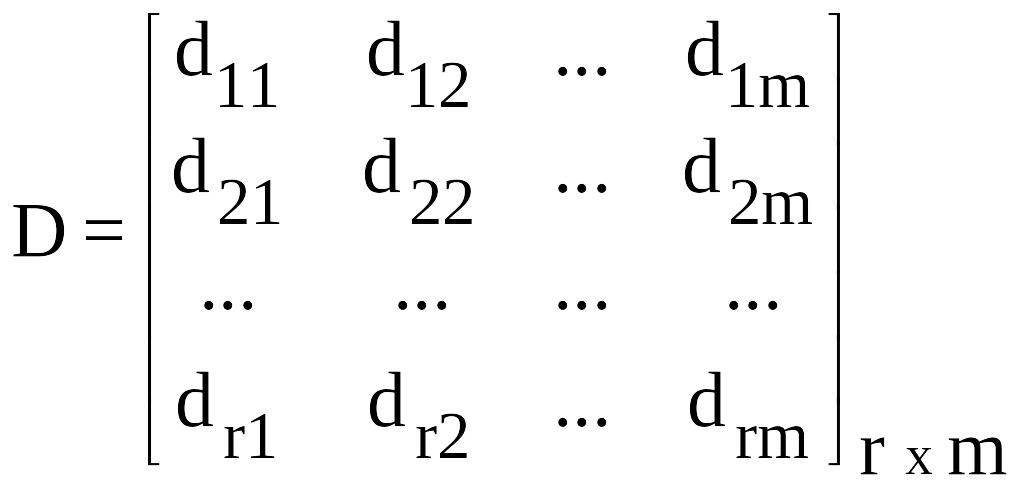 -
матрица связи.
-
матрица связи.
Матрица системы A, элементы которой определяются структурной схемой системы и значениями ее параметров, характеризует динамические свойства системы, ее свободное движение. Матрица управления B характеризует влияние внешних воздействий на переменные состояния системы, т.е. определяет чувствительность системы к внешним воздействиям (задающим и возмущающим). Матрица наблюдения C характеризует связь выходной величины системы с вектором состояния. Матрица связи D устанавливает связь выходной величины системы с внешним воздействием. Таким образом, четверка матриц A, B, C, D полностью определяет систему управления.
Матричные методы дают возможность обращаться с n уравнениями подобно тому, как это делается с одним уравнением.
На рис.2.1 показана структурная схема системы управления, соответствующая стандартной форме описания систем в пространстве состояний; жирные линии на рисунке характеризуют векторные связи. Следует иметь в виду, что выбор переменных состояния это неоднозначная операция. Значение начального состояния X(t0) и входного воздействия U(t) достаточны для того, чтобы однозначно и единственным образом найти выходную величину Y(t) на интервале времени t0 £ t £ T, т.е. определить значения Y(t) в текущий момент и предсказать поведение ее в будущем.
Уравнения переменных состояния представляют собой наиболее полное математическое описание динамики системы с несколькими входами и выходами и позволяют легко перейти к модели реальной системы и получить решение с применением вычислительной техники. Рассмотрим методику составления векторно-матричных дифференциальных уравнений для систем с одним входом и одним выходом на конкретном примере.
Структурная схема системы в векторной форме
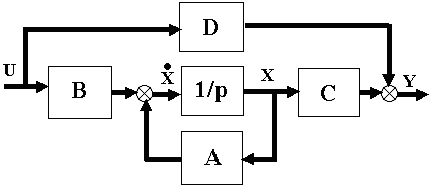
ò - блок интеграторов; A,B,C,D - блоки матричных усилителей
Рис.2.1
Составление детализированной структурной схемы по уравнениям состояния (2.1) целесообразно вести в следующей последовательности:
изобразить n идеальных интеграторов с передаточными функциями 1/p, где n - порядок системы. Обратить внимание на то обстоятельство, что выходной величиной интегратора является переменная состояния xi, а входной - ее производная d xi /dt;
используя блоки суммирования и масштабирования, организовать связи между входами и выходами интеграторов в соответствии с первым уравнением (2.1);
используя блоки суммирования и масштабирования, организовать связи между переменными состояния в соответствии со вторым уравнением (2.1).
Составив структурную схему в переменных состояния и используя правила преобразований, легко составить по ней передаточные функции по любым координатам и управляющим воздействиям. Если работа системы уже описана передаточной функцией, то в этом случае нет необходимости описывать ее заново через переменные состояния, тогда можно просто преобразовать передаточную функцию в уравнения состояния. Структурная схема системы в переменных состояния может быть составлена по передаточной функции тремя способами: методом прямого программирования, методом параллельного программирования и методом последовательно программирования.
Метод прямого программирования позволяет представить систему уравнений состояния в нормальной канонической форме по известной передаточной функции звена или системы с одним входом и одним выходом. Для примера возьмем систему второго порядка, передаточная функция которой в общем виде
![]() ,
(2.2)
,
(2.2)
Передаточной функции (2.2) соответствует дифференциальное уравнение
![]()
Разрешив его относительно старшей производной по y(t), получим
![]()
Решение в этом случае может быть получено методом понижения порядка. Для этого последовательно необходимо поставить n-интеграторов, где n – порядок звена или системы.
Можно составить структурную схему, состоящую из двух последовательно соединенных звеньев, непосредственно по (2.2). На рис.2.2. изображена структурная схема, соответствующая передаточной функции (2.3).
![]() (2.3)
(2.3)
Общая структурная схема для звена второго порядка
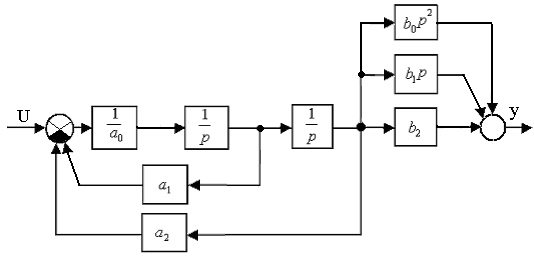
Рис.2.2
Структурная схема, изображенная на рис.2.2., включает в себя идеальные дифференцирующие звенья. С помощью структурных преобразований можно избавиться от них и представить структурную схему в виде рис.2.3.
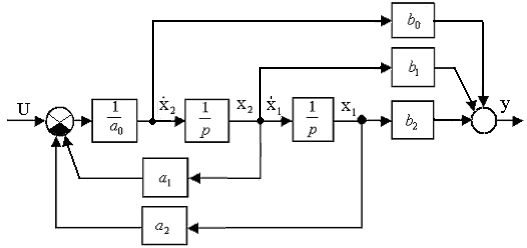
Рис.2.3
Ввиду того, что имеется множество эквивалентных способов представления уравнений состояния системы, можно выбрать из них "наилучшие", позволяющие снизить трудоемкость вычислений при решении конкретной задачи. Такие формы записи уравнений называются каноническими. Поскольку может быть много различных приложений, известно и много канонических форм. Наиболее распространенные из них: блочно-диагональная форма Жордана; матрица Фробениуса. Если модель можно разбить на ряд элементарных (описываются уравнениями первого порядка), параллельно включенных блоков, то целесообразно применить форму Жордана (корни характеристического уравнения располагаются на диагонали). На рис.2.3 приведен пример представления модели матрицей Фробениуса (2.4), когда характеристическое уравнение располагается в последней строке.
В соответствии с векторно-матричным уравнением (2.1) скалярные уравнения имеют вид:
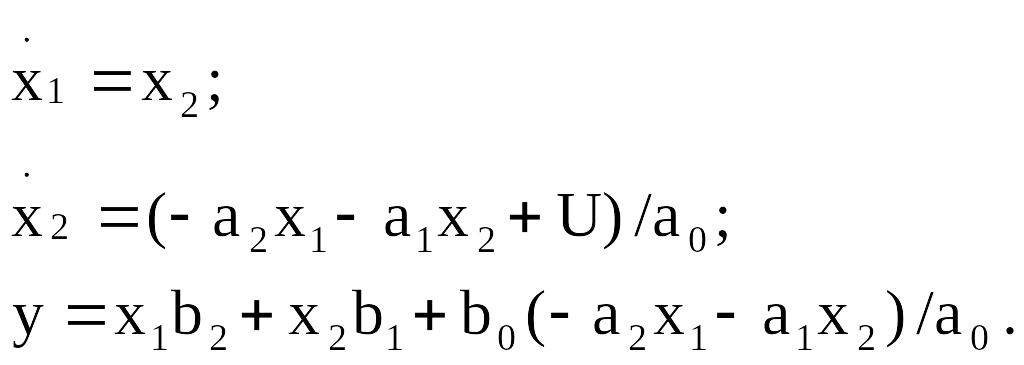 (2.4)
(2.4)
На рис.2.3 приведен пример представления модели матрицей Фробениуса (2.5), когда характеристическое уравнение располагается в последней строке.
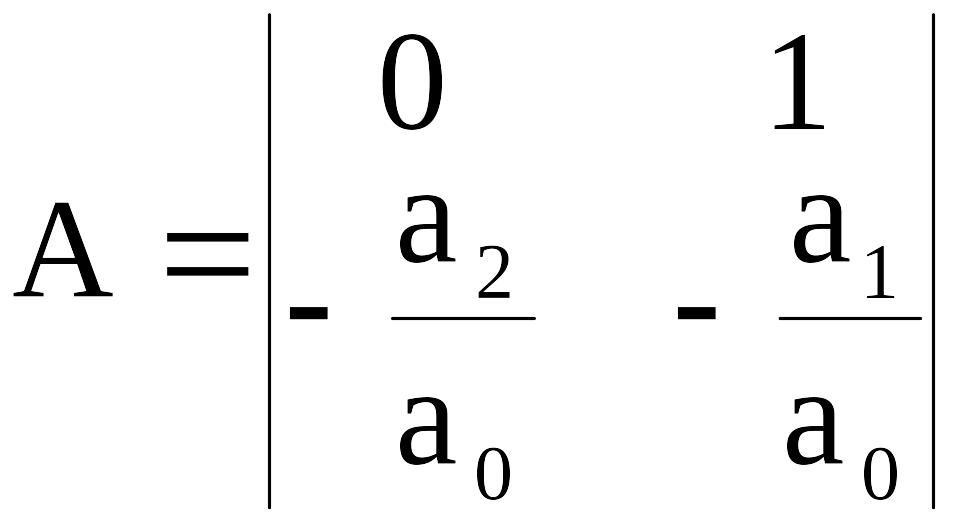 (2.5)
(2.5)
Расчетная структурная схема модели не должна иметь алгебраических петель. В противном случае интегрирование не осуществимо. На рис.2.4,а представлена структурная схема системы, у которой наблюдается алгебраическая петля (выделена жирной линией).
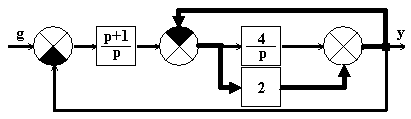
а)

б)
Рис.2.4
Чтобы расчет был возможен, необходимо предварительно преобразовать приведенную структуру для исключения алгебраической петли, как показано на рис.2.4,б.
В лабораторной работе при составлении структурной схемы в пакете SyAn (рис.2.3) и написании уравнений состояния (2.4) следует исключить блоки с коэффициентами, отсутствующими в конкретной (в соответствии с Вашим выводом) передаточной функции (2.2).
На рис.2.5 представлена обобщенная модель для исследования звена с передаточной функцией (2.2), полученная с помощью пакета SyAn.
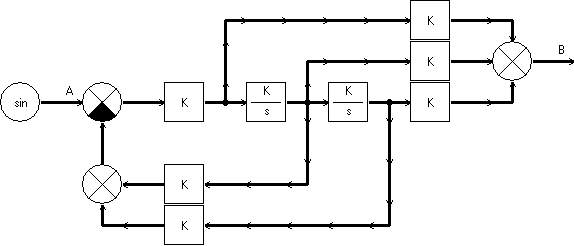
Рис.2.5
В отчете к лабораторной работе целесообразно асимптотическую л.а.х. провести на л.а.х., полученной в пакете SyAn, с указанием сопрягающих частот Вашей передаточной функции звена.
Для получения
переходного процесса необходимо в
модели рис.2.5 вместо блока
![]() поставить блок
поставить блок
![]() .
Оценить по переходному процессу время
и величину установившегося значения.
Воспользовавшись предельным свойством
преобразования Лапласа найти по Вашей
передаточной функции установившееся
значение при подаче на вход сигнала
1(t).
.
Оценить по переходному процессу время
и величину установившегося значения.
Воспользовавшись предельным свойством
преобразования Лапласа найти по Вашей
передаточной функции установившееся
значение при подаче на вход сигнала
1(t).
![]() КОНТРОЛЬНЫЕ
ВОПРОСЫ
КОНТРОЛЬНЫЕ
ВОПРОСЫ
Что представляет собой структурная схема системы управления?
Каким образом экспериментальным путем можно оценить качество работы системы?
Какова роль моделирования систем управления?
Что такое состояние, пространство состояний, вектор состояния?
Запишите стандартную форму уравнений в пространстве состояний. Поясните физический смысл уравнений.
От каких параметров передаточной функции зависят элементы матрицы системы управления?
Какова структура решения уравнений переменных состояния?
Перечислите характеристики систем в пространстве состояний.
Дайте понятие управляемости и наблюдаемости систем и критерии их проверки.
Запишите характеристический определитель матрицы A.
Что представляет собой нормальная форма уравнений в пространстве состояний? Как ее получить?
ЛАБОРАТОРНАЯ РАБОТА №3
ИССЛЕДОВАНИЕ ПИД-РЕГУЛЯТОРА
Цель работы: изучение методики настройки ПИД-регулятора, обеспечивающей получение требуемых динамических характеристик системы на основе использования пакета SyAn.
Дана следящая система с объектом второго порядка и регулятором, представленная на рис.3.1. В соответствии с вариантом задания параметров системы требуется:
Найти передаточные функции разомкнутых САУ в общем виде с различными регуляторами. Определить статические ошибки регулирования по управляющему воздействию;
Рассчитать параметры регуляторов, обеспечивающих уменьшение перерегулирования, сокращение времени переходного процесса и устранение или снижение статической ошибки;
Построить асимптотические л.а.х. и л.ф.х. разомкнутых систем с различными регуляторами. Определить частоту среза, запасы устойчивости по модулю и фазе;
Экспериментально получить переходные процессы с использованием пакета прикладных программ и дать заключение о качестве работы системы.

Рис.3.1
