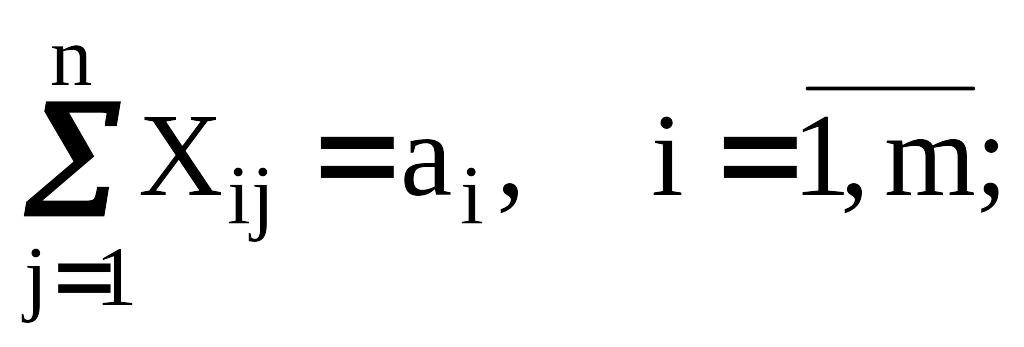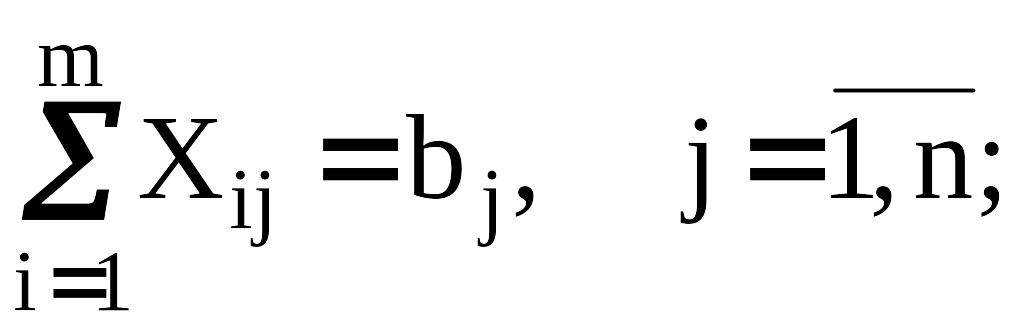- •Двусторонние шпоры по файзу
- •Печатай прямо этот файл
- •Теория принятия решений [3, 4]
- •1. Классы задач принятия решений, системный анализ и характеристика его этапов.
- •2. Графы и показатели эффективности смо с простейшими потоками.
- •6. Замкнутые смо.
- •3. Принятие решений в условиях риска, неопределенности и конфликты.
- •4. Основы линейного программирования. Область применения. Постановка задачи
- •Каноническая форма задач лп
- •Стандартная форма задачи лп
- •Основные понятия лп. Свойства задач лп
- •Методы решения задач лп
- •Симплекс-метод. Характеристика метода
- •М одифицированный алгоритм симплекс-метода
- •Модели управления транспортными потоками.
- •Простейшая транспортная задача (т-задача)
- •Транспортная задача с ограниченными пропускными способностями (Td - задача)
- •Задачи с неоднородным грузом
- •Многоиндексные задачи
- •Транспортные задачи по критерию времени
- •6. Оптимизация транспортных потоков. Метод потенциалов
- •Построение начального плана перевозок
- •Правило северо-западного угла
- •Переход от одного плана перевозок к другому
- •Признак оптимальности
- •Алгоритм метода потенциалов
- •7. Методы управления проектом.
- •8. Двойственность задач оптимизации. Двойственность задач лп
- •Интерпретация двойственной задачи
- •Запись двойственной задачи в общем случае
- •Теоремы двойственности
- •Двойственный симплекс-метод
- •9. Декомпозиция задач планирования большой размерности.
- •Метод декомпозиции Данцига - Вулфа
- •10. Методы определения целочисленных решений.
- •Метод отсечений
- •Метод ветвей и границ
- •Аддитивный алгоритм
- •11. Основы динамического программирования. Достоинства и недостатки метода.
- •Работа метода дп
- •Функциональное уравнение дп
- •Многомерные задачи динамического программирования
- •Снижение размерности с помощью множителей Лагранжа
- •12. Оптимизация надежности технических систем, систем распределения ресурсов.
- •4.2.3. Сбалансированная транспортная задача
- •13. Классы задач нелинейного программирования и методы их решения. Х арактеристика задач
- •Условия оптимальности
- •Методы решения задач нп
- •14. Задачи нелинейного программирования, сводящиеся к линейным. Квадратичное программирование
- •Сепарабельное программирование (сп)
- •Задачи дробно-линейного программирования
- •15. Классификация и характеристика методов «спуска».
- •Методы одномерной минимизации. Метод деления шага пополам
- •Квадратичная аппроксимация
- •Метод деления интервала пополам
- •Метод золотого сечения
- •Метод Фибоначчи
- •Метод первого порядка
- •Методы второго порядка
- •Многомерный поиск безусловного минимума Метод Гаусса-Зейделя (покоординатного спуска)
- •Метод Хука-Дживса (метод конфигураций)
- •Симплексный метод
- •Градиентные методы
- •Метод Ньютона
- •М етоды сопряженных направлений
- •Методы условной оптимизации
- •Метод проектирования градиента
- •Метод штрафных функций
- •Метод барьерных функций
- •16. Методы случайного поиска и генетические алгоритмы.
- •8.8.7. Методы случайного поиска
- •Алгоритм с возвратом при неудачном шаге
- •Алгоритм с обратным шагом
- •Алгоритм наилучшей пробы
- •Алгоритм статистического градиента
- •8.8.8. Генетические алгоритмы
- •17. Особенности принятия решений при многих критериях.
- •18. Методы свертки и целевого программирования в принятии решений по многим критериям.
- •10.2.1.4. Линейная свертка
- •10.2.1.5. Максиминная свертка
- •10.2.1.7. Целевое программирование (цп)
- •19. Интерактивные методы принятия решений
Транспортная задача с ограниченными пропускными способностями (Td - задача)
Учет ограничений на пропускные возможности коммуникаций. В реальных условиях пропускные способности дорог, воздушных коридоров, линий связи и т.п. всегда ограничены сверху. Учет этих ограничений приводит Тd-задаче. Ее модель имеет вид
|
(7) |
|
(8) |
|
(9) |
0 Xij dij, i,j, |
(10) |
где
dij
–пропускная способность коммуникации
i
j.
В Тd-задаче
условие сбалансированности не является
достаточным для разрешимости задачи.
Более того, в число необходимых условий
существования решения помимо его входят
еще две группы условий, отражающих
физическую реализуемость решения: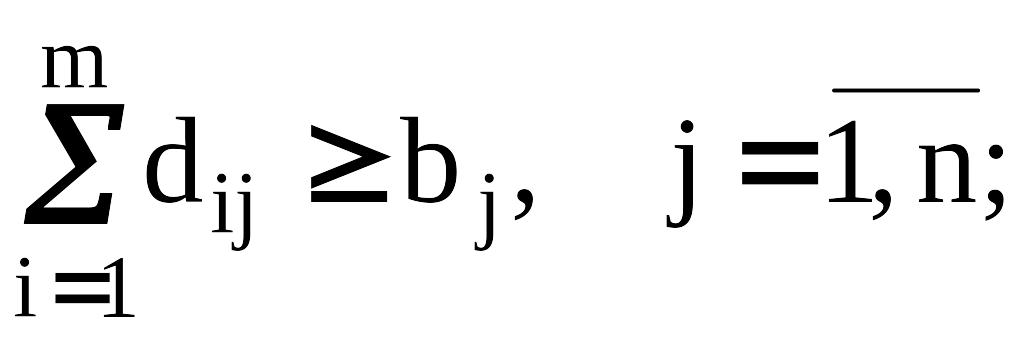 (11)
(11)
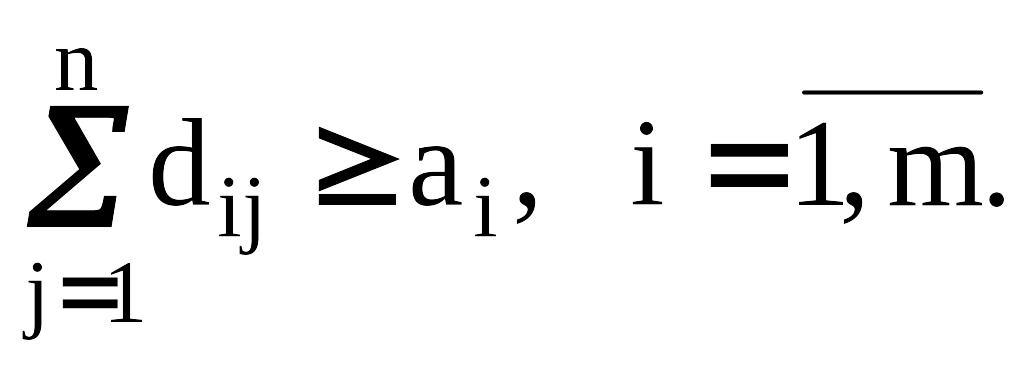 (12)
Они требуют, чтобы суммарная пропускная
способность коммуникаций, входящих в
каждый ПН была не меньше объема поставок,
а выходящих из ПО – не меньше количества
вывозимого груза. Если хотя бы одно из
них нарушается, задача заведомо
неразрешима. Но и выполнение всех
необходимых условий не гарантирует
разрешимость Тd-задачи.
(12)
Они требуют, чтобы суммарная пропускная
способность коммуникаций, входящих в
каждый ПН была не меньше объема поставок,
а выходящих из ПО – не меньше количества
вывозимого груза. Если хотя бы одно из
них нарушается, задача заведомо
неразрешима. Но и выполнение всех
необходимых условий не гарантирует
разрешимость Тd-задачи.
Задачи с неоднородным грузом
В
рассмотренных задачах по умолчанию
предполагалось, что для отправителей
и получателей грузы неразличимы – это
задачи с однородным грузом. Если в
перевозках участвуют несколько видов
груза с одинаковыми или различными
транспортными затратами, исходную
многопродуктовую задачу можно разбить
на задачи с однородным грузом (по числу
видов). Если же имеет место взаимозаменяемость
грузов у получателей, то исходную задачу
нельзя разделить на отдельные задачи.
Такие задачи называют задачами с
неоднородным
грузом.
В случае отсутствия ограничений на
пропускные способности они легко
преобразуются к задачам с однородным
грузом. Взаимозаменяемость грузов
характеризуется коэффициентом
взаимозаменяемости
![]() .Зная
.Зная
![]() все грузы можно привести к одному виду.
Затем вместо одного исходного ПО вводится
столько, сколько в нем видов груза.
Аналогично каждый исходный ПН заменяется
новыми, число которых равно числу видов
потребностей. Наконец, определяются
приведенные затраты на перевозки между
всеми новыми пунктами. Если виды грузов
в ПО и ПН совпадают, затраты на перевозку
равны исходным Cij;
если же они разные, то перевозка
запрещается (Cij=М).
Между ПО с пересчитанным грузом
все грузы можно привести к одному виду.
Затем вместо одного исходного ПО вводится
столько, сколько в нем видов груза.
Аналогично каждый исходный ПН заменяется
новыми, число которых равно числу видов
потребностей. Наконец, определяются
приведенные затраты на перевозки между
всеми новыми пунктами. Если виды грузов
в ПО и ПН совпадают, затраты на перевозку
равны исходным Cij;
если же они разные, то перевозка
запрещается (Cij=М).
Между ПО с пересчитанным грузом
![]() и
ПН с взаимозаменяемой потребностью
затраты равны
и
ПН с взаимозаменяемой потребностью
затраты равны
![]() После таких преобразований модель
задачи записывается аналогично случаю
с однородным грузом, а ее размерность
определяется числом пунктов, заменяющих
исходные. Для разрешимости задачи
необходимо
кроме
сбалансированности, чтобы по каждому
виду груза суммарные возможности были
не меньше суммарной потребности (без
учета взаимозаменяемой). Однако и при
выполнении всех необходимых условий
возможна неразрешимость задачи из-за
присутствия запрещенных перевозок.
После таких преобразований модель
задачи записывается аналогично случаю
с однородным грузом, а ее размерность
определяется числом пунктов, заменяющих
исходные. Для разрешимости задачи
необходимо
кроме
сбалансированности, чтобы по каждому
виду груза суммарные возможности были
не меньше суммарной потребности (без
учета взаимозаменяемой). Однако и при
выполнении всех необходимых условий
возможна неразрешимость задачи из-за
присутствия запрещенных перевозок.
Многоиндексные задачи
Для учета дополнительных условий перевозки вводятся переменные с числом индексов более двух. В таких случаях говорят о многоиндексных транспортных задачах. Например, если существенное значение имеет вид транспорта, то в модели используются переменные Xijk, означающие количество груза, перевозимое из i-го пункта в j-й k-ым видом транспорта. Модель трехиндексной задачи зависит от конкретных условий. Если в исходных данных имеем производительность каждого вида транспорта pk и не учитываются пропускные способности, то задача описывается трипланарной моделью:
|
|
|
|
Она
идентична Т-задаче. Отличие лишь в числе
переменных и групп условий. Поэтому
каждая переменная входит в модель ровно
три раза, а сбалансированность, как
необходимое и достаточное условие
разрешимости задачи, записывается в
виде
![]() Дальнейшая детализация условий
транспортировки может потребовать
переменных с пятью и более индексами.
В ряде случаев многоиндексные задачи
удается свести к двухиндексным.
Дальнейшая детализация условий
транспортировки может потребовать
переменных с пятью и более индексами.
В ряде случаев многоиндексные задачи
удается свести к двухиндексным.