4.2.3. Сбалансированная транспортная задача

Транспортная задача - это модель ситуации, в которой требуется найти оптимальный план перевозки некоторого груза из конечного числа пунктов поставки (отправления) с заданными объемами производства в конечное число пунктов потребления (назначения) с требуемыми объемами потребностей при известных затратах на перевозку единицы груза между каждой парой пунктов поставки и потребления. Предполагается, что удельные затраты не зависят от количества перевозимого груза. Здесь под оптимальным понимается план, минимизирующий суммарные затраты на перевозки.

В качестве примера рассмотрим задачу с двумя пунктами отправления и тремя пунктами назначения, схема которой показана на рис.4.1. Здесь а₁ и а₂ – количество груза, которым располагают пункты отправления, b₁, b₂, b₃ – потребности в грузе пунктов назначения.

Задача является сбалансированной, если суммарная потребность равна суммарной возможности. В нашем примере это значит, что

Рис. 4.1.

Если ввести обозначения:

x_ij - количество груза, перевозимого из i-го пункта отправления в j-й пункт назначения;

С_ij – затраты на перевозку единицы груза из i-го пункта отправления в j-й пункт назначения,

то исходные данные вместе с переменными можно представить в одной таблице (табл. 4.3):

Таблица 4.3

Пункты	B1	B2	B3	Количество груза
A1	С11 Х11	С12 Х12	С13 Х13	a1
A2	С21 Х21	С22 Х22	С23 Х23	a2
Потребность в грузе	b1	b2	b3

Так как необходимо минимизировать суммарные затраты по перевозке, то целевая функция запишется в виде

L=C₁₁x₁₁ + C₁₂x₁₂ + C₂₃x₂₃→min.

Каждый пункт назначения должен получить требуемое количество груза. Отсюда следуют равенства, соответствующие этим пунктам

B₁: x₁₁+x₂₁=b₁;

B₂: x₁₂+x₂₂=b₂;

B₃: x₁₃+x₂₃=b₃.

Поскольку задача сбалансированная, весь груз из пунктов отправления должен быть вывезен. Это требование отражается в модели двумя равенствами:

А₁: х₁₁+х₁₂+х₁₃=а₁;

А₂: х₂₁+х₂₂+х₂₃=а₂.

Наконец, физический смысл переменных накладывает на них ограничение неотрицательности

x_ij0.

В результате мы получили модель транспортной задачи, содержащей только линейные функции. Очевидно, что характер модели не изменится при увеличении числа пунктов.

13. Классы задач нелинейного программирования и методы их решения. Х арактеристика задач

Методы НП применяются для решения задач с нелинейными функциями переменных.

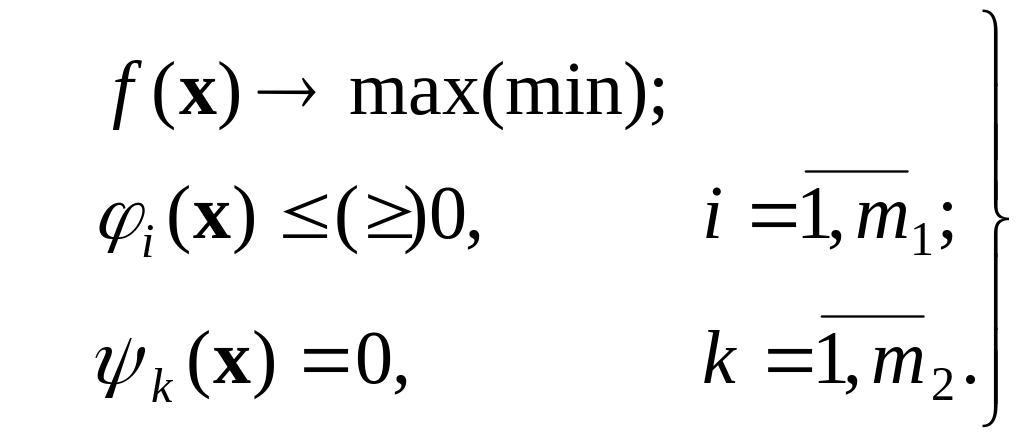(1)

Если хотя бы одна функция в модели (1) нелинейна, имеем задачу нелинейного программирования (НП). Cложность задачи определяется свойствами функций цели и ограничений.

Универсальных методов решения таких задач не существует.

Наиболее развиты методы решения задач выпуклого программирования.

1. Допустимое множество выпукло.

2. Свойство целевой функции: min – выпуклая, max – вогнутая.

Допустимое множество выпуклое, если все функции линейные и выпуклы при неравенстве  или вогнуты при .

Главная особенность задач выпуклого программирования в том, что они унимодальны, то есть любой их локальный оптимум является глобальным. Для ряда задач выпуклого программирования с дифференцируемыми функциями разработаны точные методы.

- Задачи квадратичного программирования. В них целевая функция представляет собой сумму линейной и квадратичной форм, а все условия линейные.

- Задачи сепарабельного программирования. Все функции сепарабельны. Функция сепарабельна, если она представляется в виде суммы функций отдельных переменных.

- Задачи геометрического программирования. Все функции являются позиномами. Позиномом называется функция , в которой _kj – любые действительные числа. Задачи геометрического программирования ставятся только на минимум:

- Кусочно-линейное программирование. Путем преобразования сводятся к линейным и решаются соответствующими методами. В частности, такими являются функции

и

К линейным сводятся также задачи дробно-линейного программирования. Они отличаются от линейных только дробной целевой функцией, числитель и знаменатель которой – линейные функции.