Двойственный симплекс-метод

Прямая задача решается двойственно: в начальном и последующих базисных решениях выполняются условия оптимальности (все оценки неотрицательны при максимизации), но вектор Х неположителен, а значит, недопустим. В разрешимой задаче итерации метода приводят к допустимому Х, который и будет оптимальным решением задачи.

Поэтому цикл начинается с анализа базисных переменных. Если все переменные неотрицательны, вычисления завершаются. Иначе выбирается направляющая строка k по минимальной базисной переменной. Затем вычисляются значения 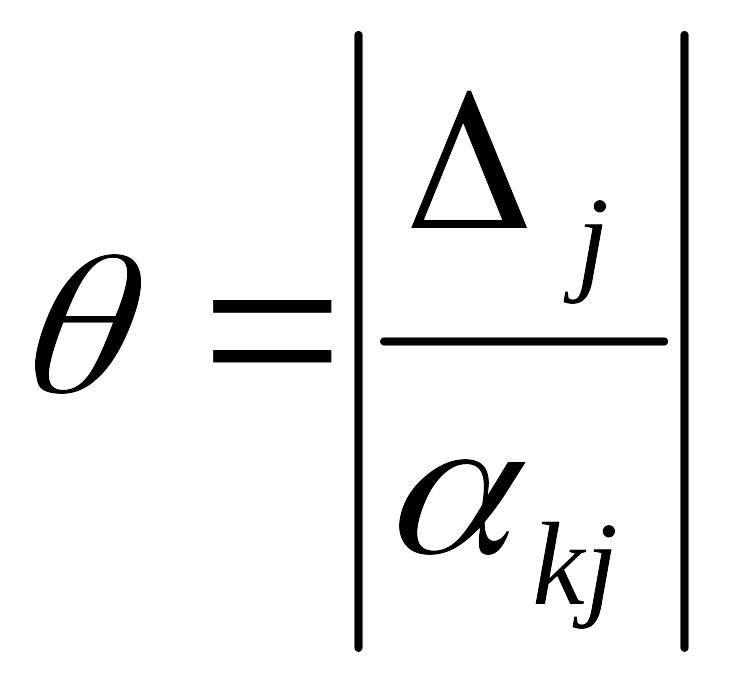: для < 0.(40)

Если в прямом методе формула следует из требования получения нового неотрицательного решения, то здесь – из необходимости соблюсти в новом решении условия оптимальности. При отсутствии в направляющей строке отрицательных kj констатируется неразрешимость задачи из-за противоречивости условий. Действительно, равенство с отрицательной правой частью и всеми неотрицательными коэффициентами при переменных в левой части не может быть удовлетворено неотрицателными переменными. Направляющий столбец r определяется по минимальному . Далее текущая симплекс-таблица пересчитывается так же, как в прямом методе. В результате получается новое базисное решение, в котором, по крайней мере, xk станет неотрицательной.

В разрешимой задаче такой алгоритм приведет к оптимальному решению за конечное число итераций. Двойственный метод отличается от прямого свойствами начального решения и правилами выбора направляющего элемента.

9. Декомпозиция задач планирования большой размерности.

При решении задач большой размерности значительная часть времени тратится на обращения к внешней памяти и это является главным препятствием на пути увеличения размерности задач. Уменьшить число обращений к внешней памяти можно, если удается большую задачу заменить рядом задач существенно меньшей размерности. Приемы и методы, позволяющие выполнять такие преобразования, составляют предмет блочного программирования.

Метод декомпозиции Данцига - Вулфа

Рассмотрим математические преобразования, приводящие к разбиению исходной задачи, а затем покажем, в каких случаях это дает эффект по сравнению с непосредственным решением большой задачи. Пусть имеется следующая модель задачи:

L=C^TXmax;(1) AX=B;(2) X0, (3) где вектор X имеет размерность n, а вектор B – m. Условия (2), (3) определяют допустимое множество задачи D. Представим матрицу А и вектор В в виде двух подматриц: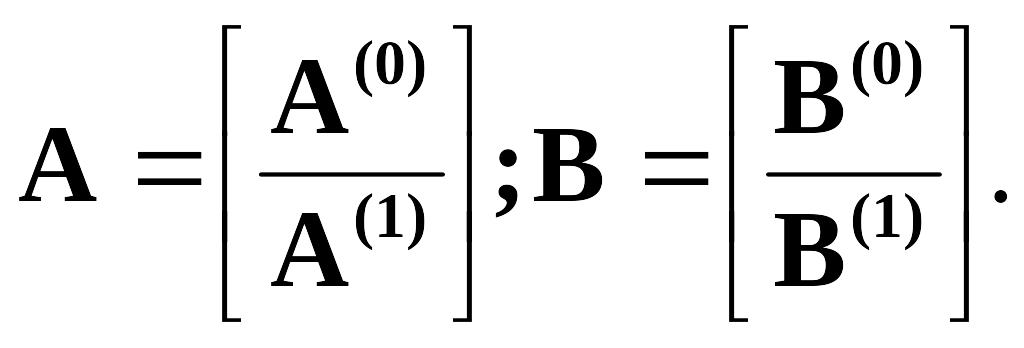 Тогда условия задачи (2)-(3) записываются следующим образом:

А⁽⁰⁾Х=В⁽⁰⁾;(4) А⁽¹⁾Х=В⁽¹⁾;(5) Х0(6)

Условия (4), включающие m₀ равенств, порождают допустимое множество D₀, а система (5) содержит m₁ равенств и вместе с (6) задает множество D₁. Очевидно, что m=m₀+m₁, D= D₀  D₁. При этом выделение подматриц выполняется так, что m₁>>m₀.

Далее будем полагать, что множество D₁ ограниченное и, значит, является выпуклым многогранником. В противном случае его легко сделать ограниченным добавлением ограничений сверху на переменные так, что они не повлияют на исходное множество D.

Предположим, что нам известны вершины множества D₁. Обозначим их координаты через Х¹, Х²,…, Х^N, где N – число вершин. Поскольку D₁ – выпуклый многогранник, то любую его точку можно представить в виде линейной комбинации вершин:

Х= z_X^;(7)  z_=1;(8) z_0, v.(9)

Так как все решения Х, определяемые по (7)-(9), принадлежат D₁, то описание (7)-(9) эквивалентно (5), (6). Подставим Х в виде (7) в (1) и (4): L = C^T z_X^;

A⁽⁰⁾X^z_=B⁽⁰⁾. Считая X^ известными, введем обозначения: С^ТХ^=_; (10)

А⁽⁰⁾Х^=Р_.(11) Тогда преобразованная модель задачи запишется в виде

L= _z_max; P_z_=B⁽⁰⁾; z_=1; z_0.

В этой модели неизвестными являются z_, число которых равно числу вершин многогранника D₁. Последнее равенство модели можно объединить со всеми остальными, используя обозначения расширенных векторов 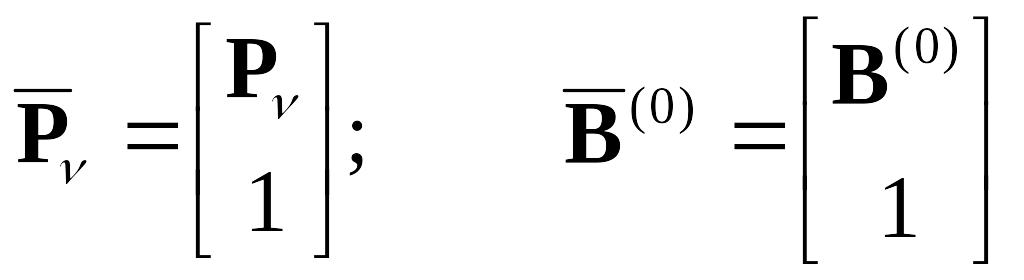.(12)

Тогда окончательно получим:L= _z_max;(13) z_ = ; (14)z_0. (15)

Задача в виде (13) – (15) называется координирующей или основной задачей. Главное отличие этой задачи от исходной в несравнимо меньшем числе условий (m₀+1<<m). Если мы сможем ее решить, то есть найти Z^*, то получим решение и исходной задачи, воспользовавшись (7): Х*= z_^*X^.(16)

Для решения основной задачи применим модифицированный симплекс-метод. Начальное решение можно построить, не зная ни одной вершины, с помощью искусственных переменных z_N+i. Согласно модифицированному методу после получения очередного базисного решения вычисляются относительные оценки.

Перепишем их в обозначениях координирующей задачи: (17)

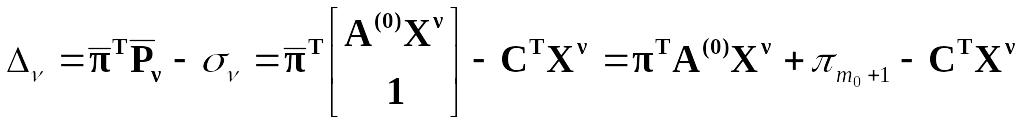или окончательно

(18)

Мы не можем вычислить все оценки, так как нам не известно даже их число. Но этого и не требуется, достаточно только определить: есть или нет среди них отрицательные. Будем искать наименьшую оценку. Если она отрицательная, текущее решение координирующей задачи может быть улучшено введением переменной с этой оценкой. В противном случае констатируется выполнение признака оптимальности.

Задача состоит в следующем: _min.

Отбросив в (18) константу, запишем ее в виде (^TA⁽⁰⁾-C^T)X^ (19)

Решение задачи (19) проблематично, так как минимум ищется на дискретном множестве вершин многогранника D₁. Учитывая, что минимизируемая функция линейная, будем искать решение не на вершинах, а на всем многограннике. Известно, что если решение существует, то оно будет достигаться в вершине. Поэтому решение на всем (непрерывном) множестве D₁ совпадет с решением задачи (19). Задачу (19) заменяем эквивалентной: L_всп= (^TA⁽⁰⁾-C^T)X (20) A⁽¹⁾X = B⁽¹⁾; (21) X  0. (22)

Эта задача называется вспомогательной. Если она неразрешима, то и исходная задача не имеет решения. Пусть оптимальное решение вспомогательной задачи (20)-(22) достигается в вершине r. Это означает, что нам становятся известны координаты вершины X^r и оптимальное значение критерия . То согласно формуле (18) вычисляем минимальную оценку (23)

Если _r0, то и все оценки неотрицательны, и решение координирующей задачи завершено. При отрицательной _r решение продолжается. В базис основной задачи вводится вектор , определяемый по формуле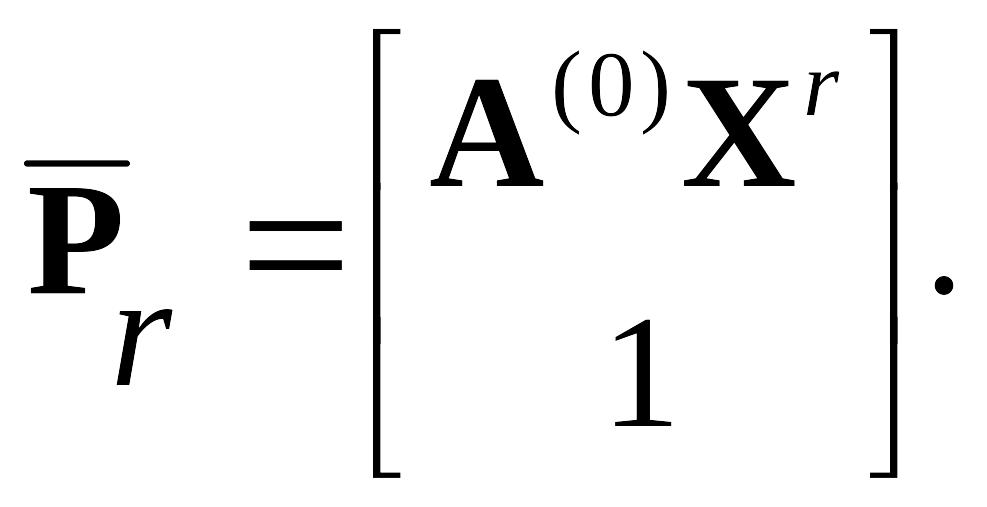 (30) Направляющий столбец находится разложением этого вектора по текущему базису: . (31)

После определения направляющего элемента и симплекс-преобразования получаем новое решение основной задачи. Коэффициент критерия (13) при переменной, введенной в базисное решение, вычисляется согласно (10):_r =C^TX^r. (32)

По формуле (17) находим новый вектор , снова решаем вспомогательную задачу и по полученной минимальной оценке делаем вывод о дальнейших действиях.

Решение исходной задачи заменяется многократным решением основной и вспомогательной задач. При этом порядок размерности вспомогательной задачи такой же, как у исходной. В тех случаях, когда сложность решения вспомогательной задачи намного ниже, чем исходной. Такие случаи имеют место, когда матрица условий задачи (после упорядочения строк и столбцов) оказывается почти-блочно-диагональной. Примером может служить задача планирования производства продукции в крупной фирме или холдинге, когда у каждого предприятия своя номенклатура продукции, а некоторые ресурсы являются общими. Подматрица А⁽⁰⁾, входящая в параметры координирующей задачи, соответствует ограничениям по общим ресурсам. Такие условия называют связующими. Их относят к основной задаче.

О стальные условия образуют вспомогательную задачу. При этом подматрица А⁽¹⁾ имеет блочно-диагональную структуру, что позволяет разбить вспомогательную задачу на p независимых задач:

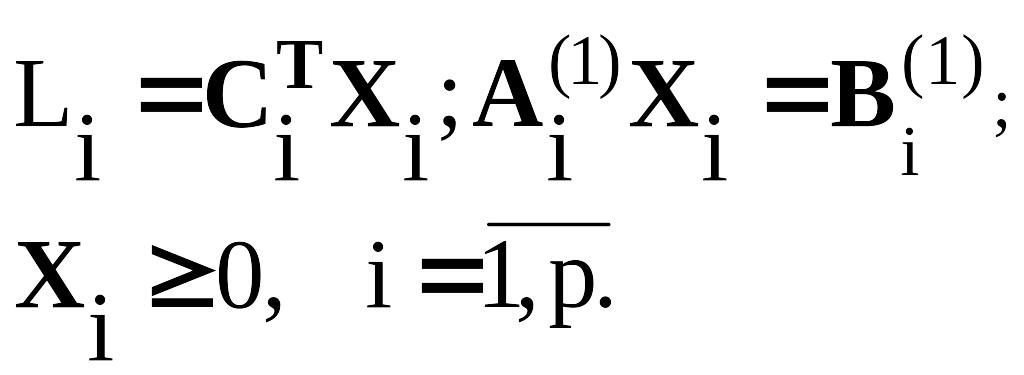
После решения этих задач определяется критерий вспомогательной задачи по очевидной формуле Решение вспомогательной задачи существенно упрощается, если структура матрица условий может быть приведена к блочно-диагональной.

Решение транспортной задачи методом Данцига-Вулфа

Применим метод декомпозиции к Т-задаче: (33)

(34) (35) Х_ij0. (36)

Использование этого метода целесообразно, если m<<n или m>>n. Оба варианта решаются идентично. Они отличаются только распределением условий между основной и вспомогательной задачами. Рассмотрим случай, когда m<<n. Тогда основная задача формируется по условиям пунктов отправления. Следовательно, множество D₀ описывается ограничениями (34), а D₁ – условиями (35) и (36). Множество D₁ представляет собой выпуклый многогранник (ограниченность вытекает из условий). Поэтому любую точку в D₁ можно представить в виде линейной комбинации его вершин: (37) Z_v=1; (38) Z_v0, (39)

где X^v_ij – координаты v-ой вершины. Подставим (37) в (33) и (34):

. Введем обозначения: (40) (41)

Тогда основная задача запишется в виде (42)

(43) (44) Z_v 0. (45)

Суммируя (43) и используя подстановки (41) и (35), получаем в левой части

в правой части Получаем откуда для сбалансированной задачи следует Поэтому при решении основной задачи условие (44) из модели исключается.

Для определения статуса текущего базисного решения основной задачи необходимы относительные оценки. Для построения вспомогательной задачи сделаем ряд преобразований:_v= ^TP_v - _v =

Так как основная задача решается на минимум, то оптимальному статусу соответствуют неположительные оценки. Поэтому нужно искать максимальную оценку. Если она окажется не больше нуля, то все оценки неположительны и признак оптимальности выполнился. В противном случае необходимо продолжить решение основной задачи.

Задача ставится так:

Вместо поиска максимума на дискретном множестве вершин перейдем к эквивалентной задаче поиска на всем непрерывном множестве D₁:

(46) (47) X_ij  0.(48)

Эта задача является вспомогательной. В оптимальном решении этой задачи

Вспомогательная задача включает одну группу условий (47). Каждая переменная входит в такие условия только один раз. Поэтому равенства (47) оказываются независимыми и вспомогательная задача распадается на n простейших независимых задач, каждая из которых имеет всего одно условие: (49)

(50) X_ij  0.(51)

Критерий вспомогательной задачи равен сумме критериев этих задач: (52)

Оптимальное решение задачи (49)-(51), как линейной, находится на границе. При этом только одна переменная не равна нулю (базис имеет размерность 1). Поэтому ее решение состоит в определении максимального коэффициета в критерии (49). Пусть максимум достигается на индексе i*, то есть

Тогда имеем следующее решение задачи (49)-(51): X^v_i*j =b_j, X^v_ij=0, i, ii*, (53)

и максимальная оценка определится как .

Если L^*_всп  0, то положительных оценок нет и текущее решение основной задачи будет оптимальным.

При L^*_всп > 0 начинается новая итерация:

1. пo (41) и (40) находим Р_v и _v;

2. вычисляем элементы направляющего столбца как коэффициенты разложения вектора Р_v по текущему базису: _v=P^-1_BP_v;

3. проводим симплекс-преобразование основной задачи, в результате которого получаем новое решение и новую обратную матрицу;

4. вычисляем ^T=^T_BP^-1_B;

5. решаем вспомогательную задачу: вычисляем разности , находим оптимальные решения n задач (49)-(51) и максимальную оценку основной задачи.

Из рассмотренной вычислительной схемы следует, что эффективность метода тем выше, чем сильнее неравенство m<<n или m>>n.