300.Двумерные цф

Сущ. задачи, где данные предст. собой двумерный массив чисел. Это задачи, связ. с обраб. изображений — TV, косм. исслед-ия, картография и т.д. — задачи ↑ контрастности, выделения контуров, плохо различимых деталей и т.д.

Данные в них имеют статистическую зависимость как во времени, так и в простр-ве. Одномерные сигналы имеют статистическую связь лишь по оси времени.

Т.к. статистическая связь в одномерных сигналах ↓ с увеличением сдвига во времени, то совместно обраб-ся лишь группа соседних отсчетов сигнала.

Двумерные сигналы обраб. с пом. спец. устр-в, кот. преобр. двумерную группу соседних отсчетов сигнала или матрицу вх. сигнала в гр. или матр. вых. сигнала.

Обработка всего изображения достигается при перемещении матриц по плоскости изображения.

301.Перечислите формы аппроксимации типовых ачх цф

Когда преобразование спектра заключается лишь в подавлении и/или усилении участка спектра сигнала, преобразование выполняется с помощью линейного фильтра. Рассматривают 4 вида фильтров:

ФНЧ, ФВЧ, полосовой, режекторный.

Способы аппроксимации:

Ф Баттерворта: max гладкая АЧХ и в полосе задержания и в полосе пропускания

Ф Чебышева1: гладкая АЧХ в полосе задержания, пульсирующая в полосе пропускания.

Ф Чебышева2: гладкая АЧХ в полосе пропускания, пульсирующая в полосе задержания.

Эллиптический Ф. пульсирующая АЧХ в обеих полосах

302.Теорема Котельникова

Теоре́ма Коте́льникова гласит, что, если непрерывный сигнал имеет ограниченный частотой Fгр спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчётам, взятым через интервал времени T=1/2Fгр

При слишком редкой дискретизации и происходит наложение сигналов из разных периодов друг на друга .При этом форма периодической последовательности будет отличаться от формы одиночного сигналавсе наложения (сигналов или спектров) происходят из-за неудачного – слишком редкого – интервала дискретизации (соответственно, спектра или сигнала). Это приводит к появлению ошибок наложения, или, другими словами, искажений формы сигнала (либо спектра) на каждом периоде. .(пример на рисунке)

303.Проанализируйте выбор частоты дискретизации для сигналов с ограниченным и протяженным спектром

Интервал времени T, через который отсчитываются значения непрерывного сигнала i(t) называется интервалом дискретизации. Обратная величина 1/T (обозначим ее Fд) называется частотой взятия отсчетов или частотой дискретизации. Отсчеты непрерывного сигнала следует брать с такой частотой (или через такой интервал времени), чтобы успевать отследить все, даже самые быстрые, изменения сигнала. Иначе, при восстановлении этого сигнала по дискретным отсчетам часть информации будет потеряна и форма восстановленного сигнала будет отличаться от формы исходного (пример на рисунке). Если обратиться к схеме рис. 1, то это означает, что звук на приеме будет восприниматься с искажениями.

304.Опишите причины наложения спектров

Выбор периода дискретизации основывается на одном из следующих критериев:

1. По т. Котельникова если период дискр. удовл. условию Т< 1/(2F_max), где F_max - max частота в спектре сигнала x(t), то потерь инф-ии в рез-тате дискретизации не происходит, т.к. непрер. сигнал x(t) полностью восстанавливается по своим отсчетам.

2. По т. Железнякова если спектр сигнала не ограничен, то период дискретизации м.б. выбран из условия Т <_корр где

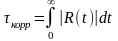
_корр - время корреляции сигнала x(t), определяющее статистич. связь между двумя отсчетами сигнала:

R(t)=B(t)/B(0)

B(t)–корр. ф-ия сигнала x(t); В(0)–ср. мощ. сигнала x(t)

В рез-тате дискретиз. врем.сигнала f(t), его спектр периодически повторяется с частотой =2/T, F_g=1/T.

При неверном выборе F_д появляется эффект наложе-ния спектров, приводящий к искажению врем сигнала.

Обратимся вновь к рис. 9. В случае, когда дискретизации подвергается спектр (рис. 9, б), это приводит к периодическому повторению сигнала. На рис. 9, б и 13, а, б показаны случаи выбора разных интервалов дискретизации спектров. При слишком редкой дискретизации и происходит наложение сигналов из разных периодов друг на друга (рис. 13,б). При этом форма периодической последовательности будет отличаться от формы одиночного сигнала.

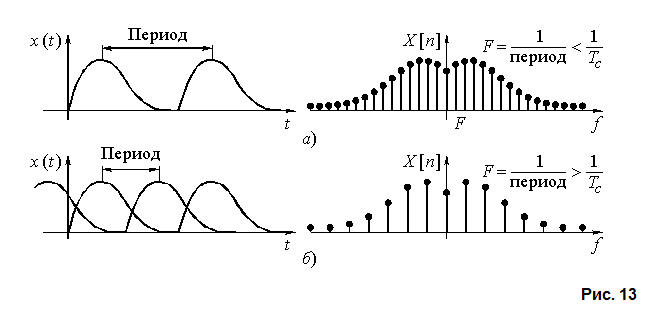
Если дискретизации подвергается сигнал (рис. 14, а, б и 15 а, б), то периодически повторяется спектр сигнала. При неудачном выборе интервала дискретизации будет иметь место наложение друг на друга спектров из разных периодов повторения, т.е. искажение формы спектра (рис. 14, б и 15, б).

Вывод: все наложения (сигналов или спектров) происходят из-за неудачного – слишком редкого – интервала дискретизации (соответственно, спектра или сигнала). Это приводит к появлению ошибок наложения, или, другими словами, искажений формы сигнала (либо спектра) на каждом периоде