Рассмотрим методику графического решения злп с помощью winqsb.

Решим пример 2.1.

Для решения надо выполнить следующие действия.

1. Включить компьютер.

2. Найти и открыть папку WINQSB.		3. Загружаем файл LP-I LP (Линейное программирование)	4. Активизируем курсором файл

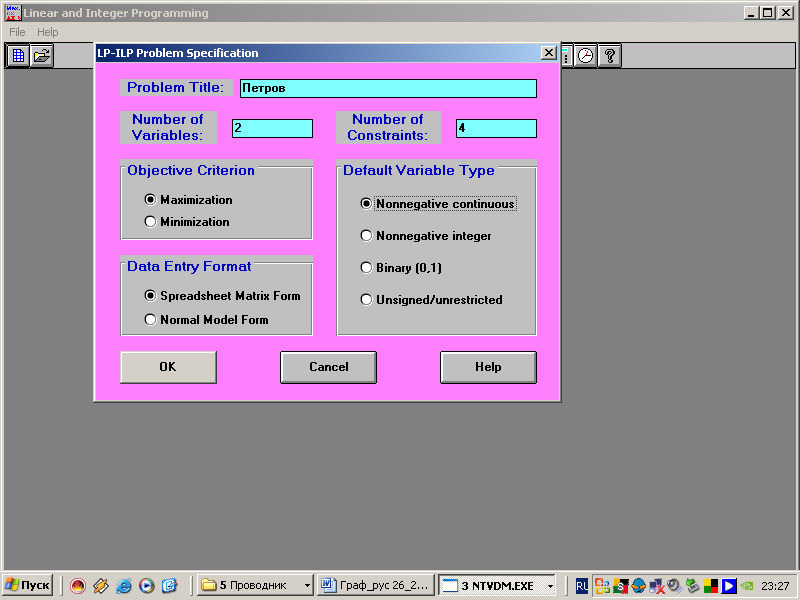
5. В появившуюся таблицу вносим данные:

• Имя проблемы, например Петров;

• Количество переменных, в нашем примере 2;

• Количество ограничений, в нашем примере 4;

• Курсором устанавливаем Maximization, так как наша задача на max;

• OK.

6. В появившуюся таблицу вводим числовые коэффициенты задачи.

Таблица 2.2

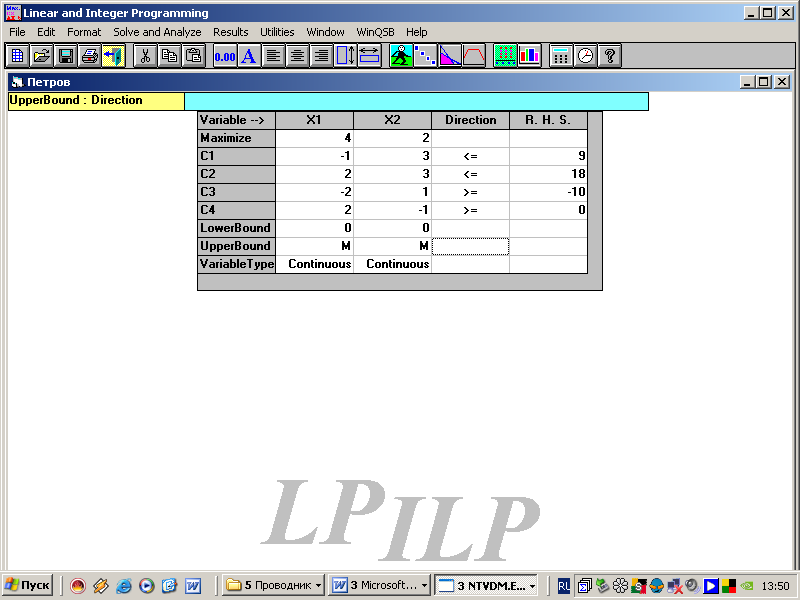
Для изменения знака <= на = или >= необходимо последовательно активизировать мышкой клетку, в которой находится соответствующий знак.

Числа 0, М в строках Lower Bound, Upper Bound указывают диапазон изменения переменных . Если в столбце вместо 0 поставить 4, а вместо М 12, то это будет означать, что может принимать значения с отрезка .

7. Выполнить действие, графическое решение: .

8. В появившемся окне выполняем действие ОК.

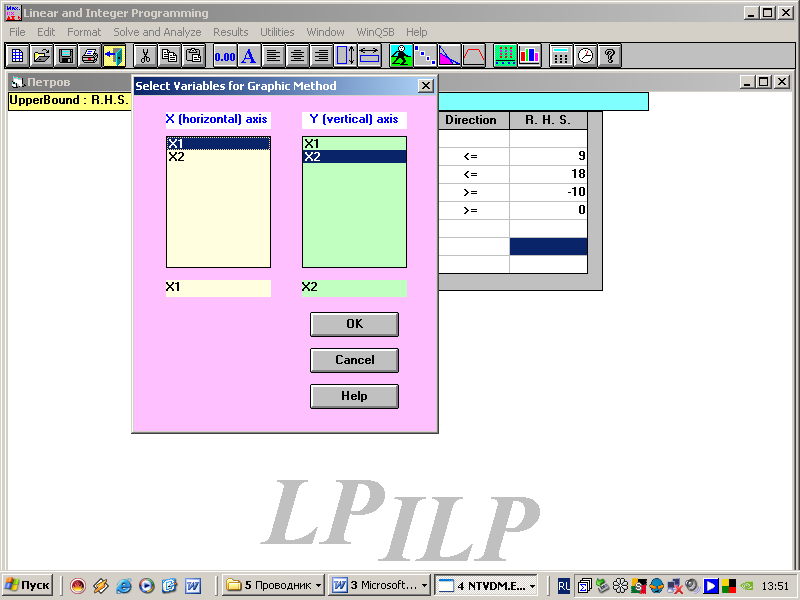
9. Получили графическое решение задачи.

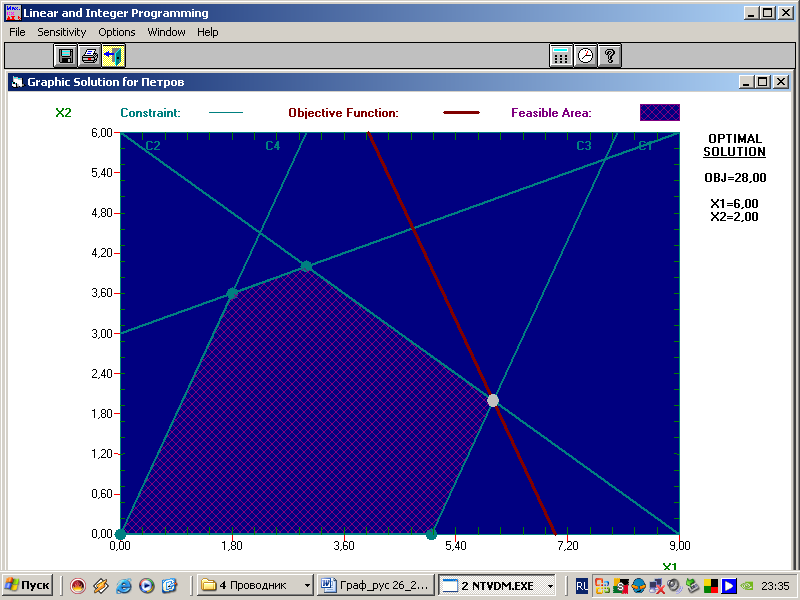
Рис. 2.3

Рисунок полностью соответствует рисунку в примере 2.1.

На рисунке написано оптимальное значение целевой функции OBJ=28.00 и значения переменных х₁=6.00, х₂=2.00, при которых принимается оптимальное значение.

Этот рисунок можно напечатать.

Аналогично эту задачу можно решать с помощью программы QSB (см. стр. 33).

Для того чтобы копировать рисунки, таблицы или весь экран для их вставки в выбранные файлы можно поступить следующим образом.

1. Нажатием клавиши Prt Scr копируем весь экран монитора.

2. В требуемом файле с помощью Правка + Вставить получаем вид всего экрана.

3. Обрезанием оставляем то, что нужно. Для этого курсором активизируем рисунок и знак . Перетягиваем значок в один из углов рисунка монитора. Нажимаем левую клавишу мышки, чтобы появился знак . Перемещая его, делаем обрезание рисунка.

3. Симплексный метод решения задач линейного программирования

Пример 3.1. Для выпуска двух видов продукции по цене 2 грн. и 3 грн. используется три вида сырья с запасами 60 кг, 54 кг, 60 кг. Расходы сырья на единицу продукции первого вида соответственно равны 3; 1; 2 кг, второго — 2; 3; 3 кг. Данные сведены в таблицу.

Таблица 3.1

Сырьё	Продукция (расходы сырья на единицу продукции)		Запасы сырья
	P1	P2
S1	3 кг	2 кг	60 кг
S2	1 кг	3 кг	54 кг
S3	2 кг	3 кг	60 кг
Цена един. продукции	2 грн.	3 грн.
Количество продукции	x1	x2

Найти план выпуска продукции, чтобы доход от её реализации был максимальный.

Решение. Обозначим через х₁ количество выпуска продукции первого вида, х₂ – второго вида, Z – доход от реализации всей продукции. Тогда математическая модель задачи принимает вид:

(3.1)

Переходим к каноническому виду. Для этого добавляем или вычитаем в каждом ограничении дополнительную (балансовую) неотрицательную переменную, если оно не равенство, чтобы преобразовать его в равенство. Равенство оставляем без изменения. Если задача на min, то целевую функцию оставляем без изменения, если на max, то делаем замену .

(3.2)

Систему ограничений удобно записывать в векторной форме

, (3.3)

где

(3.4)

Представление является разложением вектора по векторам За базис этой системы векторов можно взять систему единичных векторов . Базисное решение будет определять начальный опорный план.

Выпишем начальный опорный план и значение целевой функции для него. Для этого свободные переменные приравниваем к нулю: а базисные переменные после этого находятся из системы:

.

Для решения задачи составляем симплексную таблицу.

Симплексная таблица составляется следующим образом. В первой строке шапки симплекс – таблицы указаны векторы исходной системы ограничений задачи, а во второй – коэффициенты при переменных в целевой функции задачи. В первом столбце (столбец ) указаны векторы, образующие базис заданной системы векторов, а во втором столбце –коэффициенты целевой функции при базисных переменных. Во всех остальных клетках таблицы (кроме последней строки, о которой будет сказано ниже) стоят коэффициенты разложения соответствующих векторов по векторам базиса.

Так как для нашей задачи выбран единичный базис, то в первой симплексной таблице в столбцах будут стоять соответствующие коэффициенты системы ограничений.

Последняя строка называется индексной или -ой. В третьем столбце этой строки стоит значение целевой функции при проверяемом оптимальном плане , а во всех остальных клетках индексной строки стоят оценки оптимальности для векторов исходной системы. Здесь – значение целевой функции, если в неё вместо переменных подставить коэффициенты разложения вектора , а – коэффициенты целевой функции при соответствующих переменных.

Таблица 3.2

									
																2
						-2		-3		0		0		0
			0	60		3		2		1		0		0		60/2=30
			0	54		1		[3]		0		1		0		54/3=18			-2/3	-1
			0	60		2		3		0		0		1		60/3=20
				0		2		3		0		0		0

Индексная строка рассчитывается следующим образом.

(3.5)

. (3.6)

В первой симплексной таблице имеем:

= 060+054+060 = 0, z₁-c₁ = 03+01+02– (–2) =2,

z₂-c₂ = 02+03+03– (–3) = 3, z₃-c₃ = 01+00+00–0 = 0,

z₄-c₄ = 00+01+00-0 = 0, z₅-c₅ = 00+00+0- 0 = 0.

В общем случае

(3.7)

При анализе решений удобно говорить о переменных. Поэтому в таблицах вместо векторов можно указывать переменные . Балансовые и искусственные переменные иногда обозначают другими буквами.

Число 3 в индексной строке показывает, что если вторую переменную увеличить на единицу, то целевая функция уменьшится на 3. Исходя из этого, легко понять методику решения симплексным методом ЗЛП. Поэтому опорный план будет оптимальным, если все оценки .

На единицу второй продукции используется 2 кг первого сырья, запас которого 60 кг. Поэтому запас первого сырья допускает выпуск второй продукции не более чем 60/2=30 единиц. Запас второго сырья дает ограничение . Запас третьего сырья дает ограничение . Поэтому х₂ можно увеличивать максимально от нуля до 18. Если бы а_i2=0, то i-ое сырье для изготовления второй продукции не использовалось бы и запас i-го сырья не влиял бы на изменение х₂. Если а_i2<0, то это можно интерпретировать как возникновение а_i2 кг i-го сырья при изготовлении единицы продукции второго вида. Поэтому и в этом случае запас i-го сырья не влиял бы на увеличение величины х₂. Таким образом, предельно допустимое увеличение х₂ определяется соотношением, которое называется симплексным

. (3.8)

В общем виде симплексное отношение находится по формуле

. (3.9)

Симплексное отношение находится лишь для положительных . По симплексному отношению вторую переменную мы можем увеличить на 18. Поэтому при втором опорном плане значения целевой функции будет равняться 0-18·3 = – 54.

Критерий оптимальности решения задач линейного программирования симплекс-методом написан на стр. 26 алгоритма решения.

Из-за того, что в индексной строке есть положительные числа, то план не оптимален. Переходим к новому плану. Направляющий столбец выбираем по наибольшему числу в индексной строке. Это есть второй столбец. Поэтому вектор вводим в базис. Направляющую строку выбираем по минимуму симплексного отношения (вектор выводим из базиса).

Составляем новую симплексную таблицу.

В столбце мы должны получить единичный столбец. Для этого разрешающую строку делим на разрешающий элемент (в нашем случае на 3). К первой строке системы прибавляем разрешающую строку, умноженную на (-2/3). Разрешающую строку умножаем на (–1) и прибавляем к третьей строке. Точно так же пересчитываем индексную строку и соответственно меняем первый и второй столбцы в таблице.

Элементы, которые находятся не в разрешающей строке и столбце, иногда удобно пересчитывать по правилу прямоугольника:

Таблица 3.3

apr	…	apj			…	0
…		…		…		…
air	…	[aij]			…	1

(3.10)

– правило прямоугольника.

Это правило получается следующим образом.

1. Элементы направляющей i-ой строки делим на разрешающий элемент .

2. Для того, чтобы в направляющем столбце все остальные элементы стали равными нулю, элементы полученной строки умножаем последовательно на и прибавляем к соответствующем элементам p-ой строки. Тогда вместо числа в p-ой строке станет число или .

Например,

Для контроля индексную строку можно пересчитывать по формулам правила прямоугольника. Пересчёт элементов в симплексной таблице часто вызывает трудности. Поэтому еще раз обратимся к этому моменту.

Наша задача заключается в том, чтобы столбец для вектора сделать единичным. Чтобы на месте 3 получить единицу, разделим вторую строку системы на 3. Чтобы получить нуль на месте элемента а₁₂ = 2, умножим разрешающую строку на (–2/3) и прибавим к первой строке. Тогда получим

Таблица 3.4

60	3	2	1	0	0	–	Первая строка
-36	-2/3	-2	0	-2/3	0	–	Разрешающая строка, умноженная на -2/3
24	7/3	0	1	-2/3	0	–	Результат векторного сложения