
ЧАСТЬ 1
.pdfЧАСТЬ 1
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА.
ЛАБОРАТОРНАЯ РАБОТА № 1
ИССЛЕДОВАНИЕ УПРУГОГО УДАРА ШАРОВ
Цель работы: закрепление теоретического материала по теме "Законы сохранения в механике".
Задачи работы: вычислить работу деформации и коэффициент восстановления при соударении стальных шаров.
Приборы и принадлежности: Специальная установка для исследования упругого удара шаров.
Краткая теория
Понятие "удар" включает в себя совокупность явлений, возникающих при столкновении движущихся твердых тел, а также при некоторых видах взаимодействия твердого тела с жидкостью или газом (например, удар струи о тело, действие взрывной волны на твердое тело и др.). Промежуток времени, в течение которого длится удар, обычно очень мал ( ~ 10-4 - 10-5с ), а развивающиеся на площадках контакта соударяющихся тел ударные силы очень велики. За время удара они изменяются в широких пределах и достигают значений, при которых средние величины давления (напряжений) на площадках
контакта имеют |
порядок 104-105 атм. Действие ударных сил приводит к |
значительному |
изменению за время удара скоростей точек тела. |
Следствиями удара могут быть остаточные деформации, звуковые колебания, нагревание тел, изменение механических свойств материалов (в частности, их упрочнение), полиморфные и химические превращения и др., а при скоростях соударения, превышающих критические, - разрушение тел в месте удара.
Существуют два предельных вида удара: абсолютно упругий и абсолютно неупругий. Абсолютно упругим называется удар, после которого тела полностью восстанавливают свою первоначальную форму и совершают самостоятельное движение.
Абсолютно неупругим называется удар, после которого деформация тел сохраняется и тела совершают совместное движение.
При абсолютно упругом ударе выполняются закон сохранения импульса и закон сохранения механической энергии. При абсолютно неупругом ударе закон сохранения механической энергии не выполняется, т.к. часть механической энергии идет на образование остаточных деформаций, нагревание тел и др.
Рассмотрим упругое столкновение двух тел. Пусть совершается "центральный удар", при котором центры масс соударяющихся тел движутся по одной прямой,
3
при этом вращательного движения не возникает. В процессе удара возникают кратковременные ударные силы, величина которых много больше всех остальных сил (силы тяжести, сил сопротивления воздуха и т. д.).
Поэтому систему соударяющихся тел можно считать изолированной и записать для нее законы сохранения:
Закон сохранения механической энергии :
|
m V 2 |
|
m V 2 |
|
m u2 |
|
m u2 |
|
|
|
1 1 |
|
2 2 |
|
1 1 |
|
2 2 |
(1) |
|
2 |
2 |
2 |
2 |
||||||
|
|
|
|
||||||
и закон сохранения импульса : |
|
|
|
||||||
|
|
|
m1V1 m2V2 m1u1 m2u2 , (2) |
где m1 и m2 массы тел, |
|||
V1 |
и |
V 2 |
- скорости тел до удара, |
u1 |
и |
u2 |
- скорости тел после удара. |
Решая совместно уравнения (1) и (2), получим формулы для расчета скоростей тел после упругого удара:
u1 |
|
(m1 m2 )V1 2m2V2 |
|
(3) |
|
||
|
m1 m2 |
|
|||||
|
|
|
|
|
|||
u2 |
|
|
(m2 m1 )V2 2m1V1 |
|
(4) |
|
|
|
m1 m2 |
|
|||||
|
|
|
|
|
|||
В них принимается направление скорости V |
за положительное. Скорости u |
, V |
|||||
|
|
1 |
1 |
|
|||
2 , u2 подставляем в формулы с минусом, если их направление противоположно направлению V1.
Формулы (1) - (4) применимы в случае столкновения абсолютно упругих тел. При столкновении реальных тел в формуле (1) следует учесть ту часть механической энергии, которая расходуется на совершение невосстанавливающейся деформации и преобразуется в энергию теплового движения (диссипация энергии) - работу деформации А:
m V 2 |
|
m V 2 |
|
m u 2 |
|
m u 2 |
A |
(5) |
1 1 |
2 2 |
1 1 |
2 2 |
|||||
2 |
|
2 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
4 |
|
По величине "А" оценивают степень " неупругости " удара. По предложению Ньютона степень " неупругости " удара оценивают и по отношению нормальных составляющих скоростей тел после и до удара.
un |
, |
(6) |
Vn
где Vn , un - нормальные составляющие скорости до и после удара.
Это отношение называют коэффициентом восстановления , который зависит от физических свойств материалов тел: ( например: стали =0,55,
стекла = 0,94, cлоновой кости =0,89, дерева =0,50 ).
Метод измерения
В данной работе изучается прямой удар двух шаров из стали, подвешенных на нитях так, что в момент удара они проходят через положение равновесия. При
центральном ударе двух шаров одинаковых |
масс m1 m2 |
m и при условии |
||
равенства скоростей до удара V1 = V2 = V соблюдается равенство скоростей и |
||||
после удара u1 u2 u . Тогда коэффициент восстановления: |
|
|||
|
u |
|
(7) |
|
|
|
|||
V |
|
|
||
найдем из следующих соображений.
Потенциальная энергия шара в момент удара полностью превращается в кинетическую:
mgh mV 2 |
(8) |
||
|
1 |
2 |
|
|
|
|
|
Равенство (8) соблюдается и после удара: |
|
||
mu2 mgh |
(9) |
||
2 |
|
2 |
|
|
|
|
|
5

|
|
|
|
|
Тогда из уравнения (8) и (9) имеем: V 2gh1 , |
u 2gh2 |
|||
Следовательно: |
|
|
||
|
u |
|
|
h2 |
|
(10) |
|
V |
h1 |
||||||
|
|
|
|
|
Но:
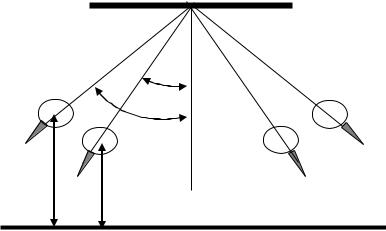
h1 R(1 cos ) , |
h2 R(1 cos ) , |
(11) |
|||
где: R - длина нити, - угол отклонения после удара, |
|||||
- угол отклонения до удара. |
|
||||
Подставляя (11) в (10), окончательно получим: |
|
||||
|
|
|
|
|
|
|
|
1 cos |
|
|
(12) |
|
|
1 cos |
|
|
|
Работа деформации определяется из уравнения (5), в котором кинетические энергии заменяются потенциальными, а высоты через углы по формулам (11). После подстановки окончательно получим:
A 2mgR(cos cos ) (13)
Измерения и обработка результатов
1.Ознакомиться с установкой. Убедиться в одинаковости длин нитей подвесок и при необходимости отрегулировать их.
2.Выполнить измерения. Для этого отвести шары на одинаковые углы ( ) и заметить углы их наибольшего отклонения ( ) после первого удара.
3.Провести опыты с другими значениями . Для каждого отклонения провести опыты по три раза.
4.Выполнить расчеты и A по формулам (12) и (13).
5.Оценить погрешность измерения. Результаты измерений и расчетов занести в таблицу.
Значения масс шаров и длины нитей берутся из таблички на установке.
Данные опытов занести в таблицу:
6
№ |
|
|
|
|
|
|
|
|
ср |
|
опыта |
m |
R |
A |
|
|
100 |
||||
|
|
|||||||||
|
ср |
|||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
% |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сред. |
|
|
|
|
|
|
|
|
|
|
знач. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы
1.Дать определения абсолютно упругого и абсолютно неупругого ударов.
2.Какие законы сохранения выполняются при этих ударах? Сформулировать их.
3.Какой удар называется центральным?
4.Какими величинами оценивается степень "неупругости" удара?
5.Что называется коэффициентом восстановления и от чего он зависит?
6. По каким результатам проведенных вами исследований можно заключить, является ли удар шаров в лабораторной установке абсолютно упругим или абсолютно неупругим? Как вы назовете этот удар?
Литература
1.Курс общей физики. Том 1. Савельев И.С.
2.Курс физики. Том 1. Яворский Б.М., Детлаф А.А.
3.Курс общей физики. Шубин И.В.
β
α
h 1
h2
Рис.1
7
ЛАБОРАТОРНАЯ РАБОТА №2
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА И СИЛЫ ТРЕНИЯ В ОПОРЕ
Цель работы: Закрепление теоретического материала по теме "Динамика вращательного движения твердого тела".
Задачи: Вычислить момент инерции махового колеса и силу трения в опоре. Приборы и принадлежности: Прибор, состоящий из махового колеса,
укрепленного на стене, масштабная линейка, штангенциркуль, секундомер, шнур с грузом.
Краткая теория
Твердое тело можно рассматривать как систему материальных точек, расстояние между которыми неизменно. Вращательным движением твердого тела называют такое движение, при котором все точки тела описывают окружности вокруг некоторой оси вращения. Если тело может вращаться вокруг неподвижной оси, то изменение его движения зависит от действующего на тело момента силы. Моментом силы M относительно неподвижной оси называется векторная физическая величина, численно равная произведению силы F на её плечо , т.е. кратчайшее расстояние от оси вращения до прямой, вдоль которой действует сила:
F (1)
Вращательное движение твердого тела характеризуется угловой скоростью |
||
и угловым ускорением . |
|
|
|
|
|
Угловой скоростью вращения называется вектор , численно равный |
||
первой производной от угла поворота |
|
радиуса-вектора по времени и |
направленный вдоль оси вращения так, |
что |
из его конца вращение видно |
происходящим против часовой стрелки: |
|
|
d |
(2) |
|
dt
Угловым ускорением называется вектор , равный первой производной от угловой скорости по времени:
d |
(3) |
dt
8
Моментом инерции материальной точки относительно оси вращения называют скалярную физическую величину, численно равную произведению массы этой точки на квадрат расстояния её до оси вращения:
|
i |
m r2 |
(4) |
|
i i |
|
Момент инерции твердого тела равен сумме моментов инерций материальных точек:
|
n |
|
|
|
|
|
m r2 |
|
(5) |
|
|
||
|
i |
i |
|
|
|
|
|
i 1 |
|
|
|
|
|
|
Зависимость углового ускорения от момента M |
|||||
|
|
действующей на тело силы и момента инерции |
||||
|
|
тела выражается вторым законом Ньютона |
||||
|
mi |
|
для вращательного движения (основным |
|||
r1 |
|
|
законом динамики вращательного |
|||
|
|
|
движения): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1 |
|
M |
(6) |
и читается: |
||
|
|
|
|
|
|
|
угловое ускорение тела при его вращении вокруг неподвижной оси
прямо пропорционально вращающему моменту М силы, действующей на тело, и обратно пропорционально моменту инерции І тела относительно этой оси.
Если сопоставить законы поступательного и вращательного движений, легко сделать вывод, что момент инерции во вращательном движении выполняет ту же роль, что и масса в поступательном движении, так момент инерции характеризует инертность тела во вращательном движении.
Вращающееся тело обладает кинетической энергией:
Wвр |
|
|
2 |
2 |
(7) |
||
|
|
|
Момент инерции махового колеса и силу трения вала в опоре можно определить при помощи прибора, изображенного на рисунке 2.
9
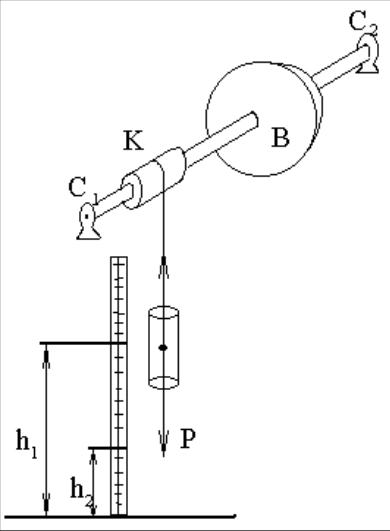
Рис. 2
Прибор состоит из махового колеса B, укрепленного на валу. Вал установлен на шарикоподшипникахC1 и C2 . Маховое колесо приводится во вращательное
движение грузом Р. Груз Р на какой - то высоте h1 обладает потенциальной
энергией mgh 1 , где m масса груза.
Если предоставить возможность грузу падать, то потенциальная энергия mgh1
|
|
m V 2 |
|
|
||
груза перейдет в кинетическую энергию |
|
|
поступательного движения груза, |
|||
2 |
||||||
|
|
|
|
|||
кинетическую энергию вращательного движения |
I 2 |
прибора и в работу |
||||
2 |
||||||
|
|
|
|
|
||
А f h по преодолению силы трения f |
в опоре. По закону сохранения энергии |
|||||
10
mgh |
m V 2 |
|
I 2 |
fh |
(8) |
|
|
||||
1 |
2 |
|
2 |
1 |
|
|
|
|
|
Движение груза - равноускоренное без начальной скорости, поэтому ускорение а и скорость V соответственно равны:
a 2 h1 |
; V 2 h1 , |
(9) |
t 2 |
t |
|
где t - время опускания груза с высоты h1.
Найдем угловую скорость махового колеса по формуле:
|
V |
2 h1 , |
(10) |
|
|
|
r |
t r |
|
где r - радиус вала, на который намотана нить. |
|
|||
Сила |
трения f вычисляется |
следующим |
образом. После опускания груза |
|
колесо, |
вращаясь по инерции, |
поднимает |
груз на высоту h2 h1 , и |
|
потенциальная энергия груза на высоте h2 будет равна mgh2 .
Уменьшение потенциальной энергии при подъеме груза равно работе по преодолению силы трения в опорах С1 и С2 , т. е.
mgh1 mgh2 f (h1 h2 ) ,
отсюда |
|
|
f mg h1 |
h2 |
(11) |
h1 |
h2 |
|
Подставляя в формулу (8) значения V, |
и f из (9), (10) и (11) получим |
|
окончательное выражение для вычисления момента инерции махового колеса:
I mr2 (g t2 |
h2 |
1) |
(12) |
|
h1 (h1 h2 ) |
||||
|
|
|
Порядок выполнения работы.
1.Наматывая на шкив шнур, поднять груз на высоту h1 .
2.Отпустить груз и секундомером измерить время падения груза с высоты h1 .
11
3.Определить высоту h2 , на которую поднимается груз после опускания.
4.Измерить штангенциркулем радиус шкива r и вычислить момент инерции махового колеса и силу трения в опоре по формулам (12) и (11). Полученные
результаты занести в таблицу. Повторить опыты при других значениях h1 или массы m груза.
|
|
|
|
|
|
|
|
|
|
|
|
№ |
r |
m |
h1 |
h2 |
t |
f |
I |
|
|
Е,% |
Е,% |
опыта |
|
|
|
f |
I |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы
1.Что называют моментом инерции материальной точки, твердого тела относительно оси вращения? В каких единицах измеряется?
2.Что называется моментом силы относительно оси вращения?
Как записывается основной закон динамики для вращательного движения?
3.Чему равна кинетическая энергия вращающегося тела?
4.Как определить линейное ускорение груза и угловое ускорение колеса?
5.Какой закон положен в основу вывода расчетных формул?
Литература
1.Курс общей физики. Том 1. Савельев И.С.
2.Курс физики. Том 1. Яворской Б.М., Детлаф А.А.
3.Курс общей физики. Шубин И.В.
12
