
ЧАСТЬ 1
.pdf
ЛАБОРАТОРНАЯ РАБОТА №3
ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА ПО РАСТЯЖЕНИЮ ПРОВОЛОКИ
Цель работы: практическое изучение закона Гука.
Задача: определить практически модуль Юнга по растяжению стальной проволоки.
Приборы и принадлежности: 1.Стальная проволока
2.Микроскоп отсчетный "МИР".
3.Микрометр.
4.Грузы.
Краткая теория
Сила характеризует действие одного тела на другое. В результате этого воздействия тело может прийти в движение или деформироваться. Деформацией твердого тела называется изменение взаимного расположения частиц тела, которое приводит к изменению формы и размеров тела и вызывает изменение сил взаимодействия между частицами, т. е. возникновение напряжений. Деформируемыми являются все вещества.
Деформация может быть следствием теплового расширения, воздействия электрических и магнитных полей, а также внешних механических сил.
В твердых телах деформация называется упругой, если она исчезает после снятия нагрузки, и пластической, если она после снятия нагрузки не исчезает.
Внутри деформированного тела возникает противодействующая сила, равная по величине деформирующей силе и называемая силой упругости. Силы упругости обусловлены взаимодействием между частицами (молекулами и атомами) тела и имеют электрическую природу.
Физическая величина, численно равная упругой силе dFупр , приходящейся на единицу площади dS сечение тела, называется напряжением:
dFупр
dS
Английский физик Р. Гук экспериментально установил, что напряжение |
|||||||
|
при упругих деформациях |
тела |
прямо |
пропорционально |
его |
||
относительной деформации : |
|
|
|
|
|
||
|
E , |
(1) |
|
|
|
|
|
где |
Е - модуль Юнга (модуль упругости), |
величина |
которого определяется |
||||
|
|
|
|
11 |
Н |
|
|
свойствами материала, из которого изготовлено тело. Например, Естали 2 10 |
|
; |
|||||
м2 |
|||||||
|
|
|
|
|
|
||
|
|
13 |
|
|
|
|
|
Ешелк 6 10 |
|
Н |
; |
Ерезина 4 10 |
9 Н |
; |
Естекло |
7,2 10 |
Н |
. |
||
|
9 |
|
|
|
|
|
10 |
|
||||
|
|
м2 |
|
|
|
м2 |
|
|
|
|
м2 |
|
Относительная деформация равна отношению абсолютной деформации L |
||||||||||||
к начальной длине L : |
|
|
|
|
L |
|
|
|
||||
|
|
|
|
|
|
|
(2) |
|
|
|||
|
|
|
|
|
|
|
|
|
||||
L
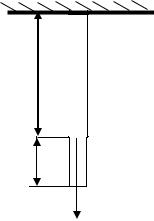
Рассмотрим упругую деформацию одностороннего растяжения проволоки
(рис. 1 )
L |
L |
|
F |
Рис. 1 |
К нижнему концу закрепленной проволоки длиной L и площадью поперечного сечения S приложим силу F , под действием которой проволока получит абсолютное удлинение L
и в ней возникнет сила упругости F1 F . По закону Гука напряжение , возникшее в
проволоке, прямо пропорционально относительной деформации:
E (1) ,
отсюда модуль Юнга равен:
Е = |
(2) |
Если положить, что L L , т.е. 1, то E , т.е. модуль Юнга численно
равен напряжению, возникающему в упруго деформированном теле, при относительной деформации, равной единице.
Заменив в формуле (2) напряжение и относительное удлинение по формулам
F |
и L , получим: |
S |
L |
E |
FL |
(3) |
|
|
|
S L |
|
|
|||
|
|
|
|
|
|
Площадь поперечного сечения |
проволоки S |
d |
2 |
||
4 |
(4), где d диаметр |
||||
|
|
|
|
|
|
проволоки. |
|
|
|
|
|
Подставив выражение (4) в (3) |
и учитывая, что |
F mg , получим расчетную |
|||
формулу для модуля Юнга:
14
E |
4F L |
4mg L |
(5) |
|
|||
|
d 2 L |
d 2 L |
|
Порядок выполнения работы
1.Отметим на исследуемой проволоке какую-нибудь точку, для чего укрепим на ней кусочек тонкой проволоки.
2.Наведем на эту точку отсчетный микроскоп и заметим деление n0 на шкале
микроскопа, которое совпадает с указанной точкой. После этого кладем на чашку груз массой m1.
3.Определяем удлинение проволоки, вызванное нагрузкой F1 m1g ,
L1 k(n1 n0 )
Здесь k пересчетный коэффициент измерительного микроскопа, переводящий удлинение в делениях шкалы, видимой в окуляре, в миллиметры. Каждому значению длины тубуса микроскопа соответствует свое значение k , которое указано в таблице на установке.
4.Вычисляем модуль Юнга по формуле (5), значение d и L указаны на табличке возле установки.
5.Опыты повторить с другими значениями масс m2 , m3 .
6.Результаты опытов занести в таблицу:
|
|
|
|
|
|
|
№ L d K m |
n0 |
n L |
E E |
E |
E |
E |
опыта |
|
|
cp |
|
cp |
ист |
1
2
3
Контрольные вопросы
1.Что называется деформацией, виды деформаций?
2.Какими величинами характеризуют деформацию растяжения (сжатия)?
15
3.Как читается закон Гука и для каких деформаций он справедлив? 4.Какой физический смысл модуля Юнга?
Литература.
1.Детлаф А.А., Яворский Б.М., Милковская Л.Б. "Курс физики" ч.1.
2.Шубин А.С. "Курс общей Физики".
3.Грабовский Р.И. "Курс физики".
16
ЛАБОРАТОРНАЯ РАБОТА № 4
ОПЫТНАЯ ПРОВЕРКА УРАВНЕНИЯ БЕРНУЛЛИ
Цель работы: Изучить законы стационарного движения жидкости.
Задача: Проверить опытным путем уравнение Бернулли, вычислив экспериментально и теоретически расход жидкости.
Краткая теория
Раздел физики, в котором рассматривают законы равновесия и движения жидких и газообразных тел, а также их взаимодействия с твердыми телами,
называют гидроаэромеханикой.
Характерное свойство жидких и газообразных тел – их текучесть, т.е. малая сопротивляемость деформации сдвига: если скорость сдвига стремится к нулю, то силы сопротивления жидкости или газа этой деформации также стремятся к нулю. Иными словами, жидкие и газообразные тела не обладают упругостью формы – они легко принимают форму того сосуда, в котором находятся. Вследствие этого внешнее давление, производимое на жидкость или газ, передается ими во все стороны равномерно (закон Паскаля).
Движение жидкостей или газов называют течением, а совокупность частиц движущейся жидкости или газа называют потоком. В гидромеханике отвлекаются от молекулярного строения жидкостей и газов, рассматривая их как сплошную среду.
Течение жидкости называют установившимся или стационарным, если скорость жидкости в каждой точке пространства, занятого жидкостью, не изменяется с течением времени, т.е. V не зависит от t. В случае неустановившегося течения V зависит также от времени t.
Течение называют ламинарным или слоистым в том случае, если поток представляет собой совокупность слоев, перемещающихся друг относительно друга без перемешивания. Течение называют турбулентным, если имеет место перемешивание различных слоев жидкости или газа вследствие образующихся завихрений.
Вцелях наглядности движение жидкости можно изображать с помощью линий тока, которые проводят так, что касательные к ним совпадают по направлению с векторами скоростей жидкости в соответствующих точках пространства. В случае стационарного течения линии тока не изменяются с течением времени и совпадают с траекториями отдельных частиц жидкости.
Поверхность, которая образована линиями тока, проведенными через все точки малого замкнутого контура, называют трубкой тока. Часть жидкости, ограниченную трубкой тока, называют струей.
Вреальных жидкостях течение усложняется тем, что между отдельными слоями потока происходит внутреннее трение. Однако в ряде случаев влияние
17
внутреннего трения невелико и им можно пренебречь. Жидкость, в которой отсутствует внутреннее трение, называют идеальной жидкостью. Поэтому изучая движение идеальной жидкости, можно установить ряд закономерностей, которые с известным приближением применимы к течению реальных жидкостей.
При переходе потока жидкости из трубки с большим диаметром Д 1 в трубку с
меньшим диаметром Д 2 происходит увеличение скорости течения от значения V
1 до значения V 2 . Соотношение между скоростями течения V 1 |
и V 2 задается |
|||||
уравнением неразрывности струи: |
SV = Const |
|
|
|
||
или для двух сечений: S 1 V 1 =S 2 V 2 |
(1) |
|
|
|
||
|
Д 2 |
|
2 |
= V 2 Д |
2 |
|
Если S= |
4 |
, то уравнение (1) перепишется: V 1 Д 1 |
2 |
(2) |
||
|
|
|
|
|
|
|
Изменение скорости течения влечет изменение давления, которое можно определить из уравнения Бернулли:
V 2 |
|
|
|
V 2 |
|
|
|
1 1 |
gh P |
2 |
2 |
gh |
|
P |
|
|
|
|
2 |
||||
2 |
1 |
1 |
2 |
|
2 |
||
|
|
|
|
|
|||
Для горизонтальной трубки уравнение Бернулли запишется:
|
V 2 |
P |
|
V 2 |
|
P |
|
|
||||||||||||||
|
|
1 |
1 |
|
2 2 |
|
, отсюда |
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2 |
|
|
|
1 |
|
|
|
|
2 |
|
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
(V |
2 V 2 ) |
, |
|
|
|
|
||||||
P |
|
- P |
|
|
= |
|
|
|
|
|
|
(3) |
||||||||||
1 |
2 |
2 |
|
2 |
|
1 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Где P1 , V 1 |
|
и |
|
P 2 , |
|
V 2 |
- давления и скорости в сечениях Д 1 и Д 2 |
|||||||||||||||
соответственно; - плотность жидкости. |
||||||||||||||||||||||
|
|
Решая совместно уравнения (2) и (3), найдем скорость течения V 2 : |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
2(P1 P2 ) |
|
|
|
|
|
|
|||||||||
V 2 = |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
(4) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Д2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
|
Д1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Воспользовавшись уравнением неразрывности струи, найдем секундный объемный расход жидкости:
18
Wтеор S2V2 |
Д 2 |
|
2(P P ) |
|
|
|
|||||
|
|
|
|
1 |
2 |
|
|
|
|
||
4 |
|
|
|
|
|
|
|
4 |
(5) |
||
|
|
|
|
|
Д2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
Д1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
Экспериментально секундный объемный расход жидкости можно определить, измеряя время t наполнения жидкостью баллона объемом V:
W Э = |
V |
(6) |
|
t |
|||
|
|
Сравнение результатов измерений секундного объемного расходов жидкости, полученным по формулам (5) и (6), может служить проверкой справедливости уравнения Бернулли.
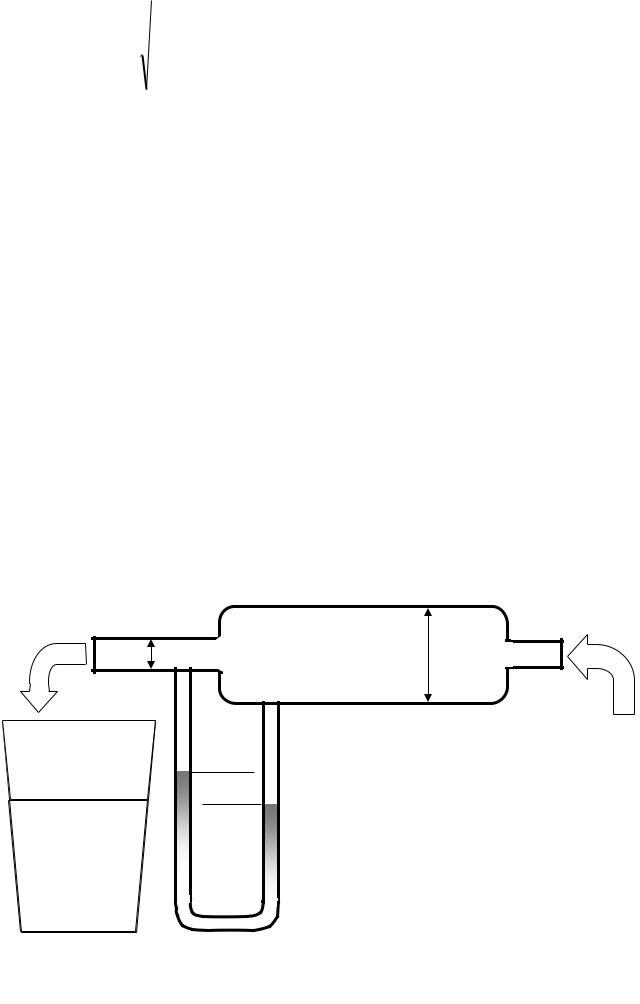
Описание установки
На деревянной подставке закреплена стеклянная трубка переменного сечения. Диаметры узкой и широкой части трубки указаны на табличке возле установки.
Резиновая трубка соединяет прибор с водопроводным краном, а другая служит для слива воды.
Разность давлений, создаваемая струей жидкости, имеющей скорость V 1 в
широкой части и скорость V 2 в узкой части, измеряется при помощи ртутного или водяного манометра. Трубка должна иметь горизонтальное положение.
Схема установки с ртутным манометром
Д1
Д2
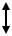 h
h
V
V
19
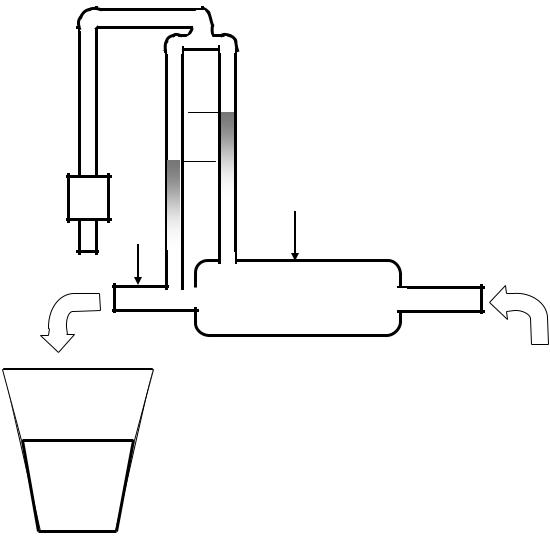
Схема установки с водяным манометром
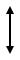 h
h
K |

 Д1
Д1 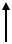 Д2
Д2 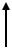
V
V
Порядок выполнения работы
1. Через прибор пропускается вода из водопровода и измеряется разность уровней h в коленах манометра.
В формуле (5) разность давлений (P 1 - P 2 ) заменим по формулам:
P 1 |
- P 2 |
= ( 2 - 1 )gh |
(для ртутного манометра) |
и |
|
|
|
P 1 |
- P 2 |
= 1 gh |
(для водяного манометра) |
И получим формулы для расчета теоретического значения расхода жидкости: - в установке с ртутным манометром:
20

|
Д2 |
|
2gh( 2 |
1 ) |
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
4 |
W |
|
|
|
|
|
|
|
|
|
|
Д 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
теор |
4 |
|
|
|
|
|
4 |
|
или так как Д 1 >> Д 2 |
и |
|
|
0 |
|
|
|
|
|
|
||||||||
|
|
|
|
Д2 |
|
|
|
|
|
Д1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Д1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д22 |
|
2 |
|
Wтеор |
|
|
|
|
|
|
|
||||
4 |
2gh |
1 |
1 |
||
|
|
|
|
- в установке с водяным манометром:
|
|
|
|
|
|||
WТЕОР |
Д 2 |
|
2gh |
|
|
||
2 |
|
|
|
|
|
|
|
4 |
|
|
|
Д 2 |
4 |
|
|
|
1 |
|
|
|
|||
|
|
|
|||||
|
|
|
|
|
Д1 |
|
|
|
|
|
|
|
|
|
|
2.При помощи секундомера измерить время, в течение которого наполняется водой сосуд объемом V.
3.Рассчитать экспериментальный расход воды по формуле (6):
WЭ Vt
4.Измерения провести для разных значений h.
5.Результаты измерений и вычислений занести в таблицу:
|
|
|
|
|
|
|
|
|
|
|
№ |
V |
h |
t |
W Э |
Д 1 |
Д |
|
W |
|
W |
опыта |
|
|
|
2 |
т |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21
Контрольные вопросы
1.Дать понятие идеальной жидкости.
2.Записать и сформулировать теорему неразрывности струи.
3.Записать и сформулировать уравнение Бернулли.
4.Как вы в работе проверяли справедливость уравнения Бернулли?
Литература
1.Б.М. Яворский, А.А. Детлаф “Курс физики” т.1
2.А.С. Шубин “Курс общей физики”
22
