ЧАСТЬ 1

Каждая молекула газа участвует в двух движениях: хаотическом тепловом со

средней скоростью u и упорядоченном движении со скоростью V. Вследствие хаотического теплового движения происходит непрерывный переход молекул из одного слоя в другой

Попав в другой слой, молекула сталкивается с молекулами этого слоя, в результате чего она либо отдает избыток своего импульса другим молекулам (если она прилетела из слоя, движущегося с большей скоростью), либо увеличивает свой импульс за счет других молекул (если она прилетела из слоя, движущегося с меньшей скоростью). В итоге импульс более быстро движущегося слоя убывает, а более медленно движущегося возрастает. Слои ведут себя так, как если бы к первому слою (скорость которого больше) была приложена тормозящая его движение сила, а ко второму слою (скорость которого меньше) – такая же по величине ускоряющая сила.

Теория метода

Для измерения коэффициента динамической вязкости воздуха в данной работе используется метод Пуазейля (метод основан на определении скорости

истечения жидкости или газа через капилляр). Если открыть кран К 1 , то

вследствие вытекания воды из баллона давление воздуха будет уменьшаться и в него будет через капилляр засасываться воздух. Объем V газа, протекающего через капиллярную трубку радиуса r за время t, определяется по формуле Пуазейля:

Здесь g – ускорение свободного падения, h – разность столбов жидкости в

Средняя арифметическая скорость V молекул определяется по формуле:

Плотность газа можно найти, воспользовавшись уравнением состояния газа:

где P и T – давление и температура газа.

Решая совместно уравнения (2), (3) и (4), получим формулу для расчета

средней длины свободного пробега молекул газа:

где R – универсальная газовая постоянная;

- молярная масса газа (для воздуха 29 10 3 молькг );

P – давление газа (в условиях данной задачи его можно считать равным 10 5 Па)

Из молекулярно-кинетической теории известно, что

Отсюда найдем эффективный диаметр молекулы газа:

где k – постоянная Больцмана.

Порядок выполнения работы.

1.Открыть кран К 1 , подставив под него запасной стаканчик, и выждать пока установится стационарное течение (при этом разность уровней в манометре будет постоянной.

2.Измерить эту разность уровней h 1 .

3.Заменить запасной стаканчик мерным, включить секундомер и измерить время заполнения мерного стаканчика (50 или 100 см 3 ).

4.Снова измерить разность уровней h 2 в манометре.

5.По формулам (1), (5) и (6), используя программу, рассчитать коэффициент

внутреннего трения, среднюю длину свободного пробега и эффективный диаметр молекул газа.

34

6.Опыт повторить 3 раза.

7.Результаты измерений и вычислений занести в таблицу.

8.Включив нагреватель (с разрешения преподавателя), повторить пункты (1-5) при температурах выше комнатной.

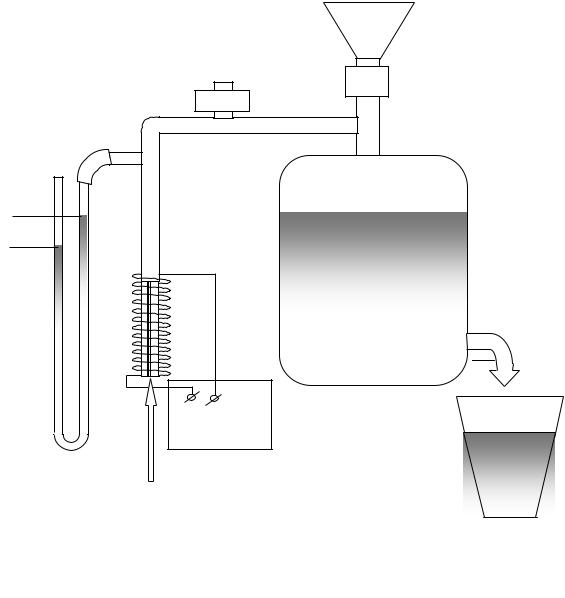
Схема установки

h

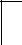
К1

Источник

питания

V

Капилляр

Рис.1

35

Таблица

Контрольные вопросы.

1.Объясните механизм возникновения силы внутреннего трения в газе. 2.Запишите и поясните закон Ньютона.

3.В чем состоит метод Пуазейля, запишите и поясните формулу Пуазейля. 4.Дайте определения коэффициента внутреннего трения, средней длины свободного пробега и эффективного диаметра молекул газа?

5.От чего зависит коэффициент внутреннего трения газа?

Литература

1.Савельев И.В. “Курс общей физики”, Т.1

2.Шубин А.С. “Курс общей физики”

3.Грабовский Р.П. “Курс физики”

36

ЛАБОРАТОРНАЯ РАБОТА № 8

ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ УДЕЛЬНЫХ ТЕПЛОЕМКОСТЕЙ

Приборы и принадлежности: стеклянный баллон, манометр, насос.

Цель работы: определение показателя адиабаты (коэффициента Пуассона)

методом Клемана-Дезорма для воздуха.

Теория метода и описание установки.

Удельной теплоемкостью С газа называется скалярная физическая величина, численно равная количеству теплоты Q, которое необходимо сообщить единице массы газа, чтобы увеличить его температуру на 1 К:

Величина теплоемкости газов зависит от условий нагревания. Выясним эту зависимость, воспользовавшись первым законом термодинамики, который гласит: количество теплоты Q, сообщенное системе, затрачивается на увеличение ее внутренней энергии U и на работу А, совершаемую системой

против внешних сил

Q U A (2)

При изохорическом (V=const) нагревании газа V 0 , следовательно, и А=0. Тогда все подводимое к газу тепло идет на увеличении его внутренней энергии:

Q U

Из формулы (1) следует, что

CV U (3) m T

При изобарном (Р=const) нагревании газа тепло, сообщаемое газу идет и на увеличение внутренней энергии и на совершение газом работы против внешних сил:

В частности оно входит в уравнение Пуассона, которое описывает адиабатическое расширение газа

В данной работе прелагается один из самых простых методов определения C p -

Cv

метод Клемана и Дезорма. Адиабатическим процессом называется процесс, протекающий без теплообмена с окружающей средой, т.е. считается, что процесс передачи тепла системе от окружающей среды отсутствует.

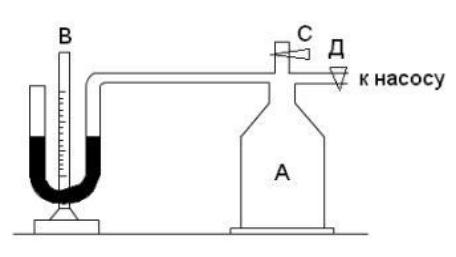
Экспериментальная установка состоит из стеклянного баллона А (рис. 1), соединенного с манометром В и с насосом.

Рис. 1

Если про помощи насоса накачать в баллон некоторое количество воздуха, то давление и температура воздуха внутри баллона повысятся. Вследствие теплообмена воздуха с окружающей средой через некоторое время температура воздуха, находящегося в баллоне, сравнятся с температурой внешней среды T1 .

Давление, установившееся в баллоне

P1 P вН ,

где Р - атмосферное давление; Н - разность уровней жидкости в манометре;

В - коэффициент перехода от разности уровней к давлению.

Таким образом, состояние воздуха внутри баллона, которое назовем 1 состоянием, характеризуется параметрами

P P вН ; V и T

1 1 1

Если на короткое время открыть кран С, то воздух в баллоне будет расширяться. Этот процесс расширения можно считать адиабатическим. Давление в баллоне установится равным атмосферному Р, температура газа понизится до T 2

, а объем будет равен V 2 .

Следовательно, в конце адиабатического процесса, что назовем 2 состоянием, параметры состояния газа будут Р; V 2 ,T 2 .

38

Применяя к 1 и 2 состояниям уравнение (5), получим:

Охладившийся при адиабатическом расширении воздух в баллоне через некоторое время вследствие теплообмена нагреется до температуры внешней среды T1 , давление возрастет до некоторой величины

P2 P вh ,

где h- новая разность уровней в манометре.

Объем воздуха не изменится и будет равен V2 .

Это состояние воздуха, которое назовем 3 состоянием, характеризуется параметрами

P2 P вh ; V2 ; T1

Так как в состояниях 1 и 3 воздух имеет одну и ту же температуру T1 (процесс изотерический), то, применяя закон Бойля-Мариотта (PV=const), получим:

(P+вH)V1 (P+вh)V2

Логарифмируя это выражение и решая относительно , находим

Так как давления Р, Р+вН и Р+вh мало отличаются друг от друга, то разности логарифмов можно принять пропорциональными разностям самих давлений и приближенно положить

Таким образом, экспериментальное определение C p сводится к измерению H и

Cv

h, то есть формула (8) является расчетной формулой для определения коэффициента Пуассона

39

Порядок выполнения работы

1.Открыть кран Д, при закрытом кране С накачать воздух в баллон так, чтобы разность уровней жидкости в манометре составила 30-40 мм.

2.Закрыть кран Д и выждать 2-3 минуты, пока благодаря теплообмену температура в баллоне не станет равной комнатной, и уровни в коленах манометра перестанут изменяться.

3.Отсчитать разность уровней Н жидкости в коленах манометра.

4.Открыть кран С и в тот момент, когда уровни жидкости обоих коленах манометра сравняются, быстро закрыть кран С.

5.Выждать 2-3 минуты пока газ, охлажденный про адиабатическом расширении, нагреется до комнатной температуры T1 и отсчитать разность

уровней h жидкости в коленах манометра.

6.По формуле (8) вычислить значение .

7.Опыт повторить 5-7 раз, меняя величину Н.

Все полученные опытом (и вычислением) результаты измерений занести в таблицу отчета.

Контрольные вопросы

1.Что называется удельной теплоемкостью?

2.Запишите и сформулируйте I начало термодинамики

3.Почему C p Cv ?

4.Какой процесс называется адиабатическим? Запишите уравнение Пуассона.

5.Почему температура газа при адиабатном расширении уменьшается?

40

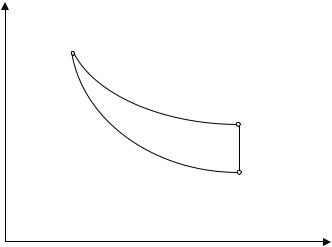
P

1(P1 ,V1 ,T1 )

3(P 2 ,V 2 ,T1 )

2(P,V 2 ,T 2 )

V

Рис. 2

Литература

1.Шубин А.С. Курс общей физики.

2.Савельев И.В. Курс физики, т.1

3.Детлаф А.А., Яворский Б.М. Курс физики, т.1.

41