Рассмотрим методику решения задач квадратичного программирования с помощью winqsb.

Решим пример 9.4.

Для решения надо выполнить следующие действия.

1. Включить компьютер.

2. Найти и открыть папку WINQSB.		3. Загружаем файл QP-IQP (Квадратичное программирование)	4. Активизируем курсором файл

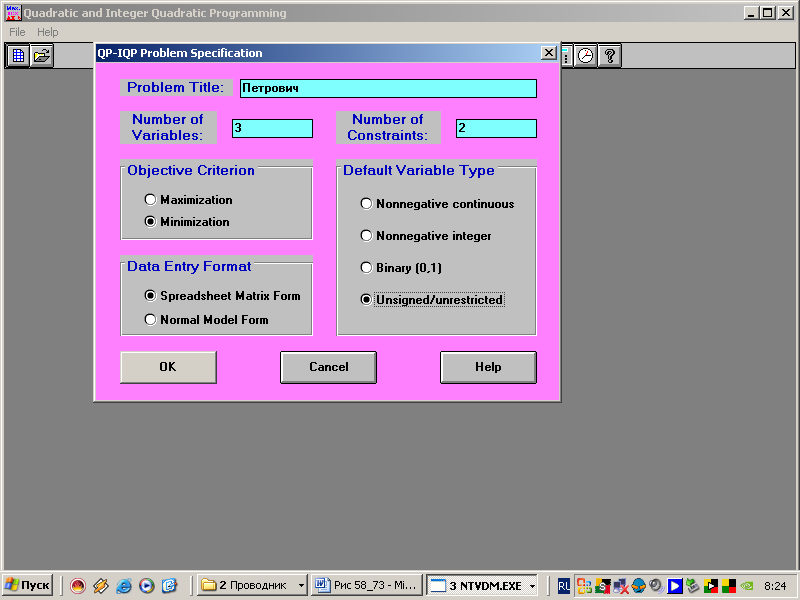
5. В появившуюся таблицу вносим данные:

• Имя проблемы, например Петрович;

• Количество переменных, в нашем примере 3;

• Количество ограничений, в нашем примере 2;

• Курсором устанавливаем Manimization, так как наша задача на min;

• OK.

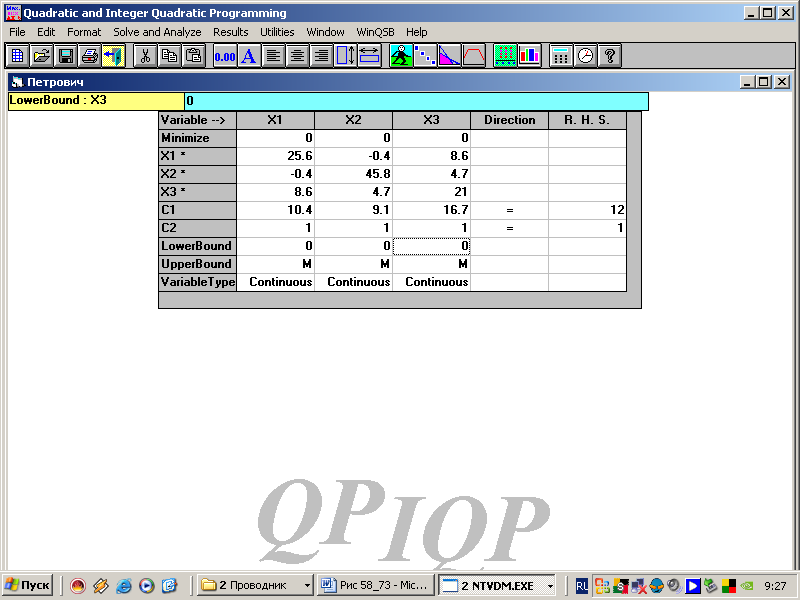
6. Вводим числовые данные в таблицу 9.19.

Таблица 9.19

Последовательно выполняем действия.

7.

8.

9.

10. Получили решение в виде таблицы

Таблица 9.20

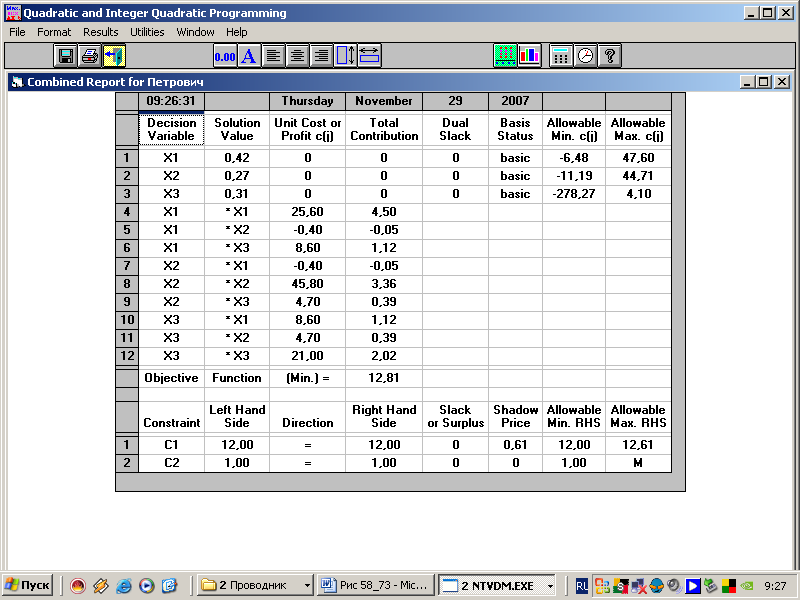
Структура оптимального портфеля: .

Контрольные задания

Задание 1. Составить математическую модель задачи линейного программирования

1. Для приобретения оборудования выделены 20 тыс. грн. Оборудование необходимо разместить на площади не более чем на 38м². Предприятие может заказать оборудование двух типов – А и В по такими данными: единица А – стоимостью 5 тыс. грн. требует площадь 8м² и выпускает продукции на 7 тыс. грн. за смену; единица В – стоимостью 2 тыс. грн. требует площадь 4м² и выпускает продукции на 3 тыс. грн. за смену.

Сколько оборудования каждого типа нужно приобрести, чтобы получить максимальную общую выручку (ограничиться составлением математической модели)?

2. Необходимо распределить площадь посева под пшеницу и ячмень таким образом, чтобы получить максимальное количество продукции в стоимостном выражении, если известная урожайность, цена, а также расходы ресурсов механизированного и ручного труда на один гектар посева и общая величина ресурсов:

Вид ресурсов	Нормы расходов на 1 га		Общий объем ресурсов
	Пшеница	Ячмень
Механизированный труд, час./га	1,2	1,5	5500
Ручной труд, час./га	2,1	1,9	5000
Урожайность ц/га	30	22
Цена 1ц продукции, грн	50	30

Ограничиться составлением математической модели.

3. Две торговые базы обеспечивают четыре магазина мукой. Известные транспортные расходы на перевозку муки от каждой базы к каждому магазину, коп/кг.

Резервы баз, кг	Объем потребностей магазинов, кг
	900	800	1200	1100
1900	3	4	2	3
2200	2	5	1	4

Определить план закрепления магазинов за базами, чтобы транспортные расходы были минимальные (ограничиться составлением математической модели).

4. Четыре экскаватора могут работать в четырех карьерах. Производительность усл. ед. каждого внесена в таблицу:

Карьер Экскаватор	1	2	3	4
1	40	30	60	50
2	40	30	60	20
3	30	60	60	10
4	50	60	60	50

Каждый экскаватор может быть направлен лишь в один карьер. Составить оптимальный план направления экскаваторов (ограничится составлением математической модели).

5. Пищево-вкусовая фабрика выпускает фруктовый сок в стеклянной, металлической и полиэтиленовой таре. Производительность линии по выпуске сока составляет: в стеклянной таре не более 10т, в металлической – не более 8т, в полиэтиленовой таре – не более 5т. Известно, что себестоимость производства 1т сока в стеклянной таре равна 1600грн., в металлической – 1000грн., в полиэтиленовой – 1500грн. Отпускная цена не зависит от тары и равняется 4тыс. грн. за 1т. Определить программу выпуска сока в разной таре, которая обеспечивала бы максимальную прибыль (ограничится составлением математической модели).

6. В микрорайоне планируется строить дома четырех типов. Данные о количестве квартир в доме каждого типа, потребности в квартирах и стоимость домов внесены в таблицу:

Типы домов Типы квартир	Д-1	Д-2	Д-3	Д-4	Потребности квартир
Четырехкомнатные	20	10		5	2000
Однокомнатные	10	18	20	60	3000
Трехкомнатные	60	90	10	0	4000
Двухкомнатные	40	20	60	30	6000
Стоимость дома (усл. ед)	10	10	5	8

Найти план застройки микрорайона. Ограничиться составлением математической модели.

7. Нефтеперерабатывающий завод производит за месяц 1,5млн. л. алкилата, 1,2млн. л. крекинг-бензина и 1,3 млн. л. изопентана. В результате смешивания этих компонент в пропорциях 1:1:1 и 3:1:2 получается бензин сорта А и В соответственно. Стоимость 1000 л бензина сорта А и В соответственно равняется 4000грн. и 4200грн. Определить месячный план выпуска бензина сорта А и В с целью максимизации стоимости выпущенной продукции.(ограничиться составлением математической модели).

8. Необходимо распределить площадь посева под пшеницу и ячмень таким образом, чтобы получить максимальное количество продукции в стоимостном выражении, если известная урожайность, цена, а также расходы ресурсов механизированного и ручного труда на один гектар посева и общая величина ресурсов.

Вид ресурсов	Нормы расходов на 1 га		Общий объем ресурсов
	Пшеница	Ячмень
Механизированный труд, час./га	1,6	1,2	4000
Ручной труд, час./га	2,3	1,3	5000
Урожайность ц/га	35	20
Цена 1ц продукции, грн	70	50

Ограничиться составлением математической модели.

9. Рацион стада крупного рогатого скота с 220 голов включает питательные вещества А,B,C,D,E. Ежедневно каждое животное должно съедать питательных веществ каждого вида не меньше: 1.9кг – А, 1,6кг – В, 1.1кг – С, 2.5кг – D и 1,5кг вида Е. Но в чистом виде указанные вещества не производятся. Они содержатся в концентратах К–1, К–2, К–3. Их цены составляют соответственно 0,5; 0,б4 и 0,9 грн. за кг. Содержание питательных веществ в килограмме концентрата (%) указано в таблице.

Концентраты	Продукты
	А	B	C	D	E
К – 1	18	20	3	0	7
К – 2	16	18	2	24	3
К – 3	6	11	18	6	9

Построить математическую модель минимизации расходов на покупку концентратов для рационального кормления животных.

10. Перед проектировщиками автомобиля поставленная задача разработать наиболее дешевую конструкции кузова, используя листовой металл, стекло и пластмассу. Основные характеристики материала представлены в таблице. Общая поверхность кузова (вместе с дверями и стеклами должна составлять 14м²; из них не меньше 4м² и не больше 5м² нужно отвести под стекло. Масса кузова должна не превосходить 150кг.

Характеристики	Материалы
	Металл	Стекло	Пластмасса
Стоимость, грн./м2	25	20	40
Масса, кг/м2	10	15	3

Сколько металла, стекла и пластмассы должен использовать наилучший проект (ограничиться составлением математической модели)?

11. На заготовительный участок поступили стальные прутья длиной 111см. Необходимо их разрезать на заготовки по 30, 23 и 19см. Последних нужно 190, 215 и 190шт. Найти такой план раскрою прутиков, при котором будет разрезано их минимальное количество (ограничиться составлением математической модели).

12. На заготовительный участок поступили стальные прутья длиной 100см. Необходимо их разрезать на заготовки по 30, 25 и 30см. Последних нужно 200, 100 и 150шт.

Найти такой план раскроя прутиков, при котором будет разрезанный их минимальное количество (ограничиться составлением математической модели).

13. Для приобретения оборудования выделены 40 тыс. грн. Оборудование необходимо разместить на площади не более чем на 50 м². Предприятие может заказать оборудование двух типов – А и В за такими данными: единица А – стоимостью 6 тыс. грн. требует площадь 9м² и выпускает продукции на 8 тыс. грн. за смену; единица В – стоимостью 4тис. грн. требует площадь 5м² и выпускает продукции на 4 тыс. грн. за смену.

Сколько оборудования каждого типа нужно приобрести, чтобы получить максимальную общую выручку (ограничиться составлением математической модели)?

14. Необходимо распределить площадь посева под пшеницу и ячмень таким образом, чтобы получить максимальное количество продукции в стоимостном выражении, если известная урожайность, цена, а также расходы ресурсов механизированного и ручного труда на один гектар посева и общая величина ресурсов.

Вид ресурсов	Нормы расходов на 1 га		Общий объем ресурсов
	Пшеница	Ячмень
Механизированный труд, час./га	1,3	1,6	7600
Ручной труд, час./га	3,1	2,9	7000
Урожайность ц/га	45	30
Цена 1ц продукции, грн	60	40

Ограничиться составлением математической модели.

15. В микрорайоне планируется строить дома четырех типов. Данные о количестве квартир в доме каждого типа, потребности в квартирах и стоимость домов внесены в таблицу:

Типы домов Типы квартир	Д-1	Д-2	Д-3	Д-4	Потребности квартир
Четырехкомнатные	20	10	0	20	2000
Однокомнатные	20	30	50	60	2000
Трехкомнатные	60	100	40	0	4000
Двухкомнатные	20	50	60	20	5000
Стоимость дома (усл. ед.)	20	25	5	10

Найти план застройки микрорайона. Ограничиться составлением математической модели.

16. Рулоны ткани длиной 8,5м нужно разрезать на куски 1,5; 2,4 и 3,2м. Причем кусков по 1,5м необходимо не меньше 25шт., по 2,4м – не меньше 16шт. и по 3,2 – не меньше 30шт.

Определить такой план раскрою ткани, при котором количество разрезанных рулонов ткани было бы минимальным. Ограничиться составлением математической модели.

17. Производственные мощности каждого из пяти заводов позволяют производить лишь пять видов продукции. Данные о выпуске продукции внесены в таблицу

Номер завода Номер продукции	Производительность
	1	2	3	4	5
1	20	14	13	20	13
2	21	21	18	13	12
3	18	14	18	14	21
4	19	16	23	12	13
5	16	19	23	16	21

Определить распределение заказов, чтобы общая производительность была максимальная. Каждый заказ можно заказывать лишь на одном заводе. Ограничиться составлением математической модели.

18. Рацион стада крупного рогатого скота с 150 голов включает питательные вещества А,B,C,D,E. Ежедневно каждое животное должно съедать питательных веществ каждого вида не меньше: 1.9кг – А, 1,6кг – В, 0,8кг – С, 4кг – D и 1,7кг вида Е. Но в чистом виде указанные вещества не производятся. Они содержатся в концентратах К–1, К–2, К–3. Их цены составляют соответственно 0,6; 0,75 и 0,8 грн. за кг. Содержание питательных веществ в килограмме концентрата (%) указано в таблице.

Концентраты	Продукты
	А	B	C	D	E
К – 1	16	20	5	0	5
К – 2	20	18	0	18	11
К – 3	6	15	20	4	9

Построить математическую модель минимизации расходов на покупку концентратов для рационального кормления животных.

19. В металлургическом цехе переплавляют латунь трех видов с содержанием цинка 10, 20, 30, 40% и стоимостью 2, 3, 4, 5 грн. за 1кг соответственно. В каких пропорциях нужно переплавить это сырьё, чтобы получить латунь с 30% содержанием цинка и минимальной ценой за один кг латуни? Ограничиться составлением математической модели.

20. Нефтеперерабатывающий завод изготовляет за месяц 2млн. л алкалита, 2,3 млн. л крекинг- бензина и 1,5 л изопентона. В результате смешивания этих компонентов в пропорциях 1:1:1: и 3:1:2 получают бензин сорта А и В соответственно. Стоимость 1000л бензина сорта А и В соответственно равняется 4200 грн. и 4300 грн.

Определить месячный план производства бензина сортов А и В, который максимизировал бы стоимость выпущенной продукции. Ограничиться составлением математической модели.