Получили решение в виде таблицы
Таблица 6.8
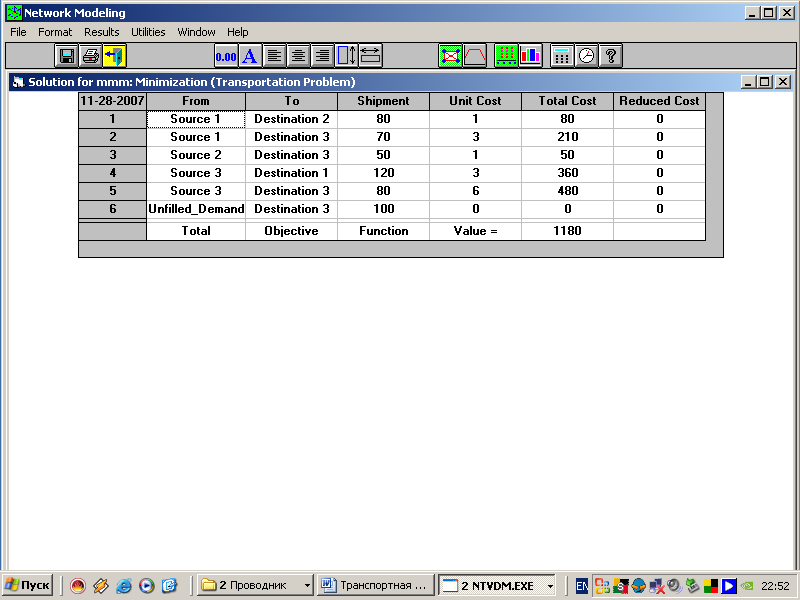
Решение можно получить в виде схемы. Для этого последовательно выполняем действия:
-
11.
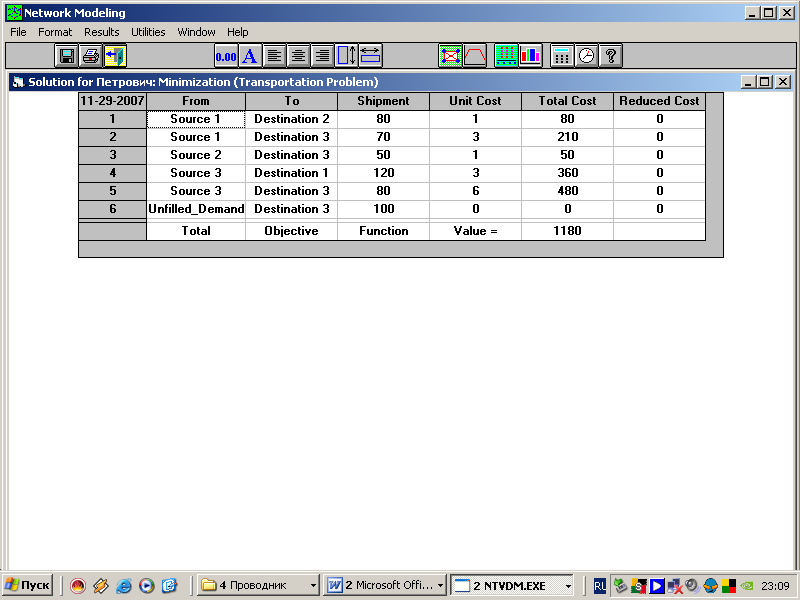
12.
13.
На экране появится решение в виде схемы:
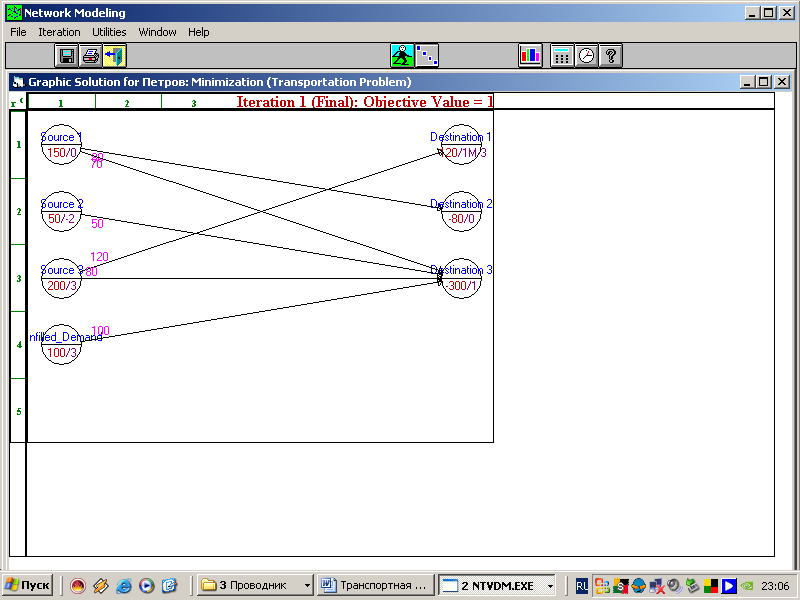
Рис.6.1
В таблице и на схеме выписано оптимальный объем грузов, который необходимо перевозить от каждого поставщика каждому потребителю с указанием стоимости перевозки.
Аналогично оптимальное решение можно получить и с помощью программы QSB.
7. Многофакторные линейные эконометрические модели
Пример 7.1.
Имеются данные о сменной добыче угля
на одного рабочего
(т),
мощности пласта
(м)
и уровне механизации работ
(%),
характеризующие процесс добычи угля в
10 шахтах.
Таблица 7.1.
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
8 |
11 |
12 |
9 |
8 |
8 |
9 |
9 |
8 |
12 |
|
5 |
8 |
8 |
5 |
7 |
8 |
6 |
4 |
5 |
7 |
|
5 |
10 |
10 |
7 |
5 |
6 |
6 |
5 |
6 |
8 |
Предполагая, что между переменными , , существует линейная зависимость, требуется: 1) найти уравнение регрессии по и ; 2) с помощью алгоритма пошаговой регрессии построить эконометрическую модель с максимальным числом значимых коэффициентов при уровне значимости 0,05; 3) построить точечный и интервальный прогнозы для при допущении, что средние показатели по независимым переменным будут превышены на 5%.
Решение. Сформируем матрицы данных:
;
.
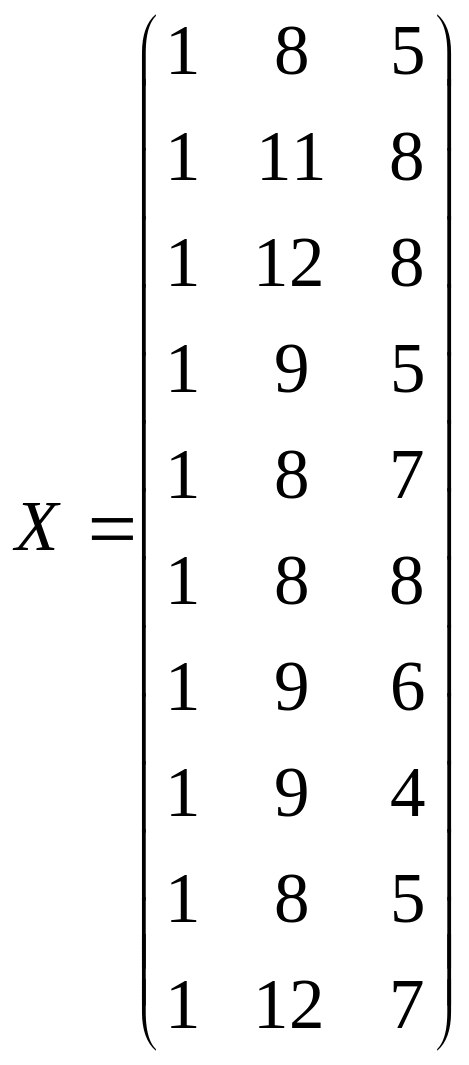Единичный столбец пишется для того, чтобы в уравнении регрессии получить свободный член.
Расчёты проведём в Microsoft Excel, округляя числа до четвёртого знака после запятой. Найдём оператор оценивания 1МНК.
Уравнение линейной регрессии имеет вид
.
(7.1)
Коэффициенты
находятся с помощью действий над
матрицами:
,
(7.2)
Эти
преобразования выполняются в Excel
математическими действиями умножения
матриц и нахождения обратной матрицы:
,
Математические, МУМНОЖ, МОБР. Для
выполнения указанных действий после
ввода данных надо одновременно нажать
клавиши: ↑ , Ctrl, Enter.
Линейное уравнение множественной регрессии имеет вид:
.
Найдём несмещённую оценку дисперсии остатков:
,
(7.3)
,
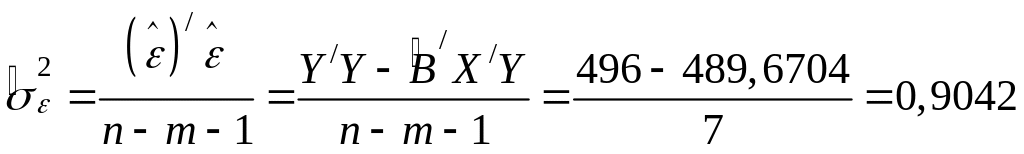(7.4)
где
– число наблюдений,
– количество независимых переменных.
Определим ковариационную матрицу оценок параметров эконометрической модели:
.
(7.5)
Следовательно, квадраты стандартных ошибок равны:
;
;
.
Вычислим общую
дисперсию
результативного
признака и остаточную дисперсию
:
;
.
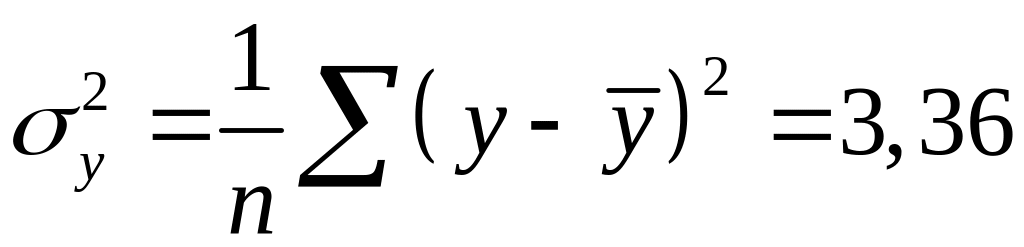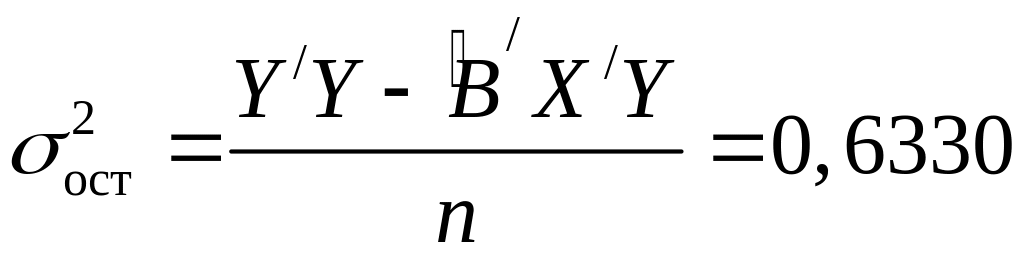(7.6)
Множественный коэффициент детерминации равен:
.
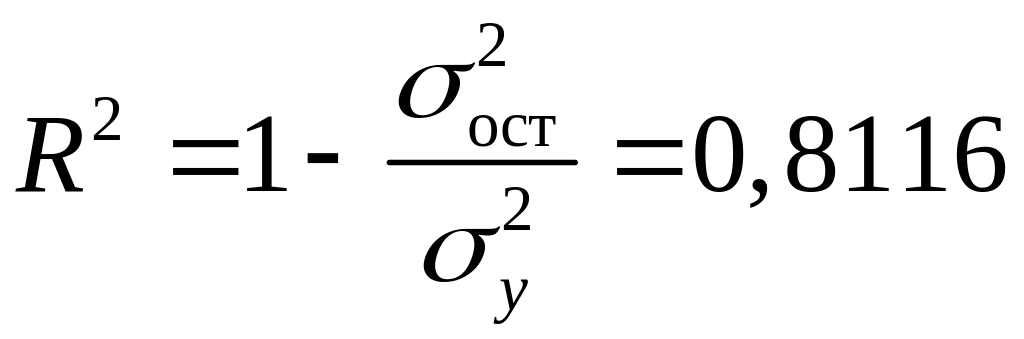(7.7)
Скорректированный множественный коэффициент детерминации:
.
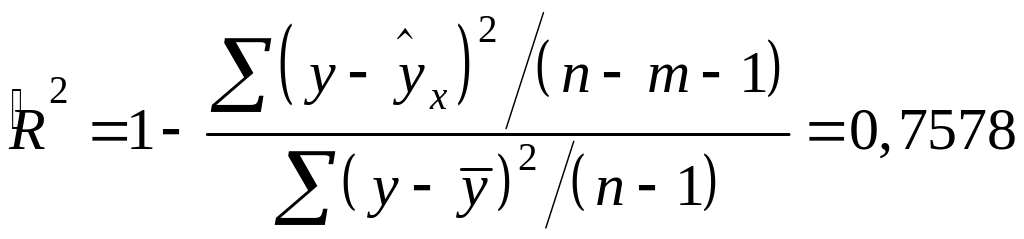(7.8)
Это означает, что дисперсия результативного признака , объясняется на 75,78% влиянием переменных и . Оставшаяся доля дисперсии 24,22% вызвана влиянием других, не учтённых в модели, факторов.
Средняя ошибка аппроксимации составляет:
,
(7.9)
что практически соответствует норме.
Множественный
коэффициент корреляции и его
скорректированное значение, соответственно,
равны:
;
.
Близость к 1 говорит о тесной связи
результативного признака со всем набором
исследуемых факторов.
Рассчитаем
наблюдаемое значение
-критерия
Фишера:
.
(7.10)
Сравним его с
табличным значением при уровне значимости
и степенях свободы
и
:
.
Так как
,
то найденное уравнение регрессии статистически значимо с надёжностью не менее 95%.
Вычислим фактическое
значение
-критерия
Стьюдента:
,
(7.11)
которое сравним
с табличным значением при уровне
значимости
и числе степеней свободы
:
.
Так как
,
то множественный коэффициент корреляции статистически значим с надёжностью не менее 95%.
Для проверки значимости коэффициентов регрессии их величины сравниваются с их стандартными ошибками. Определим фактические значения -критерия Стьюдента:
;
;
,
(7.12)
которые затем сравниваются с табличным значением . Так как
,
,
то оценка коэффициента
регрессии
статистически значима с надёжностью
не менее 95%, а оценка
статистически незначимая.
Следовательно,
независимая переменная
должна быть исключена из модели.
Продолжим выполнение алгоритма пошагового регрессионного анализа.
Для этого повторим
расчёты, описанные в этом разделе для
.
Сформируем матрицы исходных данных:
;
.
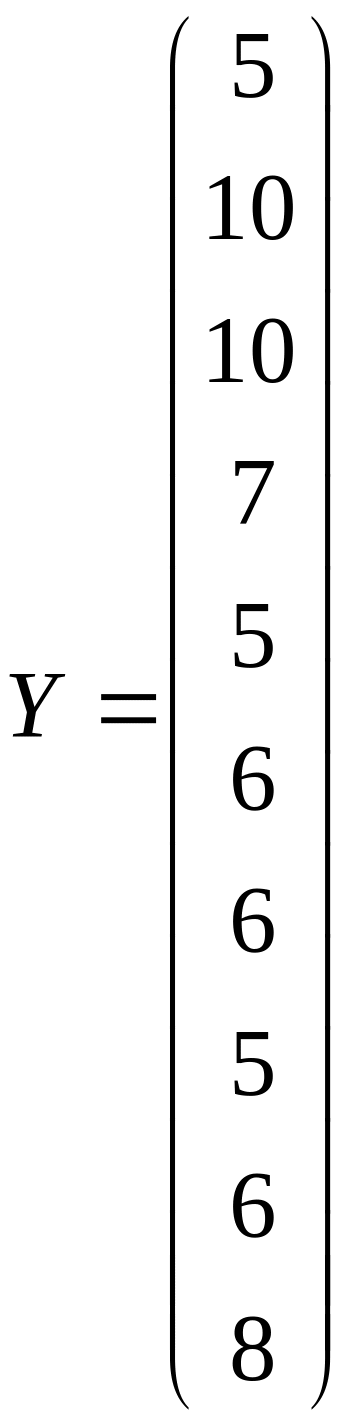Найдём оператор оценивания 1МНК.
,
Новое уравнение регрессии имеет вид:
.
Несмещенная
оценка дисперсии остатков:
.
Ковариационная матрица оценок параметров
эконометрической модели:
.
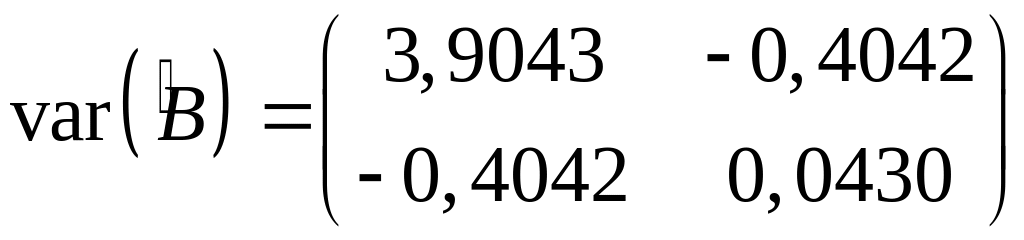Квадраты стандартных
ошибок равны:
;
.
Общая дисперсия
результативного признака и остаточная
дисперсия:
;
.
Множественный коэффициент детерминации:
.
Скорректированный
множественный коэффициент детерминации:
.
Это означает, что дисперсия результативного
признака
,
объясняется на 71,90% (ранее было 75,78%)
влиянием переменной
.
Оставшаяся доля дисперсии 28,10% вызвана
влиянием других, не учтённых в модели,
факторов.
Средняя ошибка
аппроксимации
,
что несколько больше нормы. Множественный
коэффициент корреляции и его
скорректированное значение, соответственно,
равны:
;
.
Близость к 1 говорит о достаточно тесной
связи результативного признака с
фактором
.
Наблюдаемое
значение
-критерия
Фишера:
.
Сравним его с табличным значением при
уровне значимости
и степенях свободы
и
:
.
Так как
,
то найденное уравнение регрессии статистически значимо с надёжностью не менее 95%.
Фактическое
значение
-критерия
Стьюдента
сравним с табличным значением при уровне
значимости
и числе степеней свободы
:
.
Так как
,
то множественный коэффициент корреляции статистически значим с надёжностью не менее 95%.
Проверим значимость
оставшегося коэффициента регрессии
.
Определим фактические значения
-критерия
Стьюдента:
;
.
Так как
,
то оценка коэффициента регрессии статистически значима с надёжностью не менее 95%.
Итак, алгоритм пошагового регрессионного анализа привёл нас к эконометрической модели с максимальным числом значимых коэффициентов регрессии:
.
По соответствующим формулам найдём доверительные интервалы оценок параметров, входящих в модель:
;
;
;
.
3) Построим точечный и интервальный прогнозы для при допущении, что средние показатели по и будут превышены не более чем на 5%.
Так как
,
то предполагаемое значение:
(м).
Вектор предполагаемых значений:
.
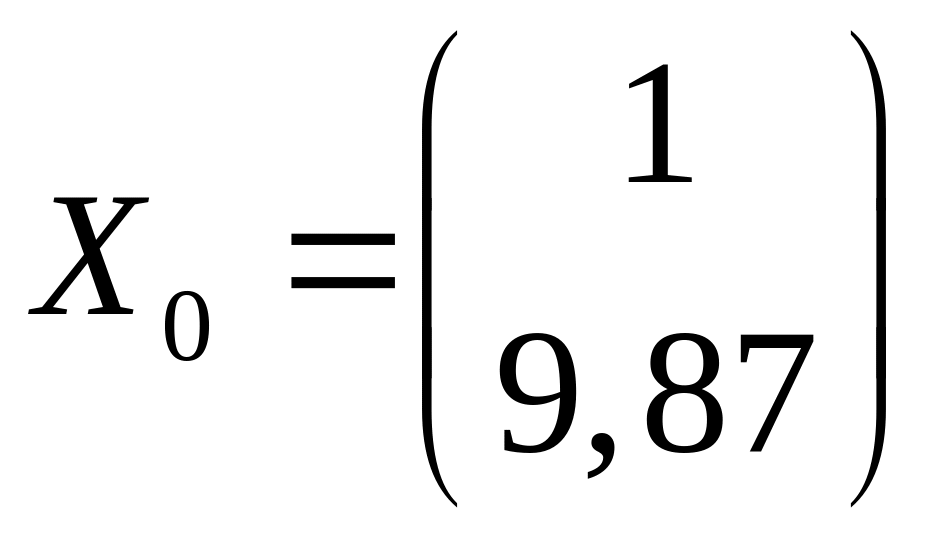Точечный прогноз для среднего значения регрессанта :
(т).
Дисперсия прогноза:
.
Среднеквадратическая
ошибка прогноза:
.
Доверительный интервал для среднего значения (математического ожидания) прогноза зависимой переменной:
;
(7.13)
.
Доверительный интервал для индивидуального значения прогноза:
;
(7.14)
.
где соответствующая стандартная ошибка определяется из формулы:
.
Задача, поставленная в этом разделе, решена.
Замечание. Уравнение регрессии и его анализ легко получить в Excel. Для этого надо последовательно выполнить действия: Сервис, Анализ данных. Для переменных Х выделяют все столбцы данных независимых переменных. Надо указать количество знаков после запятой. Так как таблицы часто не помещаются на странице, то их можно печатать в альбомном виде. Если указать три знака после запятой, то получим решение первой части примера 7.1 в следующем виде.
ВЫВОД ИТОГОВ |
|
|
|||||||||||||||||
|
|
|
|||||||||||||||||
Регрессионная статистика |
|
|
|||||||||||||||||
Множественный R |
0,901 |
|
|||||||||||||||||
R-квадрат |
0,812 |
|
|||||||||||||||||
Нормированный R-квадрат |
0,758 |
|
|||||||||||||||||
Стандартная ошибка |
0,951 |
|
|||||||||||||||||
Наблюдения |
10,000 |
|
|||||||||||||||||
Дисперсионный анализ |
|
||||||||||||||||||
|
df |
SS |
MS |
F |
Значимость F |
|
|||||||||||||
Регрессия |
2,000 |
27,270 |
13,635 |
15,079 |
0,003 |
||||||||||||||
Остаток |
7,000 |
6,330 |
0,904 |
|
|
||||||||||||||
Итого |
9,000 |
33,600 |
|
|
|
||||||||||||||
|
|
||||||||||||||||||
|
Коэф- Фици- енты |
Стандар- тная ошибка |
t- статис- тика |
P-Значе ние |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
|
||||||||||
Y-пересечение |
-3,539 |
1,907 |
-1,856 |
0,106 |
-8,048 |
0,969 |
-8,048 |
0,969 |
|
||||||||||
Переменная X 1 |
0,854 |
0,221 |
3,873 |
0,006 |
0,333 |
1,375 |
0,333 |
1,375 |
|
||||||||||
Переменная X 2 |
0,367 |
0,243 |
1,511 |
0,175 |
-0,207 |
0,942 |
-0,207 |
0,942 |
|
||||||||||