Заполняем новую таблицу.
Таблица 6.6
bj ai |
120 |
80 |
300 |
ui |
|||
150 |
|
4 |
|
1 |
|
3 |
|
[-4] |
|
80 |
|
70 |
|
u1=0 |
|
50 |
|
2 |
|
0 |
|
1 |
|
[-4] |
|
[-1] |
|
50 |
|
u2 = – 2 |
|
200 |
|
3 |
|
5 |
|
6 |
|
120 |
|
[-5] |
|
80 |
|
u3 = – 1 |
|
100 |
|
0 |
|
0 |
|
0 |
|
[-3] |
|
[–2] |
|
100 |
|
u4 = –3 |
|
vj |
v1 = 0 |
v2 = 1 |
v3 = 3 |
|
|||
Получили третий план.
Третий план оптимальный, так как все оценки отрицательные.
В ответе четвертую строку не пишем. Третий потребитель недополучает 100 единиц груза.
Ответ
,
Z
Opt.
=
=
80·1+70·3+50·1+120·3+80·6=1180.
План единственный, так как все оценки свободных клеток строго больше нуля.
Замечание1. Если оценка отрицательна, то не обязательно находить ее значение. Достаточно поставить вместо числа знак «–», то есть отметить, что клетка благоприятная.
Замечание 2. Если задача имеет, например, три опорные оптимальные решения
то общее решение можно записать в виде
где
Замечание 3. При решении транспортной задачи нужно постоянно проверять: 1) баланс, 2) количество заполненных клеток, 3) возможность соединения заполненных клеток соответствующей цепочкой. Тогда арифметические ошибки будут устраняться по ходу решения.
Рассмотрим методику решения транспортной задачи с помощью winqsb.
1. Включить компьютер.
2. Найти и открыть папку WINQSB.
|
|
3. Загружаем файл NET |
4. Активизируем курсором файл |
|
|||
|
5. В появившуюся таблицу вносим данные:
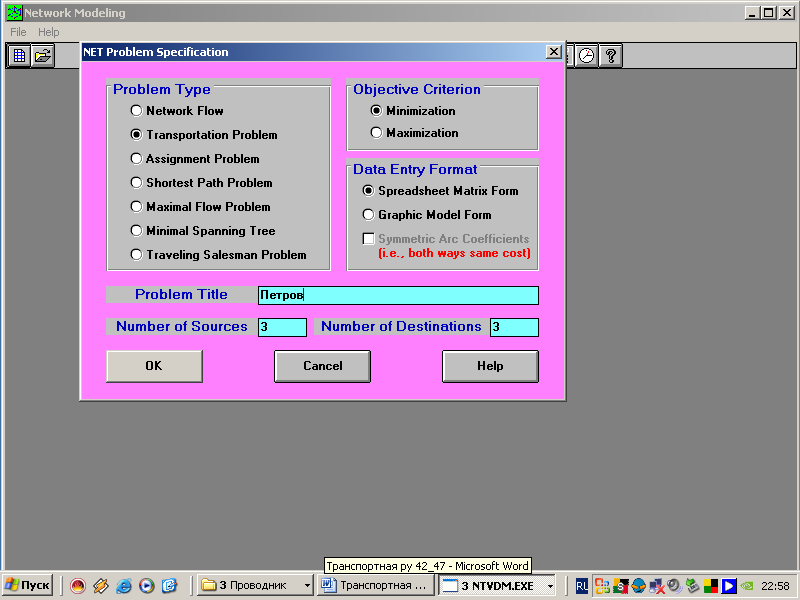
Имя проблемы, например Петров;
Количество поставщиков, в нашем примере 3;
Количество потребителей, в нашем примере 3;
Курсором устанавливаем Minimization, так как наша задача на min;
OK.
6. В появившуюся таблицу вводим числовые коэффициенты задачи:
Таблица 6.7
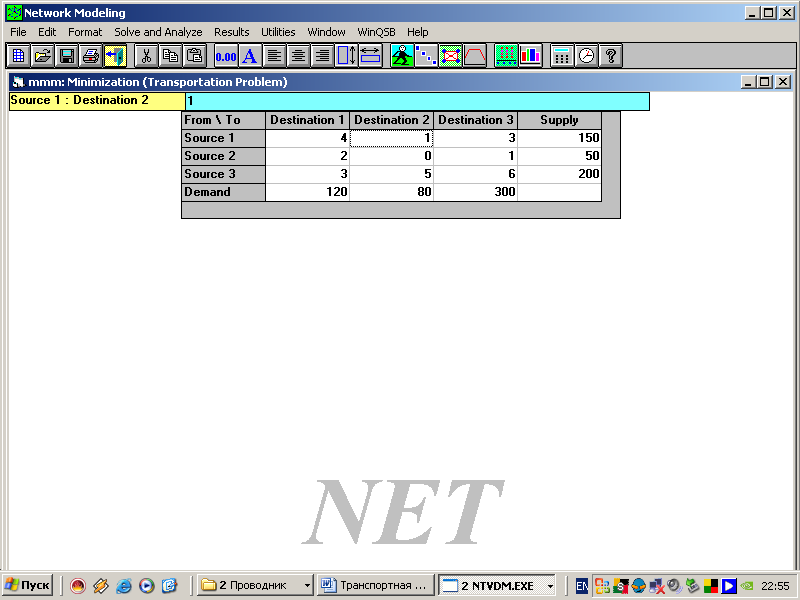
Последовательно выполняем действия.
-
7.
8.
9.