Выпишем алгоритм симплексного метода

1. Задачу приводим к каноническому виду с неотрицательными правыми частями.

2. Находим опорное решение (в каждом уравнении должна быть переменная с коэффициентом единица, которая входит только в одно уравнение).

3. Составляем симплексную таблицу.

Проверяем знаки .

Если все , то оптимальное решение найдено, есть минимум Z.

Если имеются , то составляем новую симплексную таблицу и опять проверяем знаки чисел в индексной строке. Итерации продолжаем до тех пор, пока не получим в индексной строке все неотрицательные числа или установим отсутствие конечного решения задачи ( , а все числа для некоторого j).

Новую симплексную таблицу пересчитываем по правилу полных жордановых исключений.

Замечание 1. Если в оптимальном плане свободный вектор имеет

нулевую оценку и среди чисел есть положительные, то оптимальный план не единственный (может быть вырожденным). Вводя в базис , найдем еще одно оптимальное опорное решение. Если на некотором этапе возникнет столбец с неположительными членами и положительной оценкой для данного столбца, то .

Замечание 2. Если задача на max, то не обязательно переходить к нахождению min. Можно решать задачу на max, но тогда в индексной строке нужно получить неотрицательные оценки. В базис вводят вектор с наименьшей отрицательной оценкой.

Замечание 3. Разрешающий столбец можно выбирать по положительной не наибольшей оценке, иногда это упрощает вычисление и даже уменьшает количество итераций. Например, в базис можно включать вектор, которому соответствует определяется для каждого j.

4. Двойственные задачи линейного программирования. Экономико-математический анализ задачи линейного программирования Сформулируем правило составление двойственных задач

Если задача на max, то ограничение вида «  » будем называть согласованным или правильным, а « » – неправильным, несогласованным. Если задача на min, то ограничение «  » – правильное, а «  » – неправильное.

Прежде, чем сформулировать общее правило составления двойственных задач, рассмотрим пример.

Пример 4.1. Написать двойственную задачу к заданной задаче.

Исходная задача Двойственная задача

Люб. знака

Люб. знака

Из этого примера видно, что двойственная задача к двойственной есть исходная задача. Это можно использовать для проверки правильности составления двойственных задач.

Правило составление двойственных задач

1. Количество двойственных переменных равно количеству ограничений исходной задачи (каждому ограничению ставится в соответствие двойственная переменная).

2. Целевая функция двойственной задачи имеет вид F = b₁y₁+ b₂y₂+…+ b_my_m.

3. Если Z  max, то F  min; если Z  min, то F  max (направление цели F противоположно направлению цели Z).

4. Количество ограничений двойственной задачи равно количеству переменных исходной задачи.

5. Левая часть j-го ограничения двойственной задачи равна , а правая с_j. Если , то j-ое ограничение в двойственной задаче правильное. Если , то j-ое ограничение – неправильное, если имеет любой знак, то j-ое ограничение – « = ».

6. Если i-ое ограничение исходной задачи правильное, то , если i-ое ограничение исходной задачи неправильно, то , если i-ое ограничение исходной задачи « = », то – имеет любой знак.

Матрицы исходной и двойственной задач взаимно транспонированные.

Исходная задача. Двойственная задача.

(4.1)

Знаки ограничений пишут согласно пункту 5, а условия на знак переменных – по пункту 6. Проверка осуществляется по правилу: задача двойственная к двойственной задаче есть исходная задача.

Решение двойственной задачи можно получить, исследуя решение прямой задачи на основании первой и второй теорем двойственности.

По первой теореме двойственности:

1) или , если оптимальное значения целевых функций существуют;

2) Если целевая функция одной из взаимно двойственных задач неограниченная, то двойственная задача имеет несовместную систему ограничений;

3) если система ограничений одной из двойственных задач несовместная, то целевая функция двойственной задачи неограниченна или её система ограничений несовместная.

Оптимальные значения переменных двойственной задачи можно определять по индексной строке последней симплексной таблицы, если в каждом ограничении прямой задачи имеется базисная переменная – переменная, которая входит только в одно уравнение с коэффициентом равным единице или -1.

Чтобы найти надо:

1) в первой строке первой симплексной таблицы выбрать столбец, в котором находится базисная переменная;

2) в этом столбце взять число, которое находится в индексной строке последней симплексной таблицы;

3) к этому числу прибавить коэффициент целевой функции из этого столбца. Это будет .

Аналогично находятся , и т. д.

Пример 4.3. Провести экономико-математический анализ задачи из примера 3.1.

Математическая модель исходной задачи:

(4.2)

Двойственная задача:

(4.3)

Решение двойственной задачи можно найти по индексной строке последней симплексной таблицы.

.

Знак «-» ставится при нахождении потому, что целевая функция умножалась на -1. Поэтому при составлении и решении ЗЛП желательно не менять знаки в целевой функции и ограничениях.

Чтобы проводить анализ решения, задачу надо решать с помощью компьютера.

Изложим методику решение прямой и двойственной задачи с помощью программы WINQSB.

1. Включить компьютер.

2. Найти и открыть папку WINQSB.		3. Загружаем файл LP-I LP (Линейное программирование)	4. Активизируем курсором файл

5. В появившуюся таблицу вносим данные:

• Имя проблемы, например Петров;

• Число переменных, в нашем примере 2;

• Количество ограничений, в нашем примере 3;

• Курсором устанавливаем Maximization, так как наша задача на max;

• OK.

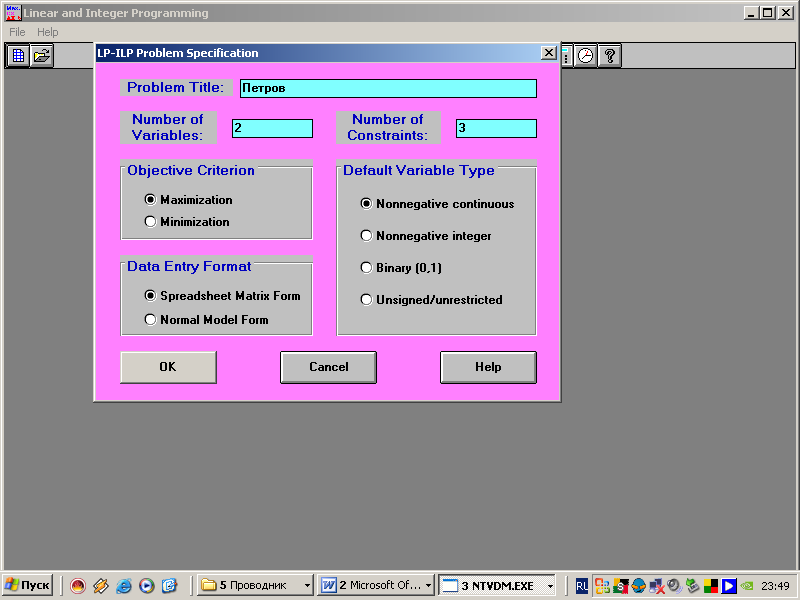
В появившуюся таблицу вводим числовые коэффициенты задачи.

Таблица 4.1

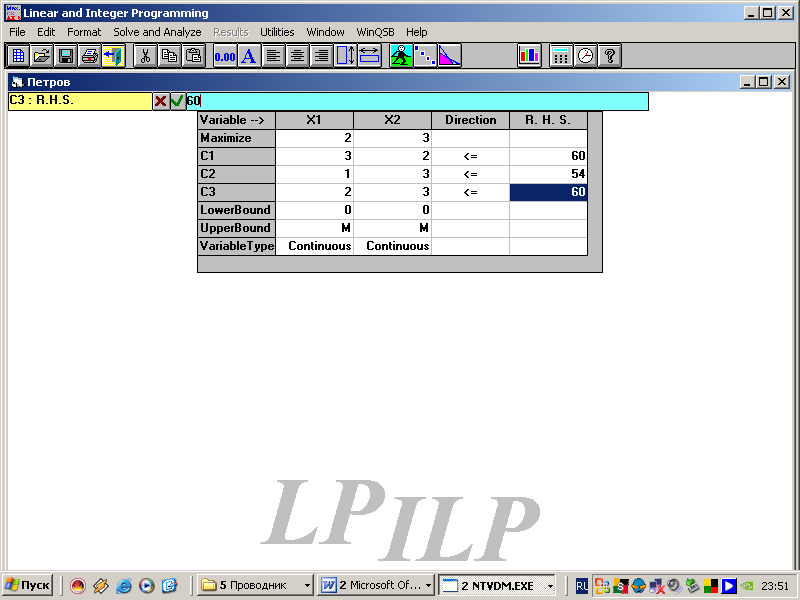
Последовательно выполняем действия.

7.

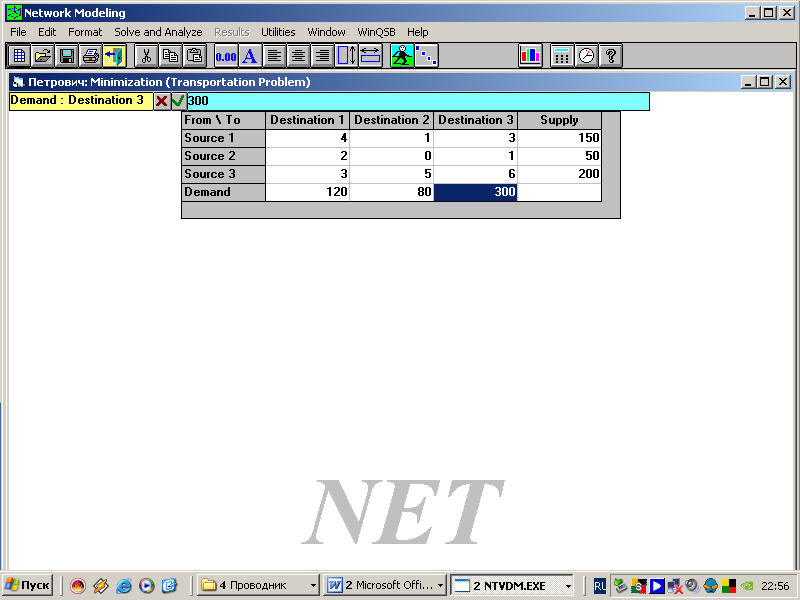
8.

9.

10. Получили решение в виде таблицы

Таблица 4.2

Приведём перевод названий столбцов: Decision variable – переменные, Solution Value – значения переменных, Unit Cost or Profit c[j] – коэффициенты целевой функции, Total Contribution – доход от каждой продукции, Reduced Cost – понижающая оценка, Basis Status – базисная или свободная переменная, Allowable Min. c[j] – минимум коэффициентов целевой функции, Allowable Max. c[j] – максимум коэффициентов целевой функции, Constraint – ограничения, Left Hand Side – количество использованного сырья, Direction – знак ограничения, Right Hand Side – свободные члены ограничений, Slack or Surplus – остаток ресурсов, Shadow Price – теневые цены, Allowable Min. RHS – минимум ресурсов, Allowable Max. RHS – максимум ресурсов. Эти переводы можно увидеть ниже в таблице QSB⁺, а их смысл объясняется в следующих пунктах.

1. Выписываем решение прямой задачи из столбцов Decision variable, Solution Value: , . При этом 12 грн. выручка от реализации первой продукции, 48 грн. – от второй продукции указаны в столбце Total Contribution.

2. Интервалы устойчивости цены единицы продукции находятся в столбцах Allowable Min. c[j] Allowable Max. c[j]:

.

При таких изменениях каждой цены в отдельности оптимальный план выпуска продукции не изменится.

3. По первой теореме двойственности . Это означает, что в пределе затраты на ресурсы равняются выручке от реализованной продукции.

4. Из столбца теневой цены Shadow Price выписываем оптимальное решение двойственной задачи . Теневые цены показывают, что первый и второй ресурсы не дефицитные, могли быть использованы не полностью. Третий ресурс является дефицитным, используется полностью и приобретения его единицы приведёт к увеличению прибыли на грн. или предприятие может заплатить за дополнительную единицу третьего ресурса 1грн.

5. Интервалы устойчивости ресурсов находятся в столбцах Allowable Min. RHS Allowable Max. RHS:

первый ресурс ,

второй ресурс ,

третий ресурс .

Эти интервалы показывают, что при изменении объемов ресурсов, каждого в отдельности, в полученных интервалах, структура оптимального плана не изменится.

Из таблицы видно, что первого ресурса остаётся 10 единиц, а второго и третьего не остаётся. Это показано в столбцах Slack or Surplus и Left Hand Side.

Целесообразность производства продукции по цене и затратами сырья соответственно определяется знаком выражения

. (4.4)

Если , то -ю продукцию целесообразно производить, – нецелесообразно.

Если включить в производство единицу дополнительного (третьего) продукта с затратами сырья 3, 1, 2 на единицу продукции соответственно, со стоимостью 4грн., то разность между прибылью и затратами будет равна

=

Следовательно, новый продукт целесообразно включать в план.

В столбце Reduced Cost выписаны снижающие оценки . Снижающая оценка для небазисной переменной x_j в задаче на max, показывает минимальное значение, на которое может быть увеличен коэффициент с_j, при котором текущий базис перестает быть оптимальным (изменение ассортимента продукции, которая производится). Снижающую оценку еще называют альтернативной ценой. Она представляет собой наибольший ущерб, который может быть получен при принятии решения отличного от оптимального. Она показывает, на сколько ухудшится (уменьшится) значение целевой функции, если соответствующая переменная будет введена в базис. Каждая j-ая единица продукции с ненулевой понижающей оценкой, которую начнут производить, снизит прибыль на . Об этом говорилось в критерии оптимальности.

В столбце Unit Cost or Profit c[j] указаны коэффициенты целевой функции.

В столбцах Constraint, Right Hand Side указаны ограничения и правые части ограничений.

Если работать со старой программой QSB, которая помещается на дискете, то получаем тоже, но с некоторыми изменениями действий и сложностью печатания. можно копировать экран.

Укажем краткую методику пользования этой программой.

1. Найти и открыть папку QSB.

2. Загружаем файл

3. Работаем в диалоговом режиме.

4. Вводим данные задачи.

5. Работаем в диалоговом режиме.

6. В появившуюся таблицу вводим числовые коэффициенты задачи.

Таблица 4.3

7. Решение задачи. В диалоговом режиме выбираем табличный способ решения, можно графическое решение. В последнем случае получим чертёж, который можно срисовать, распечатать, скопировать экран

8. Решить и вывести последнюю таблицу (можно выводить все таблицы).

Таблица 4.4

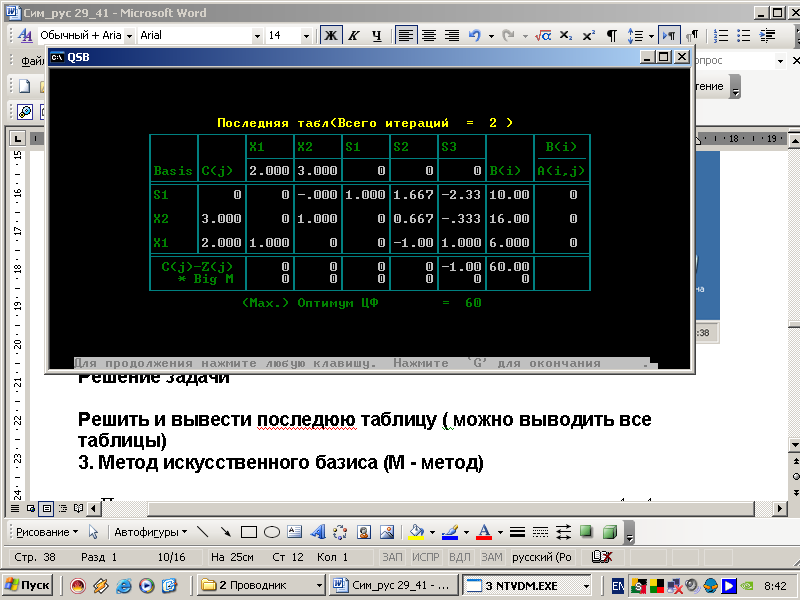
7. Вывести заключительный отчёт.

Таблица 4.5

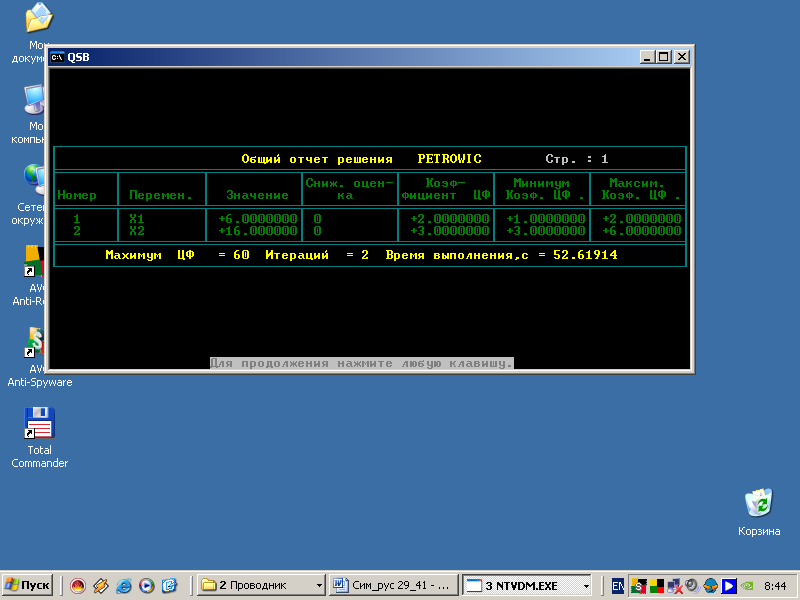
Таблица 3.13

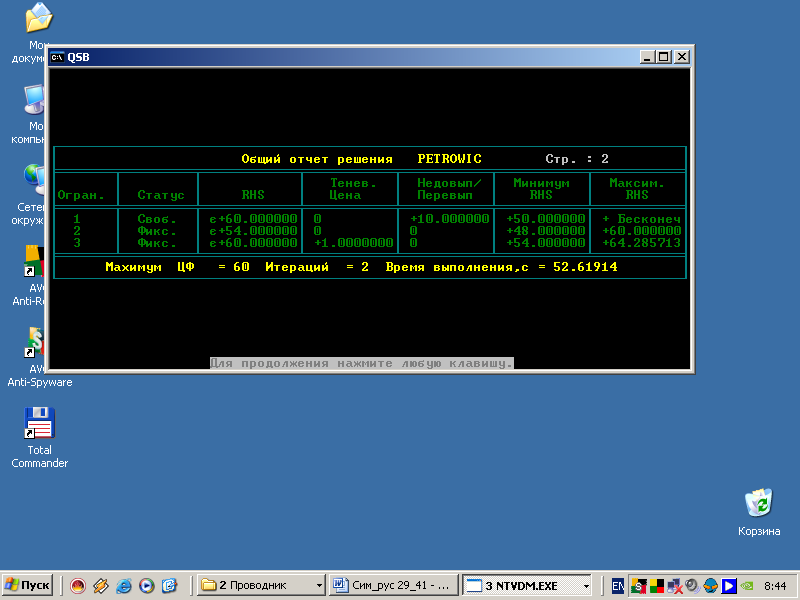
8. Из этих двух таблиц выписываем решение и делаем его анализ.