Тема 6 Правила Кирхгофа

Для разветвленных цепей имеют место два закона Кирхгофа:

первый закон Кирхгофа - алгебраическая сумма токов, сходящихся в узле, равна нулю:

второй закон Кирхгофа - в любом замкнутом контуре алгебраическая сумма падений потенциала на отдельных участках цепи равна алгебраической сумме э.д.с., встречающихся в этом контуре:

При применении законов Кирхгофа надо руководствоваться следующими правилами:

на схеме произвольно указываются стрелками направления токов у соответствующих сопротивлений. Обходя контур в произвольном направлении, будем считать положительными те токи, направления которых совпадают с направлением обхода, и отрицательными те направления которых противоположны направлению обхода.

Положительными э.д.с. будем считать те э.д.с., которые повышают потенциал в направлении обхода, т.е. э.д.с. будет положительной, если при обходе придется идти от минуса к плюсу внутри генератора.

Напомним

+ -

В результате решения составленных уравнений определяемые величины могут получиться отрицательными. Отрицательное значение тока указывает на то, что фактическое направление тока на данном участке цепи обратно принятому.

Задача 52

Найти токи I_i в отдельных ветвях мостика Уинстона при условии, что через гальванометр идет ток I_r=0 . Э.д.с. элемента Е=2,2 В. Сопротивления резисторов R_i=30 0м, R₂=45 0м и R₃=200 0м.

Дано: Е=2,2 В R1=30 0м R2=45 0м R3=200 0м Ir=0	Решение: Обозначим направление токов, выберем направление обхода всех контуров по часовой стрелки. По первому закону Кирхгофа составим уравнения для узла В и D, пользуясь условием, говорящем о том, что Ir=0:
I1, I2, I3, I4 – ?	узел В:

I₁ - I₂ = 0  I₁ = I₂ (1)

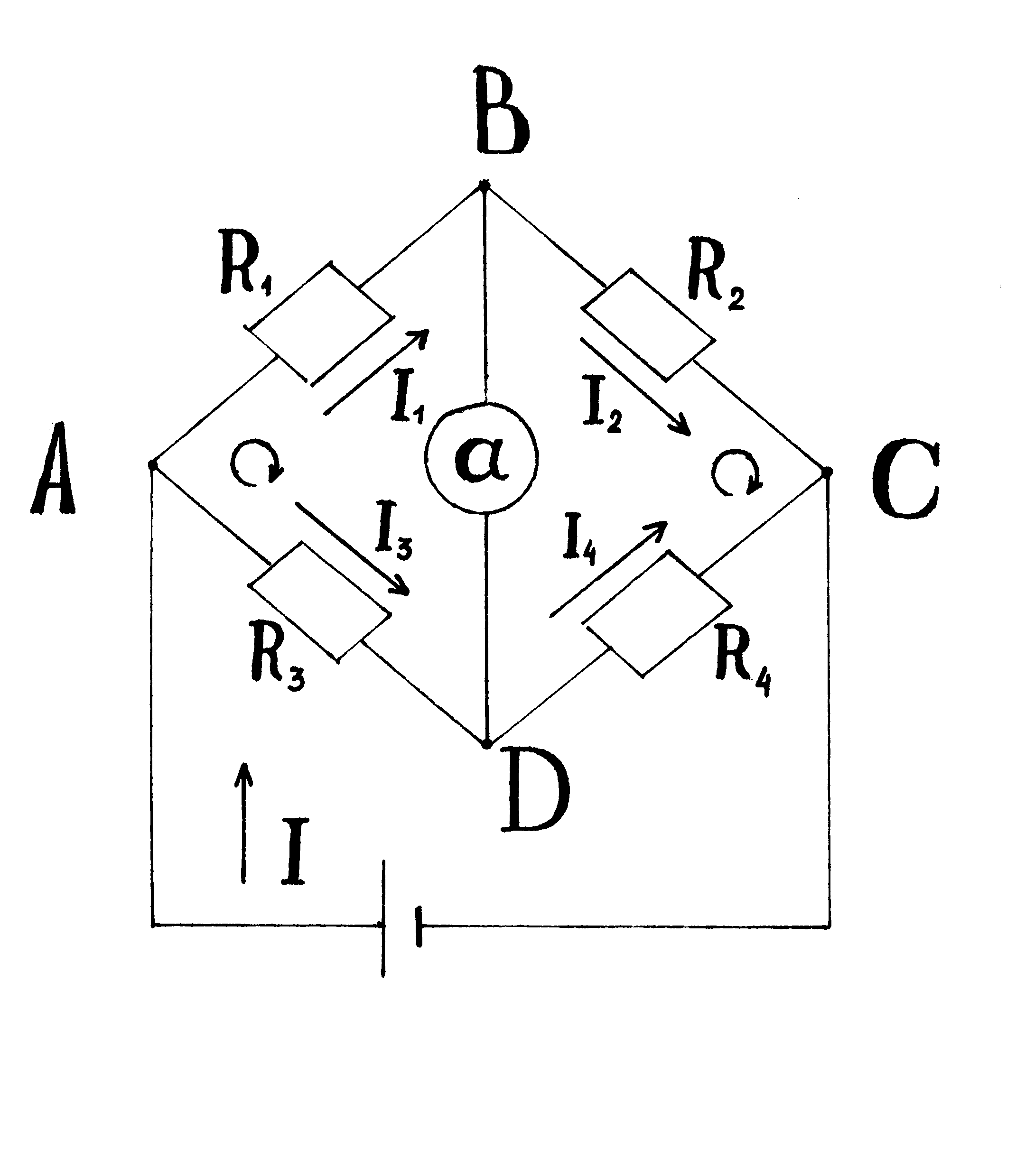
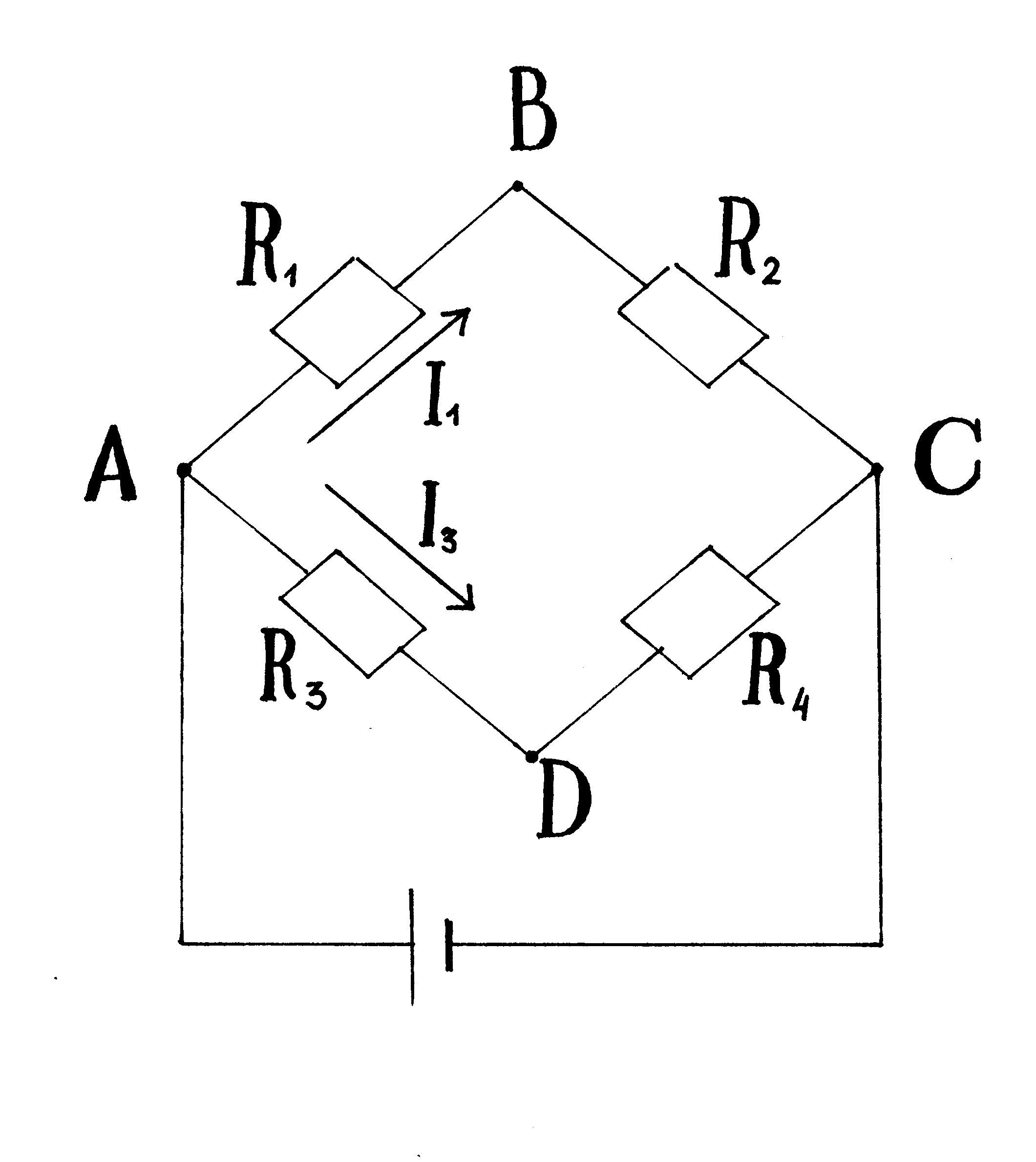
узел D:

I₃-I₄=0  I₃ = I₄ (2)

По второму правилу Кирхгофа составим уравнения для контуров BСDВ и АВDА.

Контур BСDВ:

I₂R₂ – I₄R₄ = 0 (2)

Данное выражение получилось таким из условия, что

r = 0 (3)

Контур АВDА:

I₁R₁ - I₃R₃=0 (4)

Контур АВСEFА:

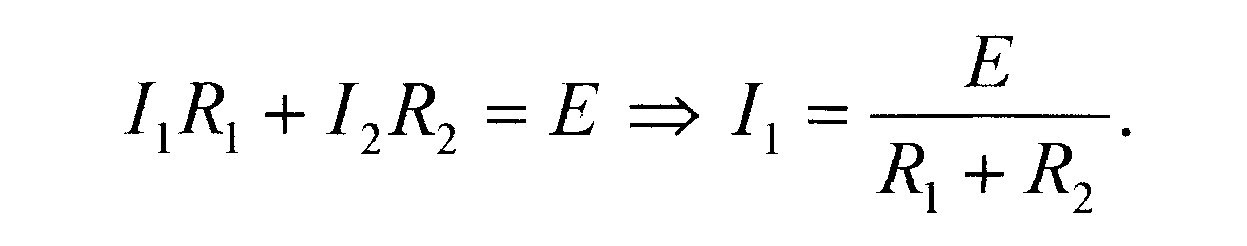(5)

Преобразуем выражение (4) и подставим формулу (5), получаем

I₁R₁ = I₃R₃

= I₃R₃  =

Вычисления:

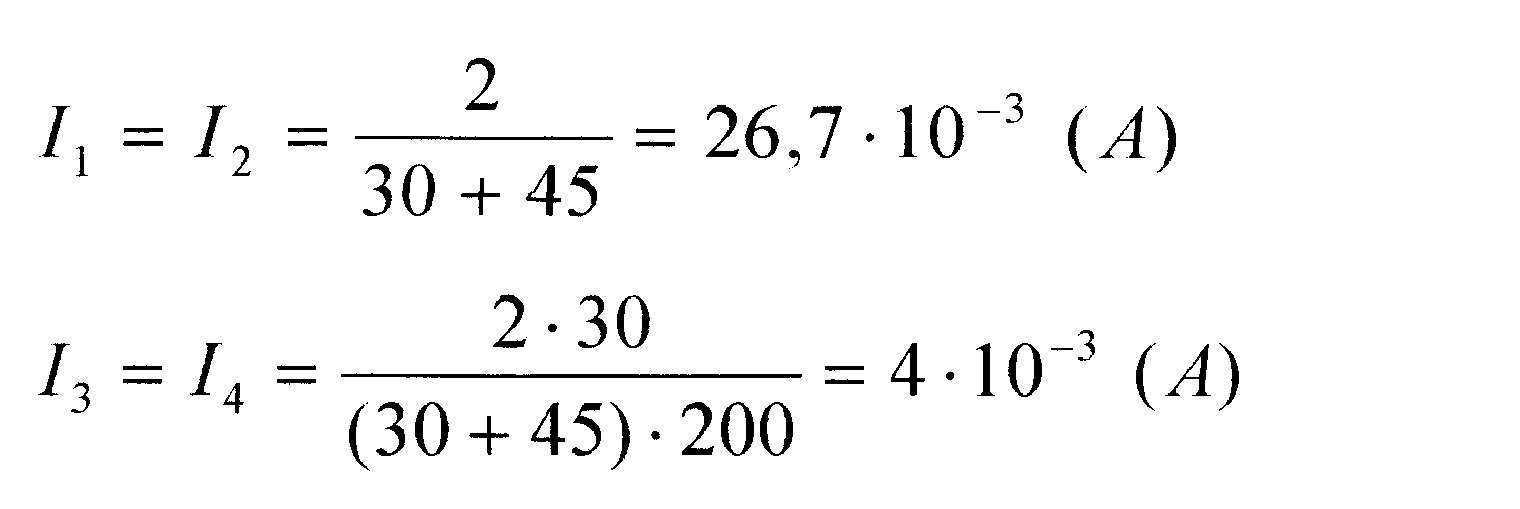
Ответ: токи в ветвях с сопротивлениями R₁ и R₂ равны I₁=I₂=26,7·l0^-3 А, токи в ветвях с сопротивлениями R₃ и R₄ равны I₃=I₄=4·l0^-3 А.

Задача 53

Э.д.с. элементов E₁=2,l В и E₂=l,9 В, сопротивления R₁=45 0м, R₂=10 0м и R₃=10 0м. Найти токи I_i во всех участках цепи.

Дано: E1=2,l В Е2=1,9 В R1=45 0м R2=10 0м R3=10 0м	Решение: Обозначим направление токов как показано на рисунке. Направление обхода контура показано на рисунке. По первому правилу Кирхгофа составим уравнение для узла С: -I1 + I3 + I2 = 0  I1 = I2 + I3
I1, I2, I3 – ?

A E₁ B

R₁

I₁ I₃

E₂ R₂ R₃

D I₂ C

По второму правилу Кирхгофа составим уравнения для контуров АВСА и ACDA:

контур АВСА: I₃R₃+I₁R₁ = E₁,

контур ACDA: I₁R₁+I₂R₂ = E₂.

Из полученных выражений составим систему уравнений:

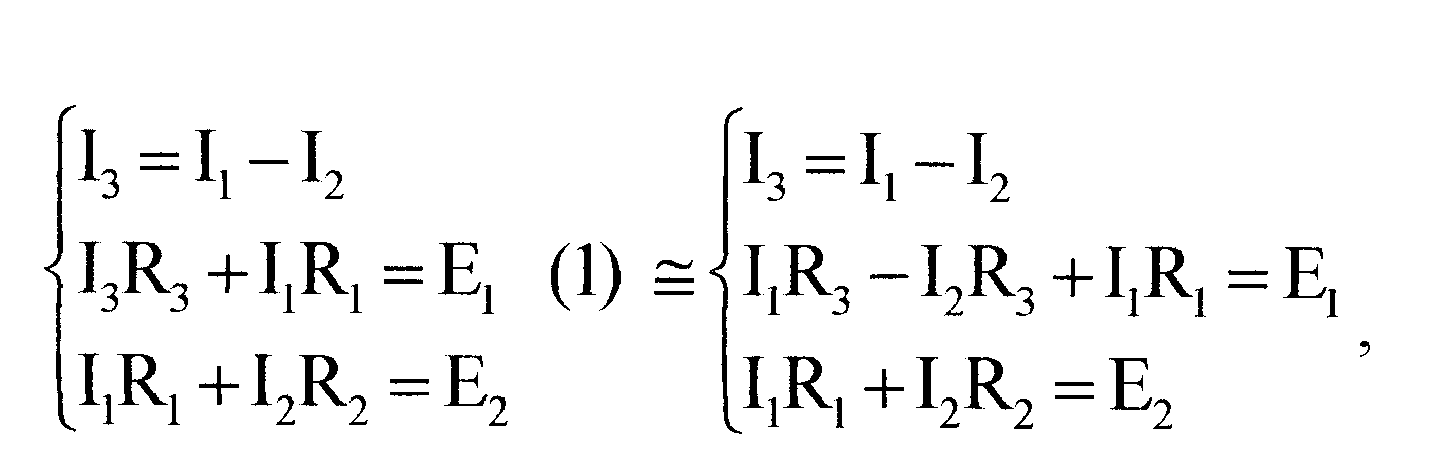
отсюда

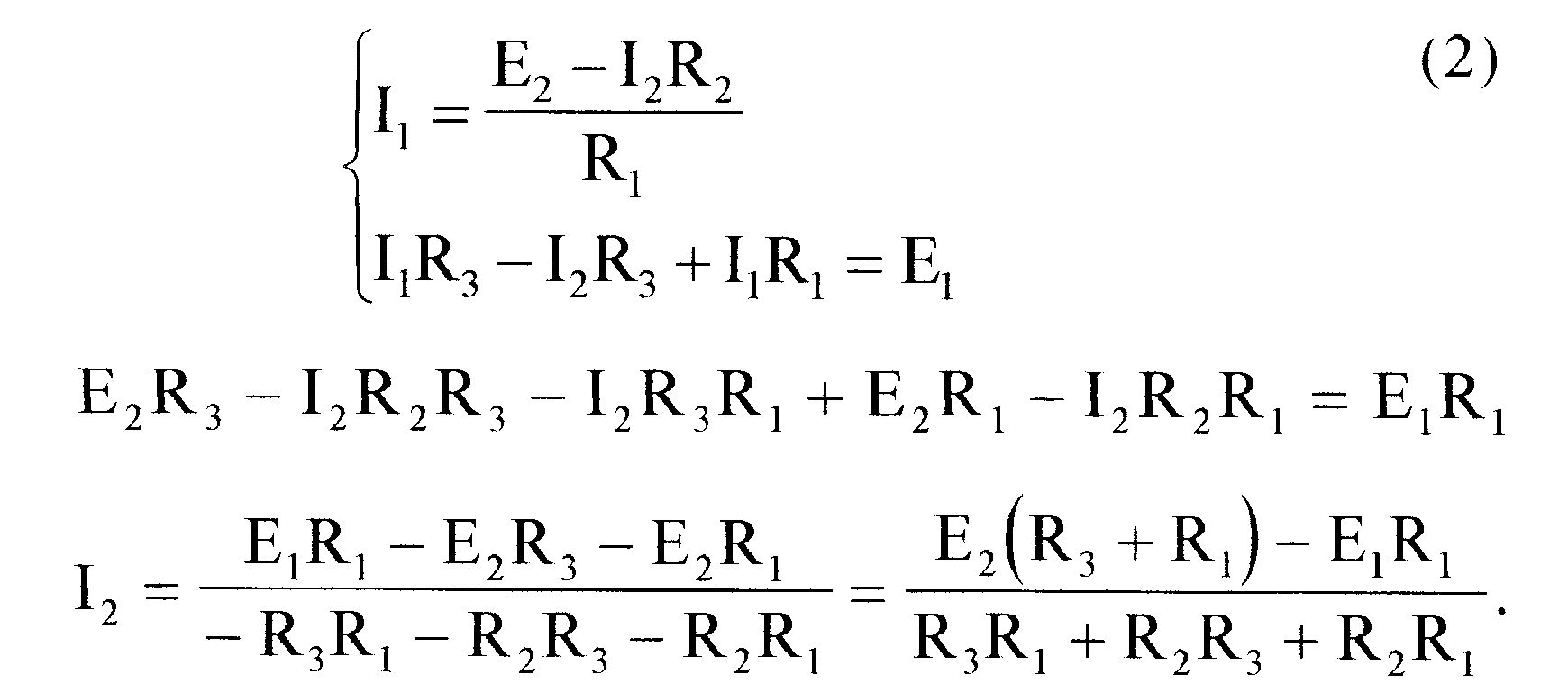
Подставим полученное выражение в (1), получаем:

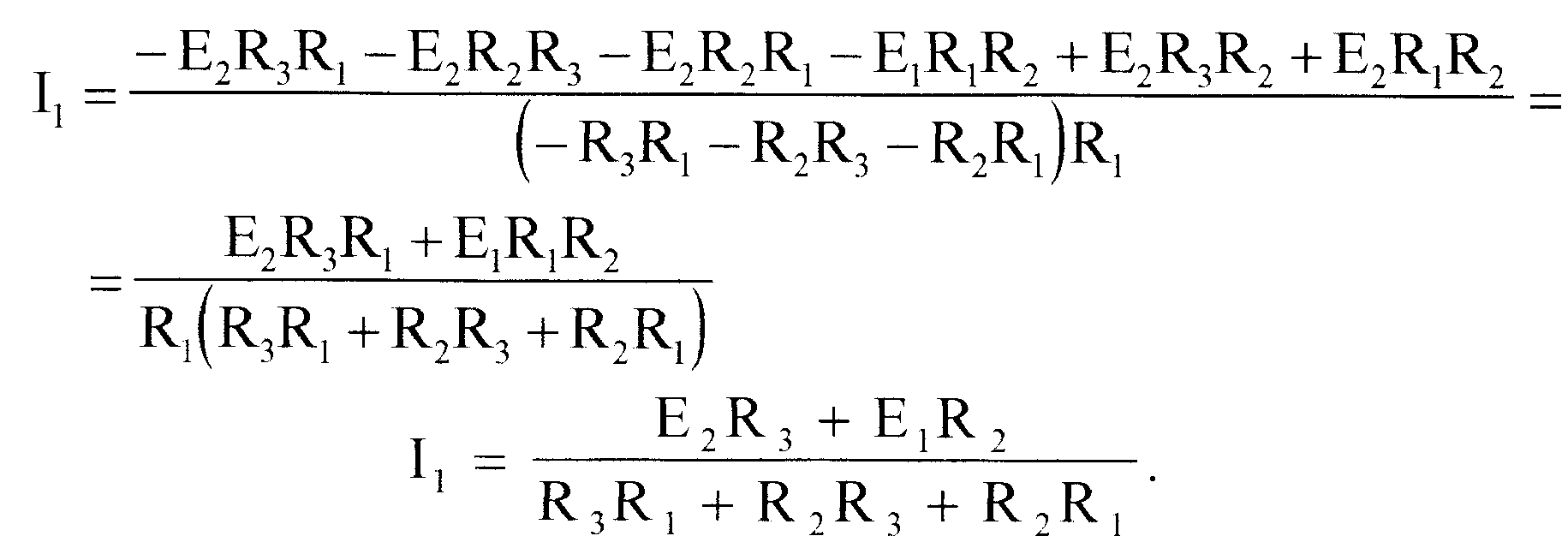
Ток, текущий в ветви с сопротивлением R₃, найдем из формулы (2), как

I₃ = I₁ - I₂.

Вычисления:

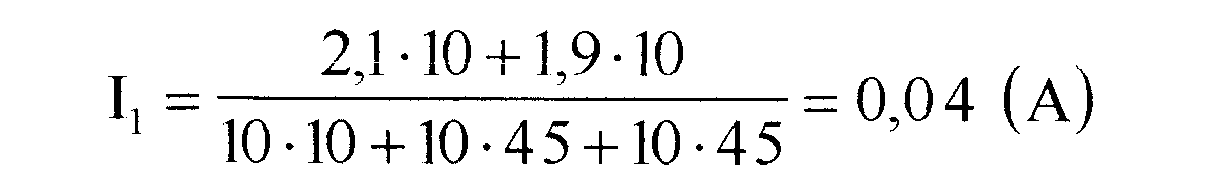
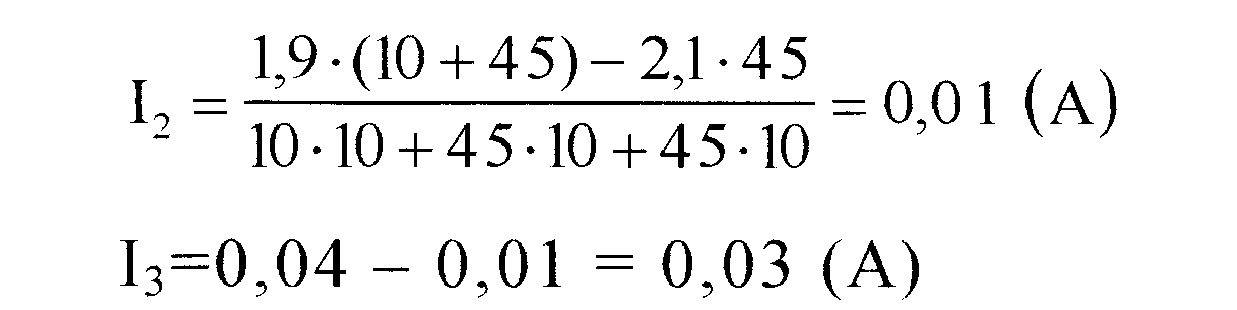
Ответ: токи в участках цепи с сопротивлениями R₁, R₂, R₃ соответственно равны I₁=0,04 А, I₂=0,01 А, I₃=0,03 А.