Задача 87

Найти отношение q/m для заряженной частицы, если она, влетая в однородное магнитное поле с напряженностью Н=200 кА/м со скоростью движется по дуге окружности радиусом R=8,3 см. Направление движения частицы перпендикулярно к направлению магнитного поля. Сравнить значение со значением q/m для электрона, протона и альфа частицы.

Дано: Н=200 кА/м R=8,3 см  = 90° 0 = 12,56·10-7 Гн/м	Решение: На частицу действует сила, всегда перпендикулярная к скорости движения частицы. Это значит, что работа силы всегда равна нулю, следовательно, абсолютное значение скорости движения частицы, а значит, и
q/m - ?	энергия частицы остаются постоянными

при движении. Т.к. =const, то

F = qB. (1)

Эта сила, будучи перпендикулярной направлению движения является центростремительной силой.

При этих условиях заряженная частица движется равномерно по окружности. При этом

Как известно, по второму закону Ньютона величина F=ma или в нашем случае

(2)

Приравняв выражения (1) и (2), получаем

(3)

Магнитная индукция В связана с напряженностью Н магнитного поля соотношением

(4)

Подставляя (4) в (3), получаем

Вычисления:

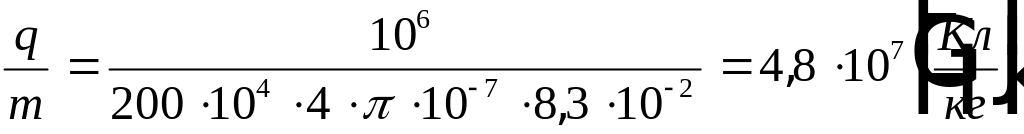
Сравнивая полученное значение отношения с предложенными в условии задачи

1. для электрона ,

2. для протона ,

3. для альфа частицы .

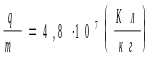мы приходим к выводу, что неизвестной заряженной частицей является альфа частица.

Ответ: отношение для альфа частицы составляет

Задача 88

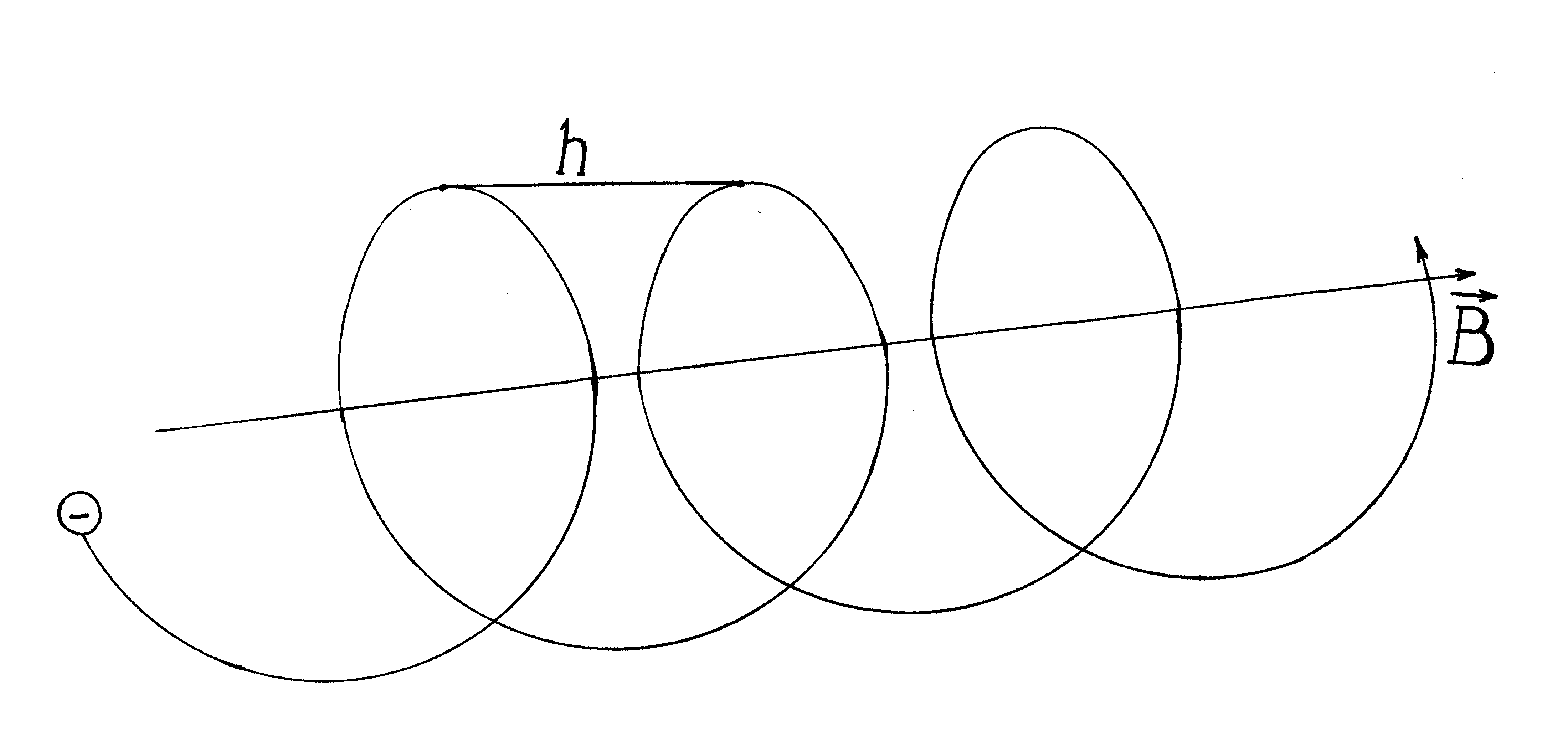
Электрон, ускоренный разностью потенциалов U=6 кВ, влетает в однородное магнитное поле под углом 30 градусов к направлению поля и движется по винтовой траектории. Индукция магнитного поля В=13 мТл. Найти радиус R и шаг h винтовой траектории.

Дано: U=6 кВ В=13 мТл  = 30°	Решение: Если ускоряющее поле совершает над частицей работу A=eU, то частица приобретает кинетическую энергию .
R, h - ?	Согласно закону сохранения и превраще-

ния энергии

. (1)

В этом случае удобно разложить скорость ₀ на две составляющие, одна из которых =₀ cos  параллельна полю, а другая _n = ₀ sin перпендикулярна к полю.

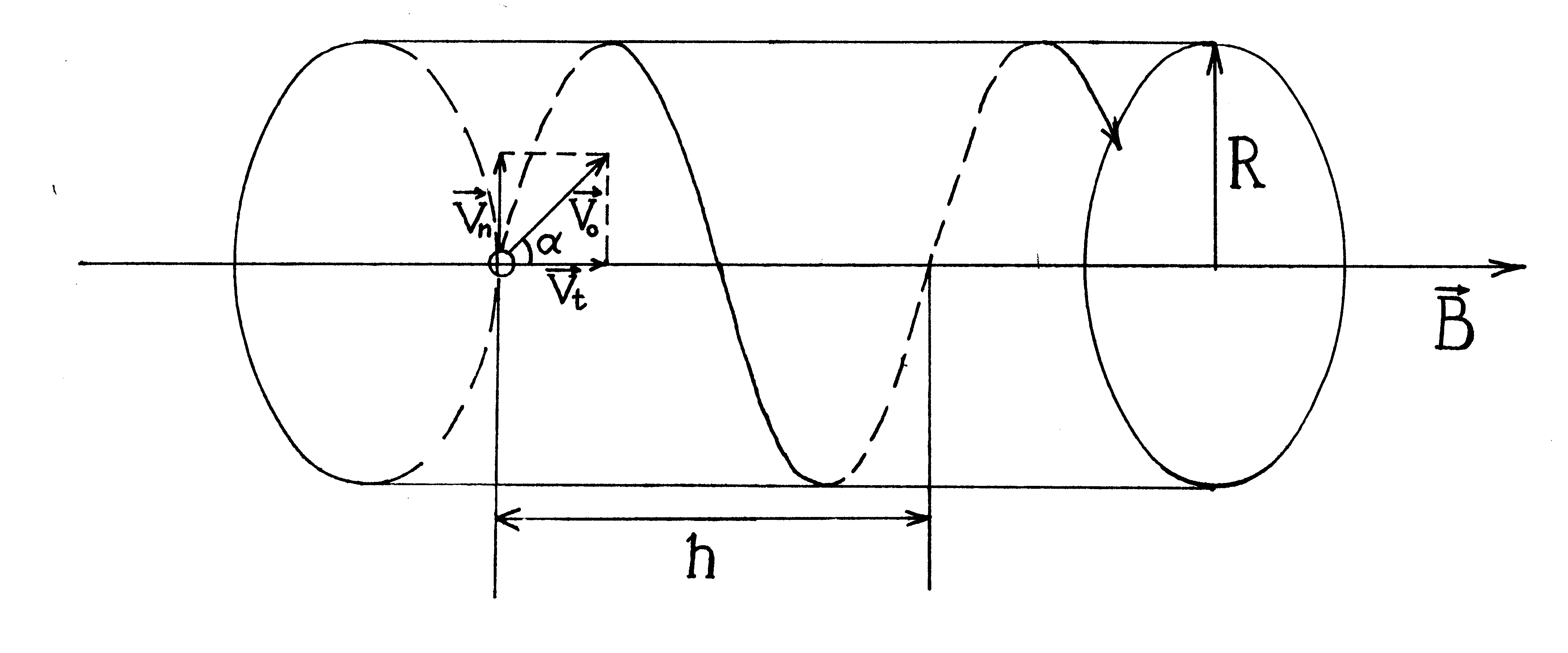
На частицу действует сила Лоренца, обусловленная составляющей _n и частица движется по окружности, лежащей в плоскости, перпендикулярной к полю.

Составляющая _ не вызывает появления добавочной силы, т.к. сила Лоренца при движении параллельно полю равна нулю. Поэтому в направлении поля частица движется равномерно со скоростью  = ₀ cos.

В результате сложения обоих движений частица будет двигаться по цилиндрической спирали.

Проекция траектории электрона на плоскость, перпендикулярную индукции В, представляет собой окружность, радиус которой равен искомому радиусу винтовой траектории и определяется формулой, выведенной из ранее полученного соотношения двух выражений для силы Лоренца

. (2)

Подставляем (1) в (2), получаем

. (3)

или

.

Период обращения электрона

. (4)

Подставим (3) в (4), получаем:

.

Шаг винтовой траектории электрона:

.

Вычисления:

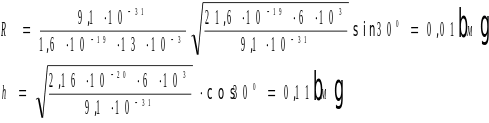
Ответ: радиус винтовой траектории, образованный при движении электрона, равен R=0,01 м, шаг винтовой траектории h=0,11 м.