Задачи по физике. Электричество и магнетизм. Часть I

Тема 5

Работа и мощность электрического тока

Работа электрического тока на участке цепи определяется формулой

Для замкнутой цепи закон Ома имеет вид

где Е – э.д.с. генератора,

R – внешнее сопротивление,

r – внутреннее сопротивление генератора.

Полная мощность, выделяемая в цепи

Задача 43

Имеются три 110-вольтовых электрических лампочки, мощности которых равны Р₁=Р₂=40 Вт и Р₃=80 Вт. Как надо включить эти лампочки, чтобы они давали нормальный накал при напряжении сети U=220 В? Начертить схему. Найти токи I₁, I₂, I₃, текущие через эти лампочки, при нормальном накале.

Дано: Р1=Р2=40 Вт Р3=80 Вт U0=220 B U=110 B	Решение: Сопротивление лампочек определим по формуле (1)
I1, I2, I3 – ?	Общее сопротивление двух параллельно соединен

ных лампочек с учетом того, что

Р₃=2Р₂,

E

Л1

Л3

Л2

будет равно

и R_экв=R₃.

Отсюда напряжение в цепи будет:

IR₃+Ir_экв=U₀.

I=const, т.к. соединение последовательное.

2U=U₀

напряжение на лампочках.

По закону Ома для участка цепи ток на лампочке I₃ будет равен

Перепишем данное выражение с использованием формулы (1)

Ток на лампочках Л1 и Л2, будет равным, т.к.

U₁=U₂ и R₁=R₂,

т.е. с использованием формулы (1) получаем, что

Вычисления:

Ответ: для нормального накала нити лампочки с предложенными эксплуатационными условиями токи на лампочках Л1, Л2, Л3 соответственно равны I₁=I₂=0,365 A, I₃=0,73 A.

Задача 44

В лаборатории, удаленной от генератора на расстояние l = 100 м, включили электрический нагревательный прибор, потребляющий ток I=10 A. На сколько понизилось напряжение U на зажимах электрической лампочки, горящей в этой лаборатории, если сечение медных проводящих проводов S=5 мм²?

Дано: l=100 м I=10A S=5 мм2	Решение: Общая длина проводов в цепи равна 2l. Сопротивление проводов найдем из формулы (1)
U – ?

На схеме в цепи сопротивление проводов обозначается резистором R_экв.пр. До подсоединения электрического нагревательного прибора ток на резисторе R_экв.пр. и лампочке равен

I₁=I₂=I,

т.к. соединение последовательное. Напряжение на зажимах лампочки найдем из формулы:

(2)

+ R_экв.пр

I₁

U₀ I₂

-

где U₀ численно равно э.д.с. источника, т.к. внутреннее сопротивление r=0, отсюда U₀=const.

Рассмотрим второй случай, напряжение на зажимах лампочки найдем из формулы:

Отсюда

(3)

Найдем

+ R_экв.пр

I₁ l

U₀ I_H

-

l

вычтя почленно уравнения (2) и (3), получаем

С учетом формулы (1), получаем

Вычисления:

Ответ: напряжение на зажимах лампочки понизится на U=6,8 В.

Задача 45

От батареи с э.д.с. Е=500 В требуется передать энергию на расстояние l=2,5 км. Потребляемая мощность Р=10 кВт. Найти минимальные потери мощности в сети, если диаметр медных подводящих проводов d=1,5 см.

Дано: Е=500 В l=2500 м d=0,015 м Р=104 Вт	Решение: Общая длина проводов 2l. Сопротивление проводов найдем из формулы
Р – ?	Силу тока в цепи найдем из формулы:

E

R

(2)

Минимальная потеря мощности Р в цепи может быть найдена из формулы

(3)

Подставляем (1) и (2) в (3), получаем

(4)

Площадь поперечного сечения проводника

(5)

где R – радиус сечения.

Подставим (5) в (4), получаем

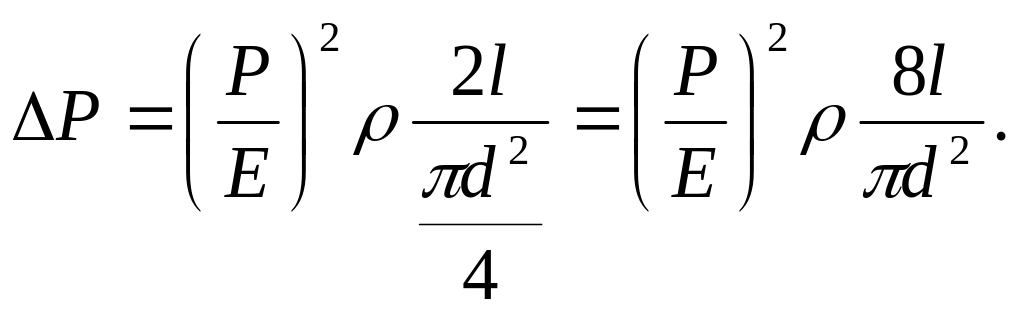
Вычисления:

Ответ: минимальная потеря мощности в сети равна

Задача 46

Элемент с эдс Е=6В дает максимальный ток I=3А. Найти наибольшее количество теплоты, которое может быть выделено на внешнем сопротивлении в единицу времени.

Дано: Е=6 В I=3 А	Решение: По закону Ома для полной цепи

ток максимален, когда R=0 (внешнее сопротивление).

(1)

Напряжение на зажимах источника, замкнутого проводником на сопротивление R, равно

E r

I

R

(2)

Количество теплоты Q_, выделенное во внешнем сопротивлении в единицу времени равно мощности во внешнем участке цепи

P=IU (3)

подставим (2) в (3), получаем

P(I) = P= I(E-Ir)=IE - I²r (4)

Для нахождения максимальной мощности во внешнем участке цепи необходимо найти производную выражения P=(I) по переменной I и приравнять полученное выражение к нулю.

P(I) = E-2Ir =0

E-2Ir (5)

При токе

(6)

мощность максимальна при R_общ=2r.Тогда R_внеш=r. Подставим (6) в (4) при R=r.

Получаем

Вычисления:

Ответ: наибольшее количество теплоты, которое может быть выделено на внешнем сопротивлении в единицу времени, составляет Дж/с.