33.Понятие и классификация индексов.

Индекс – это относительная величина, показывающая, во сколько раз уровень изучаемого явления в данных условиях отличается от уровня того же явления в других условиях.

В статистике для обозначения индексируемой величины применяется соответствующая символика:

- объем выпуска – q;

- цена – р;

- затраты времени на единицу продукции (трудоемкость) – t;

- выработка продукции в единицу рабочего времени – w;

- заработная плата – f;

- себестоимость – z;

- фондоотдача – Н;

- объем основных производственных фондов – Ф;

- численность работающих –T;

- товарооборот – Q;

- общие затраты (расходы) на производство – С;

- общий фонд оплаты труда – F.

Чтобы различать к какому периоду относится индексируемая величина, принято возле соответствующего символа ставить знаки: 1 – для отчетного периода; 0 – для периодов, с которыми сравниваются отчетные показатели.

Индексы делятся на :

1. Количественные ( объемные)- объем выполненной продукции, численность рабочих, фонд з/п

2. Качественные- показатели рассчитанные на единицу продукции ( цена, с/б, производительность труда)

34.Индивидуальные и общие индексы.

Относительная величина, получаемая при сравнении уровней, называется индивидуальным индексом, если исследователь не интересуется структурой изучаемого явления и количественную оценку уровня в данных условиях сравнивает с такой же конкретной величиной уровня этого явления в других условиях.

Пример:

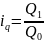
С аналитической точки зрения индекс объема показывает во сколько раз увеличится или уменьшается общая сумма выручки под влиянием изменения объема продажи в натуральных единицах.

Аналогично индекс цен показывает во сколько раз изменилась общая сумма выручки под влиянием изменения цены товара.

Индивидуальные индексы:

1. Индивидуальный индекс физического объема продукции- показывает, во сколько раз возрос (уменьшился) выпуск какого-либо одного товара в отчетный период по сравнению с базисным или сколько процентов составляет рост (снижение) выпуска товара

2. Индивидуальный индекс цен характеризует изменение цены одного определенного товара в текущий период по сравнению с базисным.

3. Индивидуальный индекс себестоимости единицы продукции показывает изменение себестоимости одного определенного вида продукции в текущий период по сравнению с базисным.

4. Индекс количества продукции, произведенной в единицу времени

5. Индекс производительности труда по трудовым затратам

6. Индивидуальный индекс стоимости продукции

Если известно, что изучаемое явление неоднородно и сравнение уровней можно провести только после приведения их к общей мере, экономический анализ выполняют посредством так называемых общих (сводных) индексов.

Основные элементы общих индексов:

- индексируемая величина (признак, значение которого является объектом изучения);

- коэффициент соизмерения (весы). С его помощью переводятся в сопоставимый вид разнообразные элементы.

35.Агрегатная и средняя формы общих индексов.

Индекс физического объема. (количественных показателей)

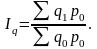Рассчитанный по данной формуле индекс физического объема продукции показывает, во сколько раз изменился физический объем продукции или сколько процентов составляет его уменьшение (рост) в текущем периоде по сравнению с базисным.

Разность между числителем и знаменателем индекса 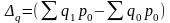свидетельствует об абсолютном росте 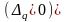или абсолютном уменьшение 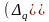стоимости выпущенных товаров в текущем периоде по сравнению с базисным периодом в сопоставимых ценах на уровне базисного периода.

Индексы ценВ международной статистической практике в настоящее время наиболее широко применяются формулы индексов цен Ласпейреса (с базисными весами), Пааше (с текущими весами) и Фишера. В 1871 г. немецким экономистом Е. Ласпейресом предложен индекс цен Ласпейреса, где в качестве соизмерителя используется объем продукции по разновидности в базисном периоде q₀. Индекс Ласпейреса рассчитывается по формуле:

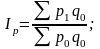
Индекс цен Пааше предложен в 1874 г. немецким экономистом Г. Пааше. В индексе в качестве соизмерителя используется объем продукции соответствующего вида в текущем периоде q₁. Индекс Пааше рассчитывается по формуле:

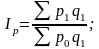Учитывая имеющееся несоответствие между индексами Паше и Ласпейреса, И.Фишером в международном сопоставлении предложен «идеальный индекс» (индекс Фишера), как среднегеометрическая величина из двух вышеупомянутых индексов:

.

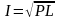Индекс себестоимости продукции рассчитывается по формуле:

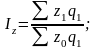
Рассчитанный по данной формуле индекс себестоимости продукции показывает, во сколько раз уменьшился (увеличился) в среднем уровень себестоимости продукции, произведенную в текущем периоде, или сколько процентов составляет его уменьшение (рост) в текущем периоде по сравнению с базисным.

Разность между числителем и знаменателем индекса 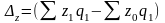характеризует экономию (-) или перерасход (+) от изменения себестоимости единицы продукции.

Индекс производительности труда по расходам на единицу продукции рассчитывается по формуле:

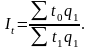
Существует две формы средневзвешенных индексов: среднеарифметическая и среднегармоническая. Как правило, средний арифметический индекс применяется при индексации количественных показателей (например, физического объема продукции), а средний гармонический – при индексации качественных показателей (например, цен). Например, необходимо вычислить общий индекс физического объема продукции I_q , когда по исходным данным известны индивидуальные индексы физического объема (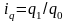 ) и стоимость продукции каждого вида за базисный период (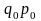 ). Тогда общий индекс физического объема продукции можно определить как среднюю арифметическую взвешенную из индивидуальных индексов. Для этого заменяем неизвестное количество продукции отчетного периода (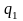 ) произведением . 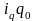Тогда общий индекс физического объема продукции приобретет вид:

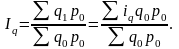
Если индексируемая величина выражается через индивидуальный индекс в знаменателе, то индекс имеет название среднего гармонического индекса.