21.Структурные средние.
Особый вид средних показателей – структурные средние. Они используются при изучении внутреннего строения рядов распределения значений признака. К ним относятся мода и медиана.
Мода и медиана характеризуют значение признака у статистической единицы, занимающей определенное положение в вариационном ряду.
Мода (Mo) - наиболее часто встречаемое значение признак в совокупности. Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и др.
Медиана (Me) - значение признака у статистической единицы, стоящей в середине ранжированного ряда и делящей совокупность на две равные по численности части.
Для
дискретных вариационных рядов Mo
и
Me
выбираются
в соответствии с определениями: мода -
как значение признака с наибольшей
частотой\
ni
;
положение медианы при нечетном объеме
совокупности определяется ее номером
,
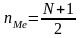где N
– объем статистической совокупности.
При четном объеме ряда медиана равна
средней из двух вариантов, находящихся
в середине ряда.
Мода определяется следующим образом:
• По максимальному значению частоты определяется интервал, в котором находится значение моды. Он называется модальным.
• Внутри модального интервала значение моды вычисляется по формуле:
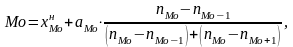
где
-
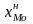нижняя граница модального интервала;
aМо - ширина модального интервала;
nМо , nМо-1, nМо+1 - соответственно частоты модального, предмодального (предшествующего модальному) и постмодального (следующего за модальным) интервалов.
Для расчета медианы в интервальных рядах используется следующий подход:
• По накопленным частотам находится медианный интервал.
Медианным называется интервал, содержащий центральную единицу.
• Внутри медианного интервала значение Me определяется по формуле:
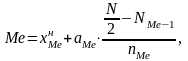
где
-
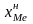нижняя граница медианного интервала;
aМе -ширина медианного интервала;
N – объем статистической совокупности;
N Ме-1- накопленная частота предмедианного интервала;
n Ме - частота медианного интервала.
22.Статистические ряды распределения и принципы их построения.
Статистический ряд распределения – это такое распределение единиц статистической совокупности по значению какого либо признака, при котором каждому значению или группе значений этого признака соответствует некоторое число единиц совокупности. Статистический ряд может быть формализован (представлен) как в табличном, так и графическом виде.
Атрибутивными называют ряды распределения, построенные по качественным признакам. Вариационными называют ряды распределения, построенные по количественному признаку.
В зависимости от характера вариации признака различают дискретные и интервальные вариационные ряды.
Дискретные вариационные ряды основаны на величинах признаков, которые имеют целые значения (например, тарифный разряд рабочих, количество марок автомобилей и т.п.).
В случае непрерывной вариации (интервального вариационного ряда) величина признака у единиц совокупности может принимать в определенных пределах любые значения, отличающиеся друг от друга (например, распределение заработной платы работающих в организации, распределение основных фондов предприятия и т.п.).