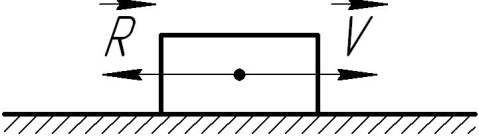
- •1.1.16 Матеріальна точка масою m рухається в площині Оху згідно рівнянь , , де b і с – сталі. Визначіть модуль рівнодійної сил, прикладених до точки.
- •1.1.30 Вагон скочується по прямолінійній колії, нахиленій до горизонту під кутом згідно рівняння (м). Визначіть силу гальмування f вагона, якщо його вага дорівнює р.
- •1.2 Визначення сил по заданому закону руху диференціальними рівняннями руху точки в проекціях на натуральні осі координат (перша задача динаміки)
- •1.3 Визначення параметрів прямолінійного руху по заданих силах (друга задача динаміки)
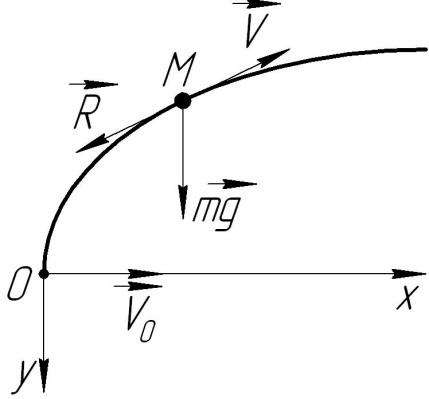
- •1.3.41 Снаряд вагою р вилітає зі швидкістю Vо під кутом до вертикалі. Запишіть диференціальне рівняння і початкові умови руху снаряда.
- •1.4 Визначення параметрів криволінійного руху по заданим силам (друга задача динаміки)
- •1.4.9 Матеріальна точка м рухається по криволінійній траєкторії під дією сили (н). Визначіть масу точки, якщо в момент часу 20 с її пришвидшення м/с2.
- •2.3.2 Теорема про зміну кількості руху
- •2.3.2.2 На матеріальну точку масою 1кг діє сила постійного напрямку, значення якої змінюється за законом н. Визначити швидкість цієї точки в момент часу , якщо початкова швидкість точки .
- •2.3.2.5 На матеріальну точку масою діє сила (н). Визначити проекцію на вісь oYшвидкості точки в момент часу , якщо вона рух починала зі стану спокою.
- •2.3.2.6 Матеріальна точка м масою 1кг рухається по прямій під дією сталої сили . Швидкість точки за проміжок часу , де , , змінилася від , . Визначити модуль сили .
- •2.3.2.7 Матеріальна точка м рухається по вертикалі під дією тільки сили ваги. Визначити, через який час точка досягне максимальної висоти, якщо її початкова швидкість
- •2.3.2.14 Тілу, що ковзає по гладким похилим напрямним, надана початкова швидкість м/с. Визначити, через який час тіло досягне максимальної висоти підйому.
- •2.3.2.15 Тіло, якому надали початкову швидкість м/с, опускається по гладким похилим напрямним. Визначити, через який час швидкість цього тіла досягне величини 9,81м/с.
- •2.3.2.16 Тіло, якому надали початкову швидкість м/с, ковзає по шорсткій горизонтальній площині і зупиняється через 1с. Визначити коефіцієнт тертя ковзання.
- •2.5 Теорема про зміну кінетичної енергії
- •2.5.1 Робота і потужність сили
- •2.5.1.2 На тіло діє постійна за напрямком сила
- •2.5.1.16 Моторний човен пливе по річці зі швидкістю 8м/с. Сила тяги двигуна дорівнює 3500н. Визначити в кВт потужність сили тяги двигуна.
- •2.5.5 Теорема про зміну кінетичної енергії матеріальної точки твердого тіла при поступальному русі
- •2.5.6 Теорема про зміну кінетичної енергії твердого тіла
- •2.5.7 Теорема про зміну кінетичної енергії механічної системи
- •3 Динаміка твердого тіла
- •3.1 Диференціальні рівняння обертання твердого тіла навколо нерухомої осі
- •6 Загальне рівняння динаміки
- •6.1 Застосування загального рівняння динаміки для опису руху системи сил
- •6.1.16 Визначити пришвидшення центра с котка 1, якщо тіла 1 і 2 – однорідні суцільні циліндри з однаковими масами і радіусами.
- •6.1.30 З яким пришвидшенням a падає вниз центр барабана масою m, що рівномірно розподілена по його ободу радіусом r, під дією власної ваги.
1.3 Визначення параметрів прямолінійного руху по заданих силах (друга задача динаміки)
1.3.1 Тіло рухається вниз по гладкій площині, яка нахилена під кутом = 300 до горизонту. Визначіть пришвидшення тіла.
а)
|
|
1.3.2 Тіло рухається вниз по шорсткій площині, яка нахилена під кутом = 300 до горизонту. Визначіть пришвидшення тіла, якщо коефіцієнт тертя ковзання дорівнює f = 0,2.
б) 3,2 м/с2;
|
|
1.3.3 Матеріальна точка М масою m = 5 кг рухається під дією сил F1 = 3Н і F2 = 10Н. Визначіть проекцію пришвидшення точки на вісь Ох.
в) 1,13 м/с2;
|
|
1.3.4
Матеріальна
точка М
масою m
= 9 кг рухається під дією сили
 .
Визначіть модуль пришвидшення точки.
.
Визначіть модуль пришвидшення точки.
г) а 1,17 м/с2
1.3.5 Тіло М масою m = 5 кг рухається вниз по гладкій площині під дією сил F = 10 Н, напрямок якої паралельний напрямку швидкості. Площина нахилена під кутом = 300 до горизонту. Визначіть пришвидшення тіла.
д) 6,9 м/с2. |
|
1.3.6
Тіло
М
масою m
= 200 г із стану спокою рухається вгору
по гладкій похилій площині під дією
сили F
= 1Н. Визначіть час, за який тіло
переміститься на відстань S
= 8 м, якщо
 .
.
д) t 13 с. |
|
1.3.7 Матеріальна точка М масою m = 900 кг рухається по горизонтальній прямій під дією сили F = 270 t (Н), яка спрямована по тій же прямій. Визначіть швидкість точки в момент часу t = 10 с, якщо в початковий момент часу t0=0 швидкість дорівнювала V0 = 10 м/с.
б) V = 25 м/с;
|
|
1.3.8
Матеріальна
точка М
масою m
= 25 кг почала рух із стану спокою по
горизонтальній прямій під дією сили
 (Н), яка спрямована по тій же прямій.
Визначіть шлях, пройдений точкою за час
t
=
4 с.
(Н), яка спрямована по тій же прямій.
Визначіть шлях, пройдений точкою за час
t
=
4 с.
в) S = 8,53 м;
|
|
1.3.9 Матеріальна точка М масою m = 100 кг рухається по горизонтальній прямій під дією сили F = 10 t (Н), яка спрямована по тій же прямій. Визначіть час, за який швидкість точки збільшиться з 5 до 45 м/с.
г) t = 20 с;
|
|
1.3.10 Матеріальна точка М рухається із стану спокою вниз по гладкій площині, яка нахилена під кутом = 100 до горизонту. Визначіть, за який час точка пройде шлях S = 30 м.
д) t 5,93 с. |
|
1.3.11 Тіло М масою m = 12 кг із стану спокою рухається по горизонтальній прямій під дією сили F = 0,6 t (Н), яка спрямована по тій же прямій. Визначіть шлях, пройдений тілом через t = 10 с після початку руху.
а) х 8,33 м;
|
|
1.3.12 Матеріальна точка М масою m = 0,25 кг рухається вздовж осі Ох під дією сили F = – 0,4t (Н). Визначіть швидкість точки в момент часу t = 2 с, якщо її початкова швидкість Vх0 =6 м/с.
б) V = 2,8 м/с;
|
|
1.3.13 Визначіть шлях, пройдений матеріальною точкою М масою m по осі Ох за час t = 1 с, якщо вона рухається під дією сили F = 12тt2 (Н). В момент часу t = 0 координата х0 =3 м, швидкість Vх0 = 6 м/с.
в) х = 10 м;
|
|
1.3.14
Матеріальна
точка М
масою m
= 2 кг рухається по горизонтальній осі
Ох
під дією сили
 (Н). Визначіть швидкість точки в момент
часу t
= 4 с, якщо при
t
= 0 швидкість V0
= 0.
(Н). Визначіть швидкість точки в момент
часу t
= 4 с, якщо при
t
= 0 швидкість V0
= 0.
г) V = 0 м/с;
|
|
1.3.15
Матеріальна
точка
М
масою m
= 50 кг із стану спокою рухається по
гладкій горизонтальній напрямній під
дією сили F
= 50 Н, вектор якої утворює постійний кут
 з напрямною. Визначіть шлях, пройдений
точкою за час t
= 20 с.
з напрямною. Визначіть шлях, пройдений
точкою за час t
= 20 с.
д) S 188 м. |
|
1.3.16 Тіло масою m = 200 кг після поштовху рухається прямолінійно, долаючи опір R = 4V2. Визначіть пришвидшення тіла, коли його швидкість V = 5 м.
а) а = -0,5 м/с2;
|
|
1.3.17 Матеріальна точка М масою m рухається по горизонтальній осі Ох під дією сили F = 2m(х+1) (Н). Визначіть пришвидшення точки в момент часу, коли її координата х = 0,5 м.
б) а = 3 м/с2;
|
|
1.3.18 На матеріальну точку М масою m = 200 кг, яка знаходиться на горизонтальній поверхні, діє вертикальна підйомна сила F = 10 t2 (Н). Визначіть час t, при якому почнеться рух точки.
в) t 14,0 с;
|
|
1.3.19 Тіло М масою m = 20 кг падає по вертикалі, сила опору повітря R = 0,04V2 (Н). Визначіть максимальну швидкість падіння тіла.
в)
|
|
1.3.20 По похилій площині із стану спокою починає ковзати тіло М масою m = 1 кг. Визначіть максимальну швидкість тіла, якщо сила опору руху R = 0,08V (Н).
г) = 41,9 м/с
|
|
1.3.21 Тіло М масою m = 1 кг падає по вертикалі, сила опору повітря R = 0,03V (Н). Визначіть максимальну швидкість падіння тіла.
д) = 327 м/с. |
|
1.3.22 Матеріальна точка М масою m = 7 кг із стану спокою рухається по осі Ох під дією сили F = 7 еt. Визначіть швидкість точки в момент часу t = 2 с.
а) V = 6,39 м/с;
|
|
1.3.23
На
матеріальну
точку
М
масою m
= 20 кг, яка рухається по горизонтальній
прямій, діє сила опору
 (Н).
За скільки секунд швидкість точки
зменшиться з 10 до 5 м/с.
(Н).
За скільки секунд швидкість точки
зменшиться з 10 до 5 м/с.
б) t = 10с;
|
|
1.3.24 Матеріальна точка М масою m = 4 кг рухається по горизонтальній прямій. Через скільки секунд швидкість точки зменшиться в 10 разів, якщо сила опору руху R =0,8 V2 і t0 початкова швидкість V0=3,6 м/с?
д) t = 12,5 с. |
|
1.3.25 На матеріальну точку М масою m = 250 кг, яка рухається по горизонтальній прямій, діє сила опору R = 5V2 (Н). Визначіть швидкість точки в момент часу t = 6 с, якщо при t0 = 0 її швидкість V0 = 20 м/c.
г) V = 5,88 м/с;
|
|
1.3.26 Точка М масою m рухається по осі Ох під дією сили Fх = 6m sіn(2t). В початковий момент часу швидкість точки VOх = 3 м/с. Визначіть сталу інтегрування в рівнянні швидкості.
д) С1 = 6. |
|
1.3.27 Матеріальна точка М масою m = 2 кг, яка рухається по горизонтальній осі Ох, під дією сили опору R= 5cоs(0,5t). Визначіть швидкість точки в момент часу t = 4 с, якщо при t0 = 0 її швидкість V0 = 0.
а) V = 4,55 м/с;
|
|
1.3.28
Запишіть
диференціальне рівняння руху і початкові
умови для точки М,
маса якої m
і яка знаходиться в однорідному полі
сил тяжіння, якщо точці надана початкова
швидкість Vо,
напрямлена
горизонтально, а під час руху на неї діє
сила опору
 .
.
б) |
|
|
|
|
|
|
||
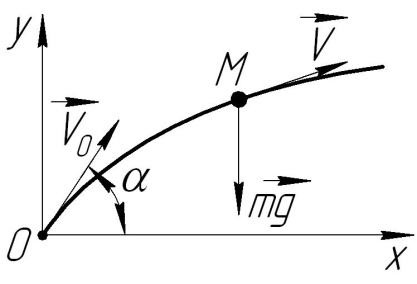
1.3.29 Точка М масою m вилітає з початковою швидкістю Vо під кутом до горизонту з точки О. Вкажіть диференціальне рівняння руху точки і відповідні початкові умови.
в) |
|
|
1.3.30 Точка М, маса якої m, випущена з висоти Н під кутом до горизонту з початковою швидкістю Vо . Запишіть диференціальне рівняння руху точки і відповідні початкові умови.
г) |
|
|
1.3.31 Снаряд М масою m вилітає з точки О зі швидкістю Vо під кутом до горизонту. Запишіть диференціальне рівняння руху снаряда і відповідні початкові умови, якщо сила опору повітря R = -kmV2.
д) |
|
|
1.3.32 Камінь М вагою Р кинули згори висотою Н пара-лельно осі Ох зі швидкістю Vо . Запишіть диференціальне рівняння руху каменя і початкові умови його руху.
б) |
|
|
|
|
|
|
|
1.3.33 Тіло М масою m падає з деякої висоти Н без початкової швидкості, долаючи опір середовища, сила якого R = kV2. Запишіть диференціальне рівняння і початкові умови руху тіла, якщо вісь Оу направлена вниз з початкового положення.
а)
|
|
|
1.3.34 Точка М, маса якої m, падає під дією сил тяжіння з висоти Н без початкової швидкості Vо. Запишіть диференціальне рівняння і початкові умови руху точки.
в)
|
|
1.3.35 Тіло М масою m ковзає по шорсткій похилій площині, з кутом до горизонту під дією сили тяжіння Р. Коефіцієнт тертя ковзання тіла до площини дорівнює f. Запишіть диференціальне рівняння і початкові умови руху тіла, якщо в початковий момент часу воно перебувало в стані спокою.
д)
|
|
1.3.36
Матеріальна
точка М
вагою Р
рухається із стану спокою вздовж
горизонтальної осі Ох
під дією сили
 ,
де k
– додатна стала. Запишіть диференціальне
рівняння і початкові умови руху тіла.
,
де k
– додатна стала. Запишіть диференціальне
рівняння і початкові умови руху тіла.
д)
|
|
1.3.37 Літак летить горизонтально на висоті Н зі швидкістю V. Запишіть диференціальні рівняння руху вантажа вагою Р, скинутого з цього літака без відносної початкової швидкості, і відповідні початкові умови, обравши початок координат у точці відокремлення вантажа від літака.
а)
|
|
1.3.38 Тіло М масою m = 2 кг кинуто вертикально вгору зі швидкістю Vо = 20 м/с. Сила опору руху тіла пропорційна швидкості і дорівнює R = 0,04V (Н). Визначте час, за який тіло досягне найвищого положення.
а) t 2 с;
|
|
1.3.39 Снаряд вагою Р масою m вилітає зі швидкістю Vо під кутом до горизонту. Сила опору повітря R = kV. Запишіть диференціальне рівняння і початкові умови руху снаряда.
в) |
|
|
1.3.40
Матеріальна
точка М
масою m
= 1 кг рухається вздовж горизонтальної
осі Ох
під дією сили
 (Н). Вважаючи початкові умови руху точки
нульовими, знайдіть координату х1,
точки в момент часу t1
= 1 с.
(Н). Вважаючи початкові умови руху точки
нульовими, знайдіть координату х1,
точки в момент часу t1
= 1 с.
г) х1 = (е – 2) м;
|
|


4,9 м/с2;
4,9 м/с2;







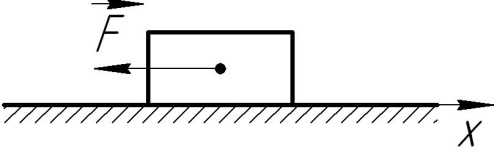



 = 70 м/с;
= 70 м/с;