- •1.1.16 Матеріальна точка масою m рухається в площині Оху згідно рівнянь , , де b і с – сталі. Визначіть модуль рівнодійної сил, прикладених до точки.
- •1.1.30 Вагон скочується по прямолінійній колії, нахиленій до горизонту під кутом згідно рівняння (м). Визначіть силу гальмування f вагона, якщо його вага дорівнює р.
- •1.2 Визначення сил по заданому закону руху диференціальними рівняннями руху точки в проекціях на натуральні осі координат (перша задача динаміки)
- •1.3 Визначення параметрів прямолінійного руху по заданих силах (друга задача динаміки)
- •1.3.41 Снаряд вагою р вилітає зі швидкістю Vо під кутом до вертикалі. Запишіть диференціальне рівняння і початкові умови руху снаряда.
- •1.4 Визначення параметрів криволінійного руху по заданим силам (друга задача динаміки)
- •1.4.9 Матеріальна точка м рухається по криволінійній траєкторії під дією сили (н). Визначіть масу точки, якщо в момент часу 20 с її пришвидшення м/с2.
- •2.3.2 Теорема про зміну кількості руху
- •2.3.2.2 На матеріальну точку масою 1кг діє сила постійного напрямку, значення якої змінюється за законом н. Визначити швидкість цієї точки в момент часу , якщо початкова швидкість точки .
- •2.3.2.5 На матеріальну точку масою діє сила (н). Визначити проекцію на вісь oYшвидкості точки в момент часу , якщо вона рух починала зі стану спокою.
- •2.3.2.6 Матеріальна точка м масою 1кг рухається по прямій під дією сталої сили . Швидкість точки за проміжок часу , де , , змінилася від , . Визначити модуль сили .
- •2.3.2.7 Матеріальна точка м рухається по вертикалі під дією тільки сили ваги. Визначити, через який час точка досягне максимальної висоти, якщо її початкова швидкість
- •2.3.2.14 Тілу, що ковзає по гладким похилим напрямним, надана початкова швидкість м/с. Визначити, через який час тіло досягне максимальної висоти підйому.
- •2.3.2.15 Тіло, якому надали початкову швидкість м/с, опускається по гладким похилим напрямним. Визначити, через який час швидкість цього тіла досягне величини 9,81м/с.
- •2.3.2.16 Тіло, якому надали початкову швидкість м/с, ковзає по шорсткій горизонтальній площині і зупиняється через 1с. Визначити коефіцієнт тертя ковзання.
- •2.5 Теорема про зміну кінетичної енергії
- •2.5.1 Робота і потужність сили
- •2.5.1.2 На тіло діє постійна за напрямком сила
- •2.5.1.16 Моторний човен пливе по річці зі швидкістю 8м/с. Сила тяги двигуна дорівнює 3500н. Визначити в кВт потужність сили тяги двигуна.
- •2.5.5 Теорема про зміну кінетичної енергії матеріальної точки твердого тіла при поступальному русі
- •2.5.6 Теорема про зміну кінетичної енергії твердого тіла
- •2.5.7 Теорема про зміну кінетичної енергії механічної системи
- •3 Динаміка твердого тіла
- •3.1 Диференціальні рівняння обертання твердого тіла навколо нерухомої осі
- •6 Загальне рівняння динаміки
- •6.1 Застосування загального рівняння динаміки для опису руху системи сил
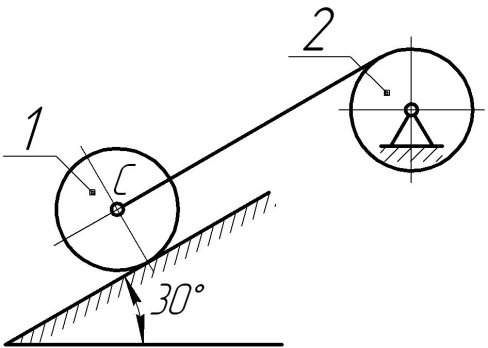
- •6.1.16 Визначити пришвидшення центра с котка 1, якщо тіла 1 і 2 – однорідні суцільні циліндри з однаковими масами і радіусами.
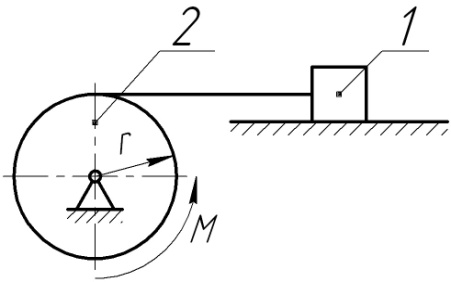
- •6.1.30 З яким пришвидшенням a падає вниз центр барабана масою m, що рівномірно розподілена по його ободу радіусом r, під дією власної ваги.
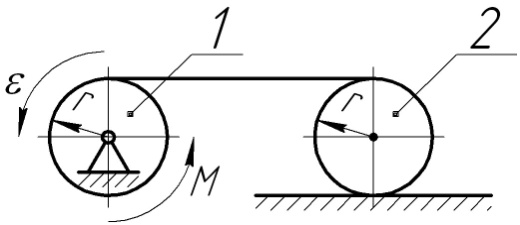
6.1.16 Визначити пришвидшення центра с котка 1, якщо тіла 1 і 2 – однорідні суцільні циліндри з однаковими масами і радіусами.
д) 2,45 м/с2. |
|
6.1.17 По горизонтальній платформі масою m=875кг біжить дитина з пришвидшенням ar = 2 м/с2 відносно платформи. Маса дитини m1 = 7,5 кг. Визначити пришвидшення платформи.
а) 0,017 м/с2;
|
|
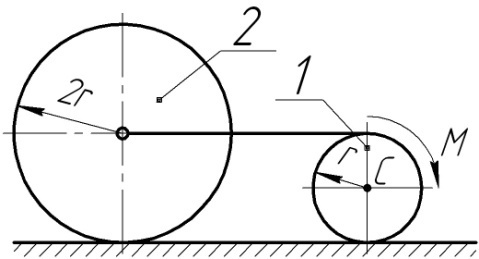
6.1.18 Однорідні суцільні циліндри з масами m2 =
= 2m1 = 100 кг рухаються по гладкій горизонтальній поверхні під дією пари сил з сталим моментом М=15Н·м, що прикладена до циліндра 1. Визначити пришвидшення центра С циліндра 1, коли r=0,2 м.
б) 0,111 м/с2;
|
|
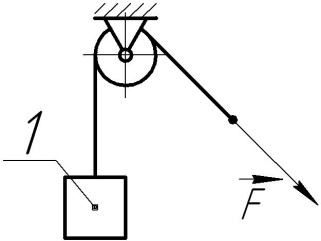
6.1.19 Визначити пришвидшення, з яким піднімається тіло 1 масою 10 кг під дією сили F, модуль якої 110 Н. При обчисленні приймати пришвидшення вільного падіння тіла g = 10 м/с2.
в) 1,0 м/с2;
|
|
6.1.20 Визначити пришвидшення тіла 1 масою 1 кг, що піднімається по шорсткій похилій поверхні під дією сили F, модуль якої дорівнює 6,75 Н. Коефіцієнт тертя ковзання f = 0,1.
в) 1,0 м/с2;
|
|
6.1.21 Балка 1 масою m1 = 200 кг лежить на валках 2 і 3, які можна вважати за однорідні циліндри масою m = = 20 кг. Визначити пришвидшення балки, що рухається під дією сили F= 440 Н.
г) 2,0 м/с2 |
|
6.1.22 Механічна система, що складається з барабана масою m = 20 кг, яка рівномірно розподілена по його ободу і двох вантажів 1 і 2 з масами m1=10 кг, m2=40кг, приводиться в рух парою сил з сталим моментом М = 50 Н·м. Визначити кутове пришвидшення барабана , якщо вважати, що вантажі 1 і 2 рухаються по ідеально гладким поверхням, а радіус r = 0,1 м.
д) 20 рад /с2. |
|
6.1.23 Механічна система складається з барабана, момент інерції якого відносно осі обертання J = 0,2 кг·м2 та двох вантажів з масами m1 = 10 кг, m2 = 40 кг. На барабан діє пара сил з сталим моментом М = 50 Н·м, причому вантажі рухаються по шорсткій поверхні. Визначити кутове пришвидшення барабана , якщо r=0,1м, а коефіцієнт тертя ковзання f = 0,1.
д) 21,7 рад /с2. |
|
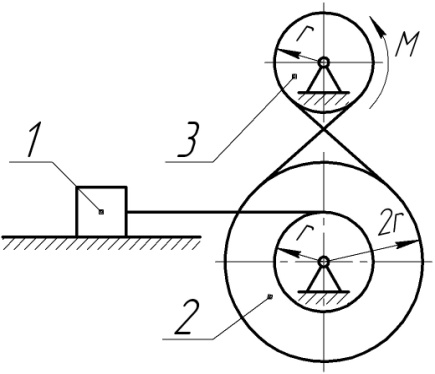
6.1.24 Визначити пришвидшення вантажа 1, маса якого m1 = 10 кг, що є складовою механічної системи, яка рухається завдяки парі сил з сталим моментом М=1,1 Н·м. Моменти інерції тіл 2 і 3 відносно осей обертання J2=0,04кг·м2, J3 = 0,02 кг·м2, радіус r = 0,1 м.
б) 1,0 м/с2;
|
|
6.1.25 З яким пришвидшенням підніматиметься тіло 1 під дією пари сил з сталим моментом М = 4,52 Н·м, якщо маси тіл m1 = m2 = 2 кг, радіус барабана r=0,2 м, який можна вважати однорідним циліндром.
в) 1,0 м/с2;
|
|
6.1.26 Визначити модуль кутового пришвидшення барабана , якщо він рухається під дією пари сил зі сталим моментом М = 0,06 Н·м. Маси тіл m1 = m2 = 1 кг, радіус r=0,2 м, барабан 1 вважати однорідним циліндром.
г) 1,00 рад/с2 |
|
6.1.27 Визначити пришвидшення тіла 1 масою m1=1кг, що рухається під дією моменту пари сил з модулем М = 5 Н·м. Момент інерції барабана 2 відносно осі обертання J2 = 1,0 кг·м2, радіус r = 0,5 м.
д) 2,0 м/с2. |
|
6.1.28 Визначити кутове пришвидшення барабана 1, що обертається під дією пари сил з сталим моментом М=0,14 Н·м. До барабана приєднаний коток 2 за допомогою нитки, що не деформується. Барабан 1 і коток 2 - однорідні циліндри з однаковим радіусом r = 0,2 м, маси тіл m1 = m2 = 2 кг.
а) 2,0 рад/с2;
|
|
6.1.29 З яким пришвидшенням a рухається вгору центр С однорідного котка з масою m = 20 кг під дією сили з модулем F = 128 Н.
б) 1,0 м/с2;
|
|