МГУИЭ

Кафедра сопротивления материалов.

Домашнее задание №2

по сопротивлению материалов.

«Изгиб бруса» Вариант – 13.

Работу выполнил:

Рузанов Леонид

Группа М-23

Проверил:

Митронов Владимир Ильич

2005 год.

Москва.

Расчётные схемы к задаче №1. Вариант -13.

Дано:

P = 2ql; m = ql2; l1 = k1l м; l2 = k2l м;

k1 = 0,4; k2 = 0,8;

Задача:

Для заданных расчётных схем балок построить эпюры внутренних силовых факторов Q и M_x в функции q и l (l₁ = k₁l; l₂ = k₂l; P = 2ql; m = ql²)

1 Балка

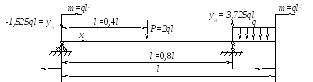
1. Найдём реакции опор:

Из условия равновесия

=>

=> (1)

=> =>

Подставим полученное значение y_B в уравнение (1):

2. Метод сечений:

1 сечение)

z₁

0 ≤ z₁ ≤ 0,4l;

Q_y1 = - y_A = -1,525ql;

Q_y1¹ = Q_y1² = -1,525ql;

M_изг1 = ql² – 1,525ql·z₁;

z₁ = 0 => M_изг1¹ = ql²

z₁ = 0,4l => M_изг1² = ql² - 1,525ql·0,4l= 0,39ql².

2 Сечение)

0 ≤ z₂ ≤ 0,4l;

Q_y2 = - y_A – 2ql= -1,525ql - 2ql = -3,525ql;

Q_y2¹ = Q_y2² = -3,525ql;

M_изг2 = ql² – 1,525ql·(0,4l + z₂) – 2ql·z₂;

z₂ = 0 => M_изг2¹ = ql² - 1,525ql·0,4l = 0,39ql²;

z₂ = 0,4l => M_изг2² = ql² - 1,525ql·0,8l - 2ql·0,4l = ql²(1- 1,22 - 0,8) = - 1,02ql².

3 Сечение)

0 ≤ z₃ ≤ 0,2l;

Q_y3 = - y_A – 2ql + y_B - qz₃= -1,525ql - 2ql + 3,725ql - qz₃ = 0,2ql - qz₃;

z₃ = 0 => Q_y3¹ = 0,2ql;

z₃ = 0,2l => Q_y3² = 0;

M_изг3 = q·l² – 1,525·q·l·(0,8·l + z₃) – 2·q·l·(0,4·l + z₃) + y_B·z₃ - ½·q·z₃²;

z₃ = 0 => M_изг3¹ = ql² - 1,525·q·l·0,8l – 2·q·l·0,4l = - 1,02·q·l²;

z₃ = 0,2·l => M_изг3² = q·l² - 1,525·q·l² - 2·q·l·0,6·l + 3,725·ql·0,2l - ½·q·0,04·l² =

= ql²(1- 1,525 – 1,2 + 0,745- 0,02) = - ql²;

Построение эпюров внутренних силовых факторов Q и M_x в функции q и l.

2 БАЛКА

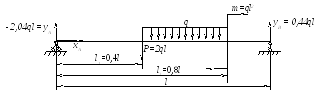
1. Найдём реакции опор:

Из условия равновесия

=>

=> (1)

=> =>

Подставим полученное значение y_B в уравнение (1):

2. Метод сечений:

1 сечение)

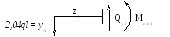
0 ≤ z₁ ≤ 0,4l;

Q_y1 = - y_A = - 2,04ql;

Q_y1¹ = Q_y1² = - 2,04ql;

M_изг1 = - 2,04ql·z₁;

z₁ = 0 => M_изг1¹ = 0

z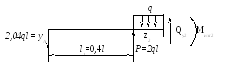₁ = 0,4l => M_изг1² = - 2,04ql·0,4l = - 0,82ql².

2 сечение)

0 ≤ z₂ ≤ 0,4l;

Q_y2 = - y_A + 2ql – qz₂ = -2,04ql + 2ql - qz₂

z₂ = 0 => Q_y2¹ = -2,04ql + 2ql = - 0,04ql

z₂ = 0,4l => Q_y2² = -2,04ql + 2ql – 0,4ql = -0,44ql;

M_изг2 = - 2,04ql(0,4l + z₂) + 2ql·z₂ - ½qz₂²;

z₂ = 0 => M_изг2¹ = - 2,04ql·0,4l = - 0,82ql²;

z₂ = 0,4l =>M_изг2² =-2,04ql·0,8l +2ql·0,4l -½q·0,16l ²=ql²(-1,63 +0,8 -0,08)=-0,91ql².

3 сечение)

0 ≤ z₃ ≤ 0,2l;

Q_y3 = - 2,04ql + 2ql -0,4ql;

Q_y3¹ = Q_y3² = - 2,04ql + 2ql -0,4ql = -0,44ql;

M_изг3 = - 2,04ql(0,8l + z₃) + P(0,4l + z₃) - 0,4ql(0,2l + z₃) + ql²;

z₃ = 0 => M_изг3¹ = - 2,04ql·0,8l + 2ql·0,4l - 0,4ql·0,2l + ql² = 0,09ql²;

z₃ = 0,2·l => M_изг3² = - 2,04ql² + 1,2ql² - 0,16ql² + ql²=0;

Построение эпюров внутренних силовых факторов Q и M_x в функции q и l.

3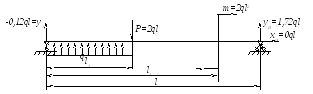 БАЛКА

1. Найдём реакции опор:

Из условия равновесия

=>

=> (1)

=> =>

Подставим полученное значение y_B в уравнение (1):

2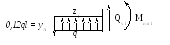. Метод сечений:

1 сечение)

0 ≤ z₁ ≤ 0,4l;

Q_y1 = - y_A + qz₁

z₁ = 0 => Q_y1¹ = -0,12ql

z₁ = 0,4l => Q_y1² = -0,12ql + 0,4ql = 0,28ql;

M_изг1 = - y_A·z₁ + q·z₁·½·z₁;

z₁ = 0 => M_изг1¹ = 0

z₁ = 0,4l => M_изг1² = - 0,12ql·0,4l+0,4ql·0,2l=0,03ql².

M_min1-? при z₁=? Q_y1 = - y_A + qz₁ = 0 => . Подставим полученное значение z₁ и найдём M_min1:

M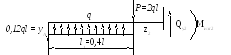_min1 = - 0,12ql·0,12l + q·0,12l·0,06l=0,0072ql² - 0,0144ql² = -0,0072ql²

2 сечение)

0 ≤ z₂ ≤ 0,4l;

Q_y2 = - 0,12ql + 0,4ql - 2ql= - 1,72ql;

Q_y2¹ = Q_y2² = -1,72ql;

M_изг2 =- y_A·(l₁ + z₂) + 0,4ql·(½·l₁ + z₂) - Pz₂ = - y_A·(0,4l + z₂) + 0,4ql·(0,2l+ z₂) – 2qlz₂

z₂ = 0 => M_изг2¹ = - 0,12ql·0,4l + 0,08ql² = 0,03ql²;

z₂ = 0,4l =>M_изг2² = - 0,12ql·0,8l + 0,24ql² - 0,8ql² = -0,66ql².

3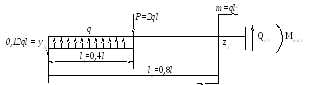 сечение)

0 ≤ z₃ ≤ 0,2l;

Q_y3 = - 0,12ql + 0,4ql - 2ql = - 1,72ql;

Q_y3¹ = Q_y3² = -1,72ql;

M_изг3 = - y_A·(0,8l + z₃) + 0,4ql·(0,6l + z₃) - 2ql·(0,4l + z₃) + ql²=

= - 0,12ql·(0,8l + z₃) + 0,4ql·(0,6l + z₃) - 2ql·(0,4l + z₃) + ql²;

z₃ = 0 => M_изг3¹ = - 0,12ql·0,8l + 0,4ql·0,6l - 2ql·0,4l + ql² = 0,34ql²;

z₃ = 0,2·l => M_изг3² = - 0,12ql² + 0,32ql² – 1,2ql² + ql²=0;

Построение эпюров внутренних силовых факторов Q и M_x в функции q и l.

Q_y

0,ql

-0,12

-1,72

-0,66

0,ql²

0,34

0,28

-1,72

-0,0072

0,12l

M_изг

0,03

-1,72

Расчётная схема к задаче №2. Вариант -13.

Дано:

P = 2ql; m = 3ql2; l1 = k1l м; l2 = k2l м;

k1 = 0,4; k2 = 0,8;

Задача:

Для заданной расчётной схемы рамы построить эпюры внутренних силовых факторов Q_y, N_z и M_x в функции q и l (l₁ = k₁l; l₂ = k₂l; P = 2ql; m = 3ql²)

=>

=> (1)

=> =>