2. Построение эпюр внутренних усилий в рамах

При построении эпюр Q, M и N условимся придерживаться следующих правил:

1. Опорные реакции необходимо показать на схеме всей рамы или отдельных ее частей. Желательно предугадать действительное направление опорных реакций.

Если это не получится и опорные реакции имеют отрицательное значение, то следует изменить их направление на обратное и в последующем учитывать со знаком плюс.

2. При определении составляющих опорных реакций необходимо выбирать рациональный порядок составления уравнений, стремясь к тому, чтобы в каждое уравне­ние входило возможно меньше неизвестных (лучше по одному).

3. Построение эпюр следует начинать с эпюры изгибающих моментов М.

• Изгибающий момент в сечении рамы вычисляется как алгебраичес­кая сумма моментов, относительно центра тяжести сечения, всех сил, приложенных к отсеченной части. Ординаты эпюры изгибающих моментов откладываются со стороны растянутого волокна.

• Поперечная сила в сечении рамы вычисляется как алгебраическая сумма проекций сил, приложенных к отсеченной части, на нормаль к оси элемента в рассматриваемом сечении.

• Продольная сила в сечении рамы вычисляется как алгебраическая сумма проекций сил, приложенных к отсеченной части, на ось стержня.

П равила знаков для усилий выбираются следующим образом. Одна из сторон всех стержней отмечается штриховой линией, кото­рая условно обозначает низ стержня.

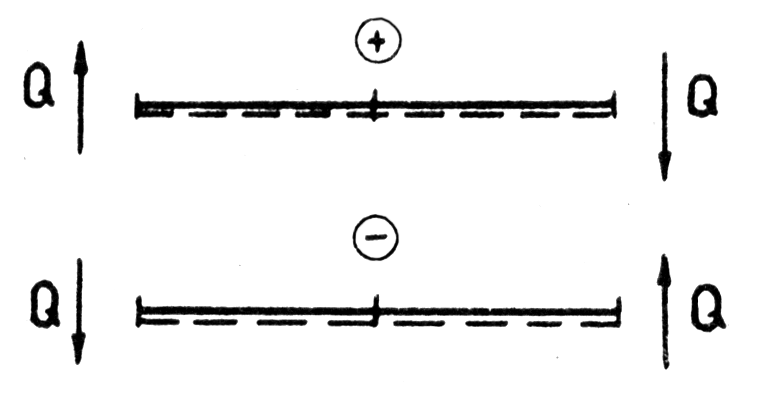
Рис.4.1. Правило знаков для М

Изгибающий момент считается положительным, если растянутым оказывается волокно, расположенное со стороны штриховой линии (рис.4.1.).

• П оперечная сила Q считается положительной, если проекция на нормаль к оси стержня равнодействующих сил, приложенных к левой отсеченной части стержня, направлена вверх (по часовой стрелке относительно сечения) (рис.4.2.).

Рис. 4.2. Правило знаков для Q

• Продольная сила считается положительной в случае растяжения (рис. 4.3.).

Рис. 4.3. Правило знаков для N

Штриховая линия, проводимая вдоль одной из сторон стержня рамы, условно обозначает низ стержня. Эта линия может быть проведена с любой стороны стержня. Для горизонтальных и наклонных стержней удобно проводить штриховую линию снизу.

Положительные ординаты эпюры М откладываются со стороны штриховой линии, положительные ординаты эпюр Q и N – со стороны, противоположной низу стержня (штриховой линии).

Усилия в стержнях, вплотную примыкающих к узлам рамы, следует обозначать принятыми буквами (М, Q, N), сопровождая их индексами в соответствии с названием узла и номера стержня.

Например:

M _c2 = –32 кН – изгибающий момент во втором стержне в сечении, примыкающем к узлу С (рис.4.4.).

Рис. 4.4. Эпюра моментов

Q_с2 – поперечная сила во втором стержне в сечении, примыкающем к узлу С.

Построение эпюры необходимо проверить как с точки зрения соответствия всех эпюр характеру нагрузок, так и с точки зре­ния равновесия всех узлов, отдельных частей и всей рамы в целом.

При проверке соответствия всех эпюр характеру нагрузок необходимо руководствоваться следующим:

Для эпюры М:

• в пределах незагруженного участка прямолинейного стержня эпю­ра должна изменяться по линейному закону;

• в месте приложения сосредоточенной силы эпюра имеет излом по направлению действия этой силы;

• в месте приложения сосредоточенного момента эпюра имеет скачок, равный по величине этому моменту;

• на участках воздействия равномерной нагрузки эпюра изображает­ся параболой, выпуклость которой обращена в сторону действия нагрузки;

• в шарнирах изгибающие моменты должны быть равны нулю.

Для эпюры Q:

• в пределах незагруженного прямолинейного участка стержня зна­чение Q должно быть постоянным;

• в местах приложения сосредоточенной силы эпюра имеет скачок, равный проекции силы на нормаль к оси стержня;

• на прямолинейной участке, загруженном равномерной нагрузкой, эпюра меняется по линейному закону;

• в тех сечениях стержня, где Q равна нулю или меняет знак, изгибающий момент должен иметь максимальное или минимальное значение.

Для эпюры N:

• в пределах незагруженного прямолинейного участка стержня или при нагрузке, действующей к оси стержня по нормали, значение N должно быть постоянным;

• в месте приложения сосредоточенной силы, направленной не по нормали к оси стержня, эпюра имеет скачок, равный проекции си­лы на ось стержня;

• на прямолинейном участке, загруженном равномерной нагрузкой, если она действует не по нормали к оси стержня, эпюра меняется по линейному закону.

4. При проверке равновесия узлов рамы следует выразить каждый ее узел сечениями, бесконечно близко расположенными к центру узла, приложить к узлу действующие на него сосредоточенные силы, сосредоточенные моменты и усилия М, Q и N, возникаю­щие в поперечных сечениях.

Рекомендуется векторы усилий, действующих на узел, показать с учетом их знаков и с указанием численного значения этих усилий. При этом следует учесть, что направление положительного момента должно быть таким, чтобы вызывать растяжение волокон стержня, отмеченных штриховой линией, положительное значение Q стремится вращать узел по часовой стрелке, а положитель­ное значение N вызывает растяжение.

При равновесии узла уравнения проекций на горизонтальную ось, уравнения проекций на вертикальную ось и уравнения момен­тов относительно центра узла при подстановке найденных значе­ний усилий должны обращаться в тождества.

5. Эпюры М, Q и N должны быть выполнены с обязательным численным обозначением характерных ординат на концах всех стержней, под сосредоточенными силами и моментами, в середине участка с распределенной нагрузкой.

6. Ось стержня принимается за ось абсцисс. Вычисленные ординаты эпюр откладываются перпендикулярно к оси рассматриваемого стержня. Положительные ординаты эпюры Q откладываются вверх от оси ригеля и влево от оси стойки. Знак на эпюре ставится.

Ординаты эпюры М откладываются со стороны растянутых волокон. Знак на эпюре не ставится.

Ординаты эпюры N откладываются симметрично по обе стороны от оси рассматриваемого стержня. Знак на эпюре N обязателен.

7. Штриховка эпюр производится перпендикулярно к оси стержня.

3. Пример 4.1.

Определить внутренние усилия и построить эпюры М, Q и N в простейшей стати­чески определимой раме, расчетная схема которой представлена на рис.4.5.

l₁ = 6 м; l₂ = 3 м; h₁ = 6 м; h₂ = 6 м;

F = 30 кН q = 2 кН/м

Рис. 4.5. Расчетная схема рамы

Решение.

1. Проверка статической определимости и геометрической неизменяемости рамы.

Определяем степень свободы системы по формуле:

n = 3Д – 2Ш – С_оn , (15)

где n – степень свободы системы;

Д – число дисков;

Ш – число простых шарниров, не считая опорных;

C_on – число опорных стержней.

n = 3 · 1 – 2 · 0 – 3 = 0

Степень свободы системы равна нулю. А так как рама представляет собой жёсткий диск, который прикреплен к земле с помощью трех стержней, оси которых не пересекаются в одной точке и не параллельны друг другу, то данная рама является системой статически определи­мой и геометрически неизменяемой.

2.Определение опорных реакций.

Освобождаем раму от опорных связей, а их действие заменяем реакциями отброшенных связей. Направление реакции шарнирно-неподвижной опоры А заранее указать нельзя, поэтому изображаем две взаимно перпендикулярные составляющие этой реакции Н_А и V_В.

Р еакция шарнирно-подвижной опоры «В» действует по вертикали вверх (рис.4.6.).

Рис. 4.6. Схема определения опорных реакций

Теперь раму можно рассматривать как свободное твердое тело, находящееся в равновесии под действием заданной нагрузки и трех неизвестных, составляющих реакции опор Н_А, V_A и V_В.

Для определения неизвестных необходимо составить три уравнения ста­тики, из совместного решения которых найдутся искомые величины.

Правильным выбором условий равновесия иногда удается уйти от реше­ния системы уравнений, свести задачу к решению независимых уравнений. Так в нашем примере правильным выбором условий равновесия мож­но добиться того, чтобы в каждое уравнение вошла лишь одна неизвестная величина. Это в значительной степени упростит решение задачи.

1. ∑Х = 0 –Н_А = 0 Н_А = F = 30 кН

2. ∑М_А = 0

3. ∑М_В = 0

Проверка. Для проверки правильности найденных значений реакций опор составим уравнения проекций на вертикальную ось:

∑У = 0 –V_A – q(l₁ + l₂) + V_В = –10,5 – 2(6 + 3) + 28,5 = 0

0 = 0

Произведенная проверка показывает, что реакции опор определены вер­но. При подстановке в уравнение найденных значений усилий получено тождество.

3. Определение изгибающих моментов и построение эпюры М.

При построении эпюры изгибающих моментов раму необходимо разбить на участки, в пределах которых выражения для изгибающего момента остается неизменным. Выражения для изгибающего момента будут меняться в сечениях, где:

а) приложена сосредоточенная сила или сосредоточенный момент;

б) начинается или заканчивается участок с распределенной нагрузкой;

в) происходит излом оси рамы.

Р азбивка рамы на участки показана на рис. 4.7.

Рис. 4.7. Разбивка рамы на участки

Номера участков обозначены цифрами. Штриховыми линиями показаны «нижние» волокна стержней.

Знак изгибающего момента определяется по его воздействию на «нижнее» волокно стержня в пределах рассматриваемого участка. Если «нижнее» волокно под действием изгибающего момента растянуто, то знак плюс, если сжато – минус.

Ординаты эпюры изгибающих моментов откладываются со стороны растянутого волокна.

Рассмотрим определение изгибающих моментов в раме по участкам.

I участок (рис. 4.8.).

Рис. 4.8. Участок I

0 м ≤ У₁ ≤ 3 м; М₁ = Н_А · У₁

Изгибающий момент имеет знак плюс, так как момент, создан­ный силой Н_А = 30 кН, вызывает растяжение «нижнего» волокна стержня.

Характер изменения изгибающего момента – прямая линия, для построения которой необходимо знать значения момента M₁ в двух точках:

У₁ = 0 м М_А1 = 30 · 0 = 0 кНм

У₁ = 3 м М_А1 = 30 · 3 = 0 кНм

II участок (рис. 4.9.). 3 м ≤ У₂ ≤ 6 м;

Р ис. 4.9. Участок II

М₂ = Н_А · У₂ – F(У₂ – 3)

У₂ = 3 м М_К2 = 30 · 0 – 30 ·(3 – 3) = 90 кНм

У₂ = 6 м М_С2 = 30 · 6 – 30(6 – 3) = 90 кНм

Сила Н_А создает положительный момент, сила F – отрицательный.

Х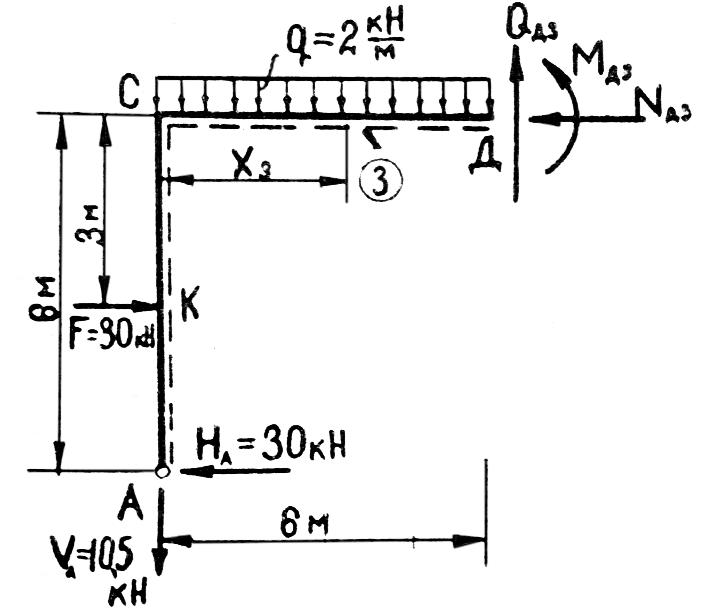 арактер эпюры – прямая линия.

III участок (рис. 4.10.). 0 м ≤ Х₃ ≤ 6 м;

Рис. 4.10. Участок III

Характер эпюры – кривая второго порядка, так как переменная Х₃ входит в выражение для М₃ во второй степени.

Х₃ = 0 м М_С3 = 30 · 8 – 10,5 · 0 – 30 · 3 – 2 · = 90 кН·м

Х₃ = 6м М_ДЗ = 30 · 6 – 10,5 · 6 – 30 · 3 – 2 · 6 · = –9 кН·м

Определим значение Х_{3 ,} при котором изгибающий момент М₃ имеет экстремальное значение. Для этого возьмем первую производ­ную от выражения для изгибающего момента М₃ по Х₃ и прирав­няем ее нулю:

П олученное значение X₃ = –5,25 м лежит за пределами рассматриваемого интервала [0; 6], поэтому на рассматриваемом участке функ­ция экстремума не достигает. Изгибающий момент монотонно убывает со значения 90 кНм в точке С до – 9 кНм в точке Д.

IV участок (рис. 4.11.).

Рис. 4.11. Участок IV

0 м ≤ Х₄ ≤ 3 м;

Характер эпюры – кривая второго порядка.

Х₄ = 0 м; М_Е4 = 0

Х ₄ = 3 м; М_Д4 =

V участок (рис. 4.12.).

Рис. 4.12. Участок V

0 м ≤ У≤ 6м; М₅ = 0

Изгибающий момент М₅ в любой точке по всей длине стержня равен нулю, так как к стержню приложена только одна внешняя сила V_в, линия действия которой совпадает с его осью, а, следовательно, плечо силы V_в равно нулю.

На основании полученных данных строим эпюру М (рис.4.13.) (Масштаб: в 1 см 20 кНм).

О т оси рамы откладываем найденные значения ординат и соединяем соответствующими линиями.

Рис. 4.13. Эпюра М

Статическая проверка правильности построения эпюры М.

Т ак как от действия моментов, вызываемых внешними силами, рама в целом находится в равновесии, то к каждая ее часть должна находиться в равновесии. Вырежем последовательно узлы рамы и проверим соблюдение условий их равновесия.

Узел С.

Рис. 4.14. Узел С

∑М_С = 0

М_С2 – М_С3 = 0

90 – 90 = 0

Из эпюры М видно, что в узле С действуют положительные моменты, поэтому при рассмотрении равновесия этого уз­ла векторы моментов прикладываем таким образом, чтобы они вызывали сжатие нижних волокон стержней (рис. 4.14.).

Условия равновесия узла выполнены.

У зел Д.

Рис. 4.15. Узел Д

∑Д = 0

–М_Д3 – М_Д4 = 0

–90 + 90 = 0

Условие равновесия узла вы­полнено.

Условия равновесия узлов выполнены, а это свидетельствует о том, что эпюра М построена верно.