Глава II
РАСЧЕТ МНОГОПРОЛЕТНЫХ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ (ШАРНИРНЫХ) БАЛОК
1. Общие сведения
Шарнирной балкой называется геометрически неизменяемая статически определимая система, составленная из расположенных в определенной последовательности однопролетных консольных и простых балок, соединенных между собой шарнирами. Шарнирную балку можно образовать из неразрезной (рис. 2.1), введя в ее пролеты шарниры.
Рис.2.1. Неразрезная балка
Число промежуточных шарниров Ш должно быть равно числу опорных стержней шарнирной балки Соп без трех, т.е.
Ш = Соп – 3 (4).
Следовательно, для предложенной неразрезной балки необходимо ввести: Ш = 6 –3 = 3 - промежуточных шарнира.
Формула (4) позволяет определить максимальное число промежуточных шарниров, при котором шарнирная балка еще может быть геометрически неизменяемой и статически определимой.
Например, для балки, изображенной на рис.2.1., во всех пролетах, за исключением любого одного, может быть установлено по одному шарниру (рис.2.2,а). Эту шарнирную балку можно расчленить на основную балку 4 и так называемые передаточные балки 1,2 и 3 (рис.2.2, б).
Схема 2.2.б называется схемой взаимодействия элементов шарнирных балок или поэтажной схемой.
а)
1
4
3
б)
Рис.2.2. а) Схема шарнирной балки
б) Поэтажная схема
Построение эпюр поперечных сил и изгибающих моментов
Конечным этапом статического расчета шарнирной балки является построение эпюр (графиков изменения по длине балки) поперечных сил (эпюры Q) и изгибающих моментов (эпюры М).
Поперечная сила в сечении балки численно равна алгебраической сумме проекций всех внешних сил (в том числе и реактивных), действующих по одну сторону от сечения, на ось, перпендикулярную к оси балки.
Изгибающий момент в сечении балки численно равен алгебраической сумме моментов всех внешних сил, действующих по одну сторону от рассматриваемого сечения, относительно его центра тяжести.
П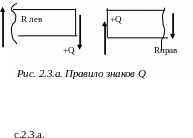
равила
знаков поперечной
силы и изгибающего момента ясны из
рис.2.3, а, б.
+М
+
+М
Рис. 2.3.б. Правило знаков М
При построении эпюры М у строителей принято ординаты, выражающие в определенном масштабе значения изгибающих моментов, откладывать со стороны растянутых волокон, т.е. положительные вниз, а отрицательные вверх от оси балки.
3. Пример 2.1.
Построить эпюры поперечных сил Q и изгибающих моментов M для балки, изображенной на рис.2.4.а.
Решение
Проверка геометрической неизменяемости.
В этой системе число опорных стержней Соп = 5, число промежуточных шарниров равно 2. Согласно формуле (3) максимальное число промежуточных шарниров, при котором данная система еще может быть неизменяемой
Ш = Соп – 3 = 5 – 3 = 2.
Производя анализ геометрической структуры системы, приходим к выводу, что она геометрически неизменяемая, так как в ней пролеты с двумя шарнирами расположены между пролетами без шарниров.
Проверка статической определимости.
Так как рассматриваемая система геометрически неизменяемая и содержит число промежуточных шарниров, удовлетворяющее условию (3), она статически определима.
Составление схемы взаимдействия элементов шарнирной балки (рис. 2.4,б). Рассматриваемая балка состоит из двух основных балок AD и FI, одной подвесной DF. Подвесная балка расчитывается первой.
P P P
A B C D E F G H I
А
а
)
1м 1м 1м 1м 1м 1м 1м
1м
A
B
C
D
E
F
G
H
I
б
)
