Решение

Так как Л = ЗК — Ш = 3∙1 —2 = 1, то рама один раз статически неопределима, т. е. содержит одну лишнюю связь.

Выберем основную систему, устранив нагрузку и горизонтальную связь в опоре В. Вертикальную связь отбросить нельзя, так как в противном случае оставшиеся три опорных стержня пересекутся в одной точке А и система будет мгновенно изменяемой.

Основная система, нагруженная заданной нагрузкой и неизвестной силой Х_1; заменяющей действие отброшенной связи, приведена на рис.7.6., б.

Каноническое уравнение в данном случае будет выражать условие равенства нулю суммарного горизонтального перемещения точки В от заданной нагрузки и неизвестной силы X₁:

Рассмотрим единичное состояние основной системы, когда по направле­нию удаленной связи приложена сила Х₁ = 1, а все остальные нагрузки отброшены (рис. 7.6., в). Вертикальные опорные реакции здесь равны нулю, а горизонтальную определим из уравнения ∑Х = 0:

откуда

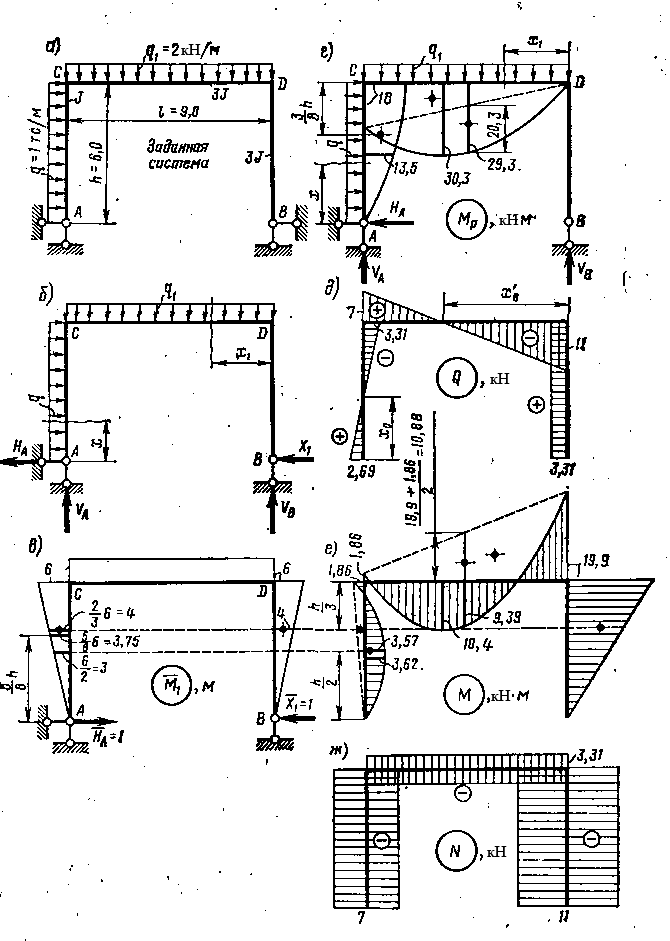
Рис. 7.6. Расчет рамы методом сил

Изгибающие моменты:

в сечениях элемента АС

в сечениях элемента CD

в сечениях элемента DB

Эпюра показана на рис. 7.6., в.

Далее изобразим грузовое состояние основной системы и построим эпю­ру М_р (рис. 7.6.,г). Сначала определим опорные реакции:

откуда

откуда

откуда

Изгибающий момент в произвольном сечении стойки АС:

Для определения максимального изгибающего момента найдем расстоя­ние до сечения, в котором Q = 0:

Изгибающий момент в произвольном сечении стойки АС:

В данном случае это сечение совпадает с сечением С, следовательно,

Изгибающий момент в произвольном сечении ригеля на расстояниях х₁ от точки D

Найдем расстояние до сечения, в котором Q = 0, а изгибающий момент имеет максимальное значение:

откуда х'_о = V_B/q_t = 11/2 = 5,5 м.

Тогда М_тах = 11∙5,5 — 5,5² = 30,3 кН∙м.

Для определения перемещения δ₁₁ умножим площади ω на ординаты у взятые из одной и той же эпюры

Перемножая эпюры М_р и М₁ для получения перемещения ∆_1p, из пер­вой возьмем площади, из второй — ординаты, соответствующие центрам тяжести этих площадей. При этом эпюру М_р по ригелю разобьем на две фигуры: треугольник (l = 9 м, h = 18 тс∙м) и площадь, ограниченную параболой (l = 9 м, h = 20,3 тс∙м).

Обозначения в скобках приняты согласно табл. 14;

Теперь можем найти значение силы Х₁:

Возвращаемся к системе, показанной на рис. 7.6.,б, вводя теперь уже известную силу X₁= 3,31 кН.

Сила X₁ в данном случае не вызывает вертикальных опорных реакций, так как проходит через центры обоих опорных шарниров. Поэтому эти ре­акции остаются такими же, как и при нагружении основной системы только заданной, нагрузкой (для получения эпюры М_р), т.е. V_A =7 кН, V_B = 11 кН. Значение же реакции Н_А изменится по сравнению со значением, полученным от указанного нагружения:

откуда

Переходим к вычислению поперечных сил:

Стойка АС

Q_A =Н_А = 2,69 кН; Q_C=H_A— qh= 2,69 — 1∙6 = — 3,31 кН

Ригель СD

Q_c= V_А = 7кН; Q_D=Va — q₁l = 7 — 2∙9 = —11 кН.

Стойка ВD

Q_B=X₁ = 3,31 кН; Q_D= Q_B = 3,31 кН

Эпюра Q показана на рис. 123,д.

Определяем изгибающие моменты;

Стойка АС

М_х = Н_Ах — qx²/2 = 2,69а: — 1∙x²/2= 2,69 x — 0,5 x ²;

при х = 0 М_А =0;

при х = 3 м М_х= 2,69∙3 — 0,5∙З² = 3,57 кН∙м;

при х = 6 м М_с = 2,69-6 —0,5-6² = —1,86 кН∙м.

Найдем расстояние х₀ до сечения, в котором изгибающий момент имеет максимальное значение. Приравняем для этого нулю поперечную силу в этом сечении, выраженную через х₀:

откуда x_o = H_A/q = 2,69/1 = 2,69 м.

Тогда

М_max = 2,69∙2,69 — 0,5∙2,69² = 3,62 кН∙м.

Ригель СD

Найдем расстояние х'_о до сечения с максимальным изгибающим момен­том. В этом сечении

Следовательно,

Стойка ВD

Эпюра М показана на рис. 7.6.,е.

Для проверки правильности ее построения вычислим горизонтальное перемещение точки В (∆_В(гор)), умножив площади этой эпюры на соответствующие ординаты из эпюры М₁. Если эпюра построена правильно, то ∆_В(гор) должно получиться равным нулю. Заменим эпюру М по стойке АС

двумя фигурами: треугольником (l =6м, h = 1,86 кН∙м) и площадью, ограниченной параболой (l =6м; h = 3,57 + 1,86/2 = 4,5 кН∙м), а по ригелю — трапецией и также площадью, ограниченной параболой (l = 9 м, h = 10,9 + 9,39 = 20,3 кН∙м). Разбивать трапецию на два тре­угольника или находить точное положение ее центра тяжести нет необхо­димости, так как в эпюре М₁ все ординаты по ригелю имеют одно и то же значение. Итак,

Следовательно, окончательная эпюра М построена правильно. Вычисляем продольные силы и строим эпюру N (рис. 7.6.,ж):

Т_ФС = — М_Ф = — 7 кН; т_св = — Х₁ = — 3б31 кН Т_ИВ= —М_И = — 11 кН.