17.Классификация связей. Действительные и возможные перемещения. Принцип возможных перемещений. Пример.

Классификация связей

• связи, не содержащие явно времени t, называются стационарными, в противном случае – нестационарными

• связи, выражающиеся в виде равенс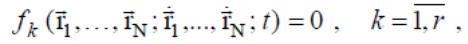тв вида , называются удерживающими, а в виде неравенств вида 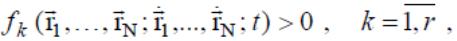– неудерживающими.

Удерживающие в свою очередь делятся на: а)геометрические(конечные) связи,которые накладывают ограничения только на положение системы, б) дифференциальные или кинематические связи, накладывающие ограничения как на положение точек, так и на их скорости. Дифференциальные

связи бывают интегрируемые (условие можно проинтегрировать) и неинтегрируемые.

Среди кинематических связей есть такие, которые путем их интегрирования могут быть превращены в геометрические, такие связи называются еще голономными. неинтегрируемые называются неголономными.

Рассмотрим бесконечно малые перемещения точек системы, совместимые со связями, наложенными на систему. Среди этих перемещений будем различать два вида перемещений - виртуальные и действительные. Действительные перемещения - это перемещения dr_k точек системы, которые они реально совершают за время dt.

Виртуальным перемещением δr_i называется мысленное бесконечно малое перемещение точки, допускаемое связями без их разрушения в данное фиксированное мгновение времени.

Принцип виртуальных перемещений: для равновесия механической системы, на которую наложены голономные, удерживающие, стационарные и идеальные связи, необходимо и достаточно, чтобы сумма работ всех активных сил, приложенных к точкам системы, на любом виртуальном перемещении равнялась нулю

Необходимость принципа следует из принципа Даламбера Лагранжа , так как в положении равновесия системы при Vi = 0 = const ускорения точек системы a = 0, следовательно, Фi = 0. Достаточность докажем методом от противного. Предположим, что не выполняется, а система находится в равновесии. Так как на систему наложены стационарные связи, то элементарные действительные перемещения точек системы совпадают с ее виртуальными перемещениями

Откуда из теоремы об изменении кинетической энергии следует, что T – T₀ <> 0, а это может быть только тогда, когда хотя бы одна точка системы движется. Таким образом, наше предположение не верно, а верно и достаточность принципа виртуальных перемещений доказана.

18.Принцип Даламбера для системы

Запишем дифференциальные уравнения несвободной сис-темы материальных точек в виде m_ia_i = F_i^e + F_iⁱ + R_i^e + R_iⁱ (i = 1÷n), где F_i^e и F_iⁱ - равнодействующие внешних и внутренних активных сил, приложенных к точке системы с номером i, а R_i^e и R_iⁱ - равнодействующие реакций внешних и внутренних связей, приложенных к той же точке.

Если ввести в рассмотрение силы инерции каждой точки системы Ф_i = -ma_i, то эти уравнения можно записать в виде

(4)

Система уравнений (4) выражает принцип Даламбера для системы материальных точек: если к активным силам (внешним и внутренним) и реакциям связей (внешних и внутренних), действующим на каждую материальную точку системы, добавить силу инерции точки, то в любое мгновение времени полученная система сил будет уравновешенной.

Однако для метода кинетостатики используют не сам принцип Даламбера, а его следствия, которые мы далее получим. Так как на каждую точку системы действует уравновешенная система сил, то сумма моментов этих сил относительно любого центра O (подвижного или неподвижного) равна нулю, то есть

(5)

Суммируем все уравнения системы (4) и системы (5). По свойству внутренних сил главные векторы и главные моменты внутренних активных сил и реакций внутренних связей равны нулю. Поэтому после суммирования имеем

(6)

где представлены главные векторы и главные моменты внешних активных сил, реакций внешних связей, сил инерции системы.

Таким образом, следствия из принципа Даламбера для системы материальных точек можно сформулировать так: при движении системы материальных точек геометрическая сумма главных векторов внешних активных сил, реакций внешних связей и сил инерции системы, а также геометрическая сумма главных моментов указанных сил относительно произвольного центра равны нулю в любое мгновение времени.

19. Принцип Даламбера-Лагранжа или общее уравнение динамики.

Рассматривая принцип как теорему, для его доказательства используем принцип Даламбера. Напомним, что он получен из дифференциальных уравнений несвободной системы материальных точек, которые записаны на основе второй аксиомы динамики (второго закона Ньютона) и аксиомы связей теоретической механики.

Запишем для каждой точки системы принцип Даламбера:

Умножим скалярно обе части этих выражений на виртуальные перемещения точек системы, а затем сложим между собой правые и левые части полученных выражений, в результате получим математическую запись принципа Даламбера-Лагранжа:

(1)

который можно сформулировать так: при движении любой материальной системы виртуальная работа активных сил, реакций связей и сил инерции системы равна нулю.

Принцип Даламбера-Лагранжа или общее уравнение динамики для систем с идеальными связями. Если все связи, наложенные на систему, являются идеальными, то выражение (1) принимает вид

(2)

то есть при движении системы с идеальными связями виртуальная работа активных сил и сил инерции системы равна нулю.