2.2. Основная теорема зацепления. Теорема Виллиса

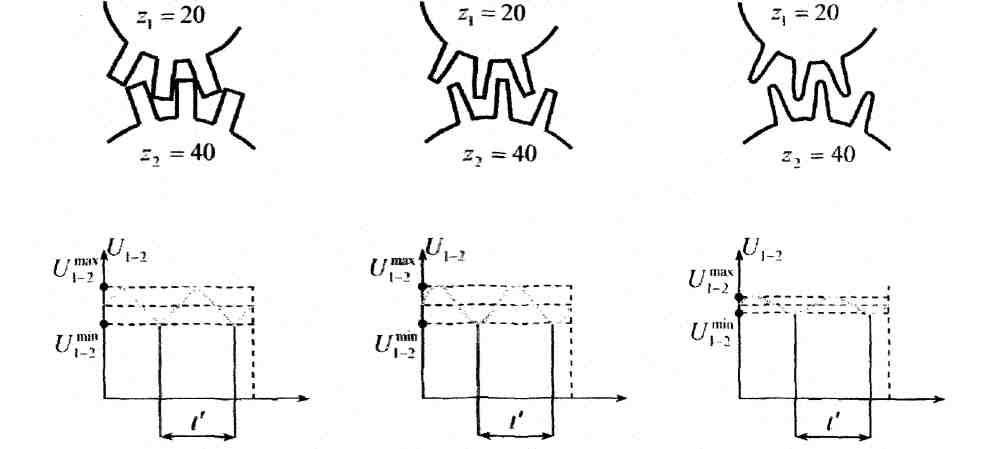
z₁=20, z₂ = 40.

t′ – время полного контакта двух сопряжено работающих зубьев, от встречи до расставания.

Внутри этого промежутка заметно, что передаточное отношение U_1–2 будет переменным.

Если зубчатая передача быстроходна, то такие передачи непригодны.

Теорема Виллиса

Какой кривой необходимо очертить профили зубьев, чтобы мгновенное передаточное отношение было постоянным?

Известны угловые скорости ω₁ и ω2₁.

.

Через точку А проведем общую касательную ТТ к сопряженным профилям. Разложим вектора скоростей на нормальные и тангенциальные составляющие, и сравним нормальные составляющие скоростей. Возможны следующие варианты:

1. > – первый профиль «внедрится» во второй, что приведет к их разрушению.

2. = – профили работают в контакте.

Так как , a , следовательно, , что допустимо и имеет место на практике. В процессе зацепления происходит не чистое обкатывание профилей, а соскальзывание, что приводит к износу зубьев по профилю.

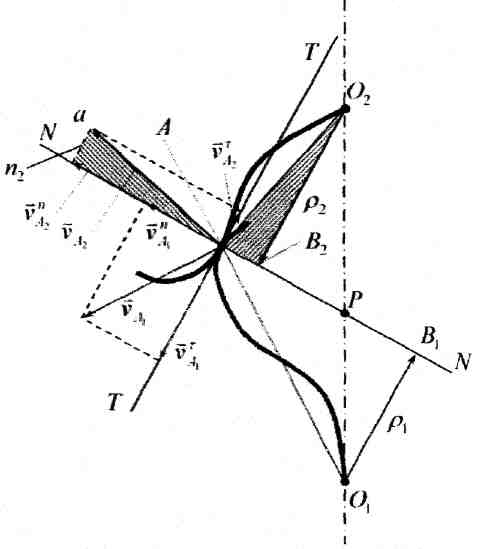
Сравним треугольники ∆О₂ В₂А и ∆Ап₂а. Эти треугольники подобны,

поэтому очевидно равенство , следовательно,

Обозначим

Аналогично

Исходя из того, что , получим

Рассмотрим треугольники ∆О₁В₁Р и ∆О₂В₂Р. Они подобны, как прямоугольные со смежными сторонами.

Обозначим О₁Р = r₁; О2₂Р = r₂. Тогда

Следовательно, положение точки Р на линии центров О₁О₂ в процессе

зацепления должно быть неизменным.

Для постоянства передаточного отношения в зубчатой передаче необходимо, чтобы общая нормаль NN к профилям зубьев всегда проходила бы через одну и ту же точку Р (полное зацепление) на линии центров О₁О₂ , и делила бы линию центров в отношении обратно пропорциональном отношению угловых скоростей. Следствия:

1. Чтобы в зубчатой передаче иметь постоянным передаточное отношение, необходимо профили зубьев очертить тонкими кривыми, которые отвечали бы требованиям основной теоремы зацепления.

2. Требованиям основной теоремы зацепления соответствует эвольвента, образующая эвольвентное зацепление и сочетание эпициклоиды и гипоциклоиды, образующей циклоидное зацепление.

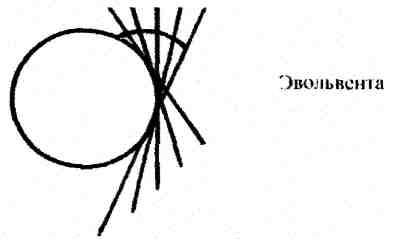
Эвольвента является бесконечной спиралью вне данной окружности. Проведем обкатывание вспомогательных окружностей D₁ и D₂ без скольжения по начальной окружности, и получим эпициклоиду и гипоциклоиду.

Ножка зуба оформляется по гипоциклоиде, а головка зуба оформляется по эпициклоиде.

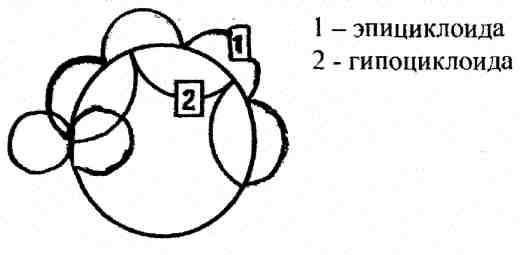
Таблица модулей по ГОСТ 9563-60

Таблица 2.1.

т — модули, мм
1-й ряд	2-й ряд
1	1,125
1,25	1,375
1,5	1,75
2	2,25
2,5	2,75
3	3,5
4	4,5
5	5,5
6	7
8	9
10	11
12	14