13.5. Шевронная передача

Цилиндрическое зубчатое колесо, венец которого по ширине состоит из участков с правыми и левыми зубьями, называется ш е в р о н н ы м.

Из технологических соображений шевронные колеса изготовляют двух типов с дорожкой посредине колеса (а) и без дорожки (б).

β

F_a/ F_a/

F^/ F^/

F_t/ F_t/

б)

Рис.13.4

В шевронном колесе осевые силы F_a/ на полушевронах, направлены в противоположные стороны, взаимно уравновешиваются внутри колеса и на валы и опоры валов не передаются. Поэтому у шевронных колес угол наклона зубьев принимают в пределах β =25^о...40^о, в результате чего повышается прочность зубьев, плавность работы передачи и ее нагрузочная способность. Поэтому шевронные колеса применяют в мощных быстроходных закрытых передачах.

Недостатком шевронных колес является высокая трудоемкость и себестоимость изготовления.

Лекция 14 Коническая зубчатая передача

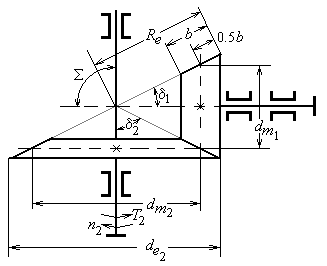
Конические передачи передают вращающий момент между валами с пересекающимися осями ( от 10⁰ до 170⁰, чаще всего под углом 90⁰). Их зубья бывают прямыми, косыми, круговыми и обычно имеют эвольвентный профиль.

Конические зубчатые передачи по сравнению с цилиндрическими имеют большую массу и габариты, сложнее в изготовлении, а также монтаже, так как требуют точной фиксации осевого положения зубчатых колес.

Наибольшее распространение имеют конические передачи с прямыми и криволинейными зубьями; последние постепенно вытесняют передачи с тангенциальными зубьями.

Рис.14.1

Конические зубчатые колеса с криволинейными зубьями могут иметь круговую, эвольвентную и циклоидальную линию зубьев; наиболее распространенные колеса с круговыми зубьями.

К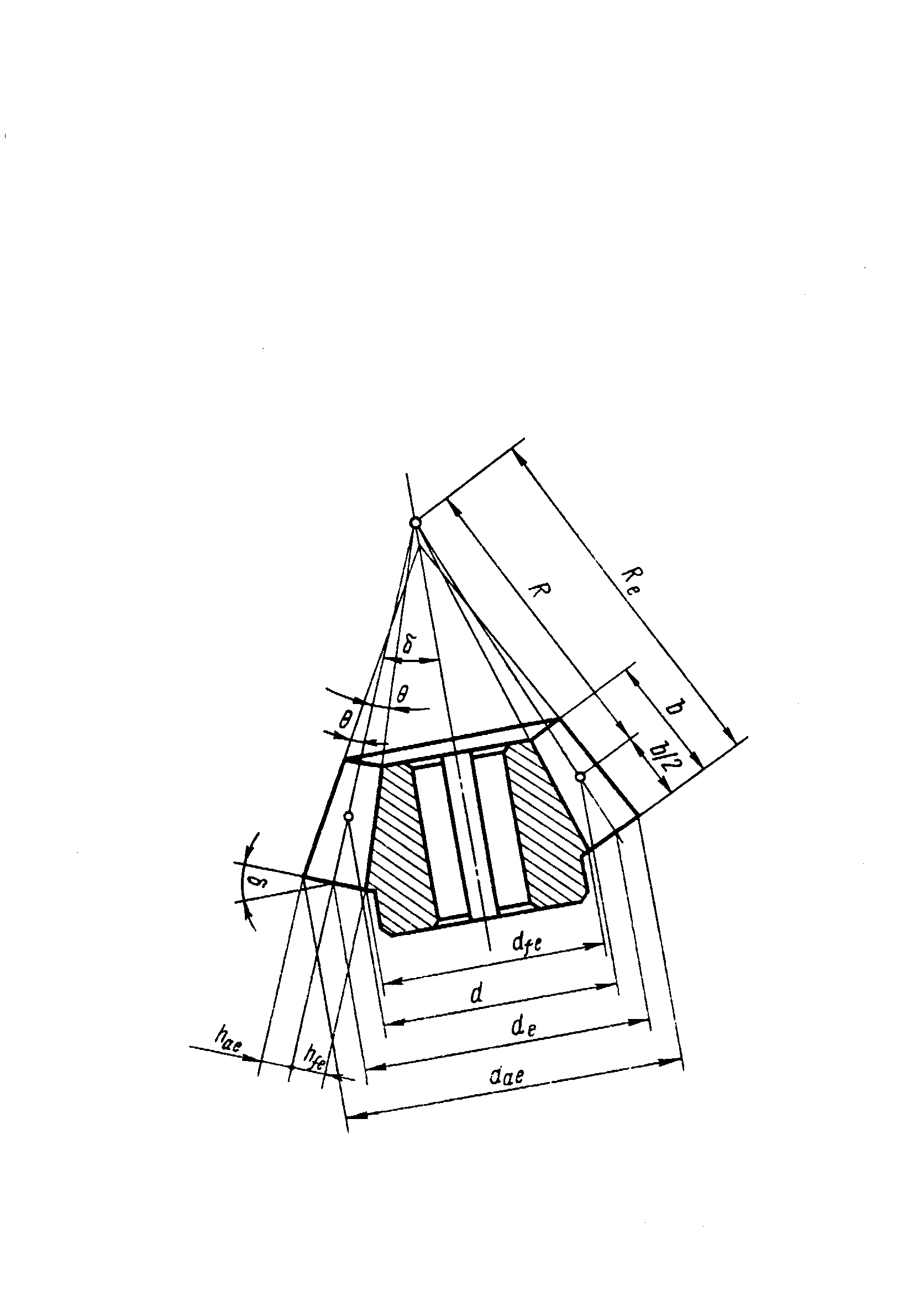 онические передачи с криволинейными зубьями по сравнению с прямозубыми имеют большую нагрузочную способность, работают более плавно, и следовательно, динамические нагрузки и шум при их работе меньше.

Рис.14.2

m – средний делительный окружной модуль;

d = mz – делительный диаметр среднего сечения;

z₁ = 18...30 – число зубьев шестерни;

m_e – внешний делительный окружной модуль;

Сначала конструктор выбирает внешний окружной модуль m_te, из которого рассчитывается вся геометрия зацепления, в частности, нормальный модуль в середине зуба

m_nm= m_te (1 – 0,5 b/R_e),

где: R_e – внешнее конусное расстояние.

Силы в конической передаче действуют аналогично цилиндрической, однако следует помнить, что из-за перпендикулярности осей радиальная сила на шестерне аналогична осевой силе для колеса и наоборот, а окружная сила при переходе от шестерни к колесу только меняет знак

; .

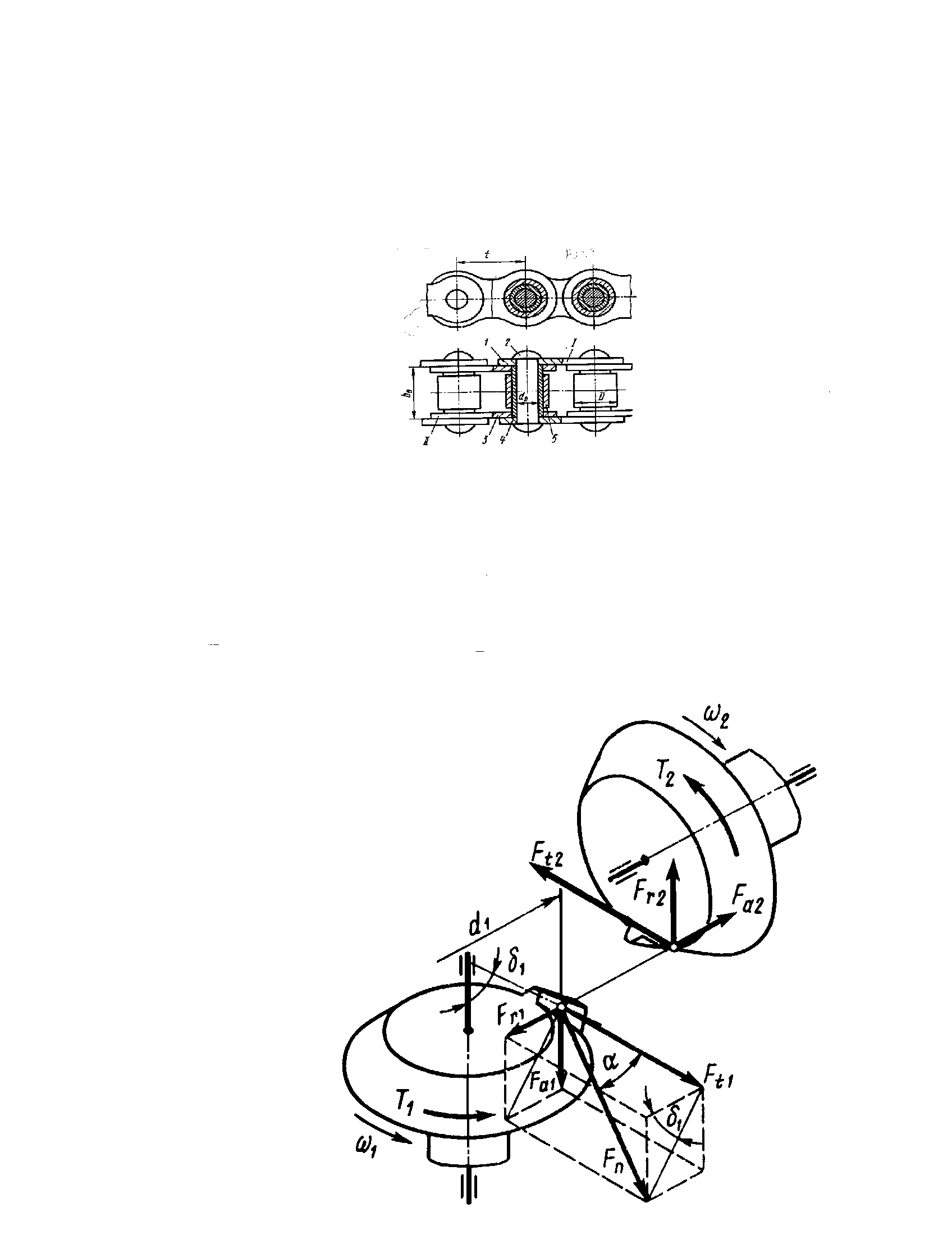
Рис.14.3.

Прочностные расчёты конических колёс проводят аналогично цилиндрическим. Из условия контактной выносливости определяют внешний делительный диаметр d_we, из условия прочности на изгиб находят нормальный модуль в середине зуба m_е. При этом в расчёт принимаются воображаемые эквивалентные колёса с числами зубьев Z_э1,2 =Z_1,2 / cos_1,2 и диаметры d_э1,2 = m_e Z_1,2 / cos_1,2. Здесь Z₁, Z₂, - фактические числа зубьев конических колёс. При этом числа Z_э1,2 могут быть дробными.

В эквивалентных цилиндрических колёсах диаметр начальной окружности и модуль соответствуют среднему сечению конического зуба, вместо межосевого расстояния берётся среднее конусное расстояние, а профили эквивалентных зубьев получают развёрткой дополнительного конуса на плоскость.

14.1. Расчёт закрытой конической зубчатой передачи

Рис.14.4

Наибольшее применение в редукторостроении получили прямозубые конические колёса, у которых оси валов пересекаются под углом S=90° (рис. 14.3).

Проектный расчёт. Основной габаритный размер передачи - делительный диаметр колеса по внешнему торцу - рассчитывают по формуле [1] :

,

где: Епр - приведённый модуль упругости, для стальных колёс Епр =Естали= =2,1×105 МПа;

T2 - вращающий момент на валу колеса, Н×мм;

K_нβ - коэффициент неравномерности распределения нагрузки по длине зуба, определяют по графикам на рис.14.4.

Здесь К_be - коэффициент ширины зубчатого венца относительно внешнего конусного расстояния, .

Рекомендуют принять К_be £ 0,3. Меньшие значения назначают для неприрабатываемых зубчатых колёс, когда H1 и H2 > 350 HB или V > 15 м/с.

Наиболее распространено в редукторостроении значение К_be = 0,285, тогда предыдущее выражение для определения делительного диаметра по внешнему торцу колеса принимает вид

,

где: u_р – расчетное передаточное число конической передачи.

.

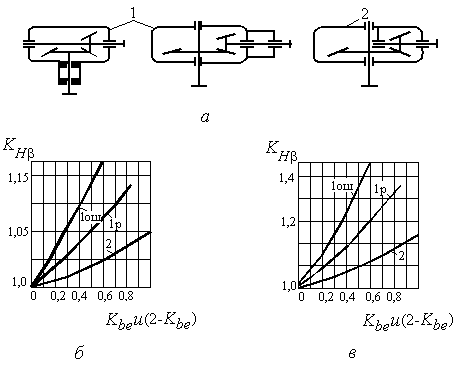
Рис. 14.5

Геометрический расчёт. Определяют диаметр шестерни по внешнему торцу .

Число зубьев шестерни назначают по рекомендациям.

По значению определяют число зубьев шестерни:

при Н1 и Н2 £ 350 HB ,

при Н1 ³ 45 HRC и Н2 £ 350 HB ,

при Н1 и Н2 ³ 45 HRC .

Вычисленное значение z₁ округляют до целого числа.

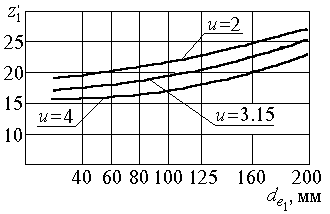
Рис.14.6

Определяют число зубьев колеса .

Вычисленное значение округляют до целого числа. После этого необходимо уточнить:

- передаточное число передачи ,

- угол делительного конуса колеса ,

- угол делительного конуса шестерни ,

- внешний окружной модуль .

Рекомендуется округлить до стандартного значения m_еф по ряду модулей: 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10. После этого уточняют величины диаметров и .

Рассчитывают величину внешнего конусного расстояния передачи .

Рабочая ширина зубчатого венца колеса .

Полученное значение округляют до ближайшего из ряда нормальных линейных размеров.

Определяют расчётный модуль зацепления в среднем сечении зуба

.

При этом найденное значение не округляют!

Рассчитывают внешнюю высоту головки зуба .

Внешнюю высоту ножки зуба определяют как .

Внешний диаметр вершин зубьев колёс рассчитывают по формуле

.

Угол ножки зуба рассчитывают по формуле .

Проверочный расчёт. При расчёте на выносливость зубьев колёс по контактным напряжениям проверяют выполнение условия

,

где: Eпр -приведённый модуль упругости, для стальных колёс Eпр = Eстали = =2,1×105 МПа ;

- вращающий момент на шестерне, Н×мм, ;

здесь - кпд передачи;

- коэффициент расчётной нагрузки, ; коэффициент концентрации нагрузки ;

- коэффициент динамической нагрузки, назначенной по окружной скорости ;

- делительный диаметр шестерни в среднем сечении зуба;

;

- угол зацепления, =20° .

Далее проверяют зубья колёс на выносливость по напряжениям изгиба по формулам:

и ,

где: - окружное усилие в зацеплении, Н, ;

- коэффициент расчётной нагрузки, . Здесь , а - коэффициент динамичности.

- коэффициент формы зуба соответственно шестерни и колеса, находят по таблице в зависимости от эквивалентного числа зубьев колёс

.