Лекция 11

Кинематическое исследование механизмов передач. Передаточные отношения одноступенчатых и многоступенчатых механизмов. Механизмы передач с подвижными осями.

11.1. Механизмы передач с неподвижными осями.

Простейшим является трехзвенный зубчатый механизм, состоящий из стойки и двух зубчатых колес, меньшее из которых называется шестерней. В зацеплении находится высшая кинематическая пара ВКП, а в осях – две низшие вращательные кинематические пары НКП.

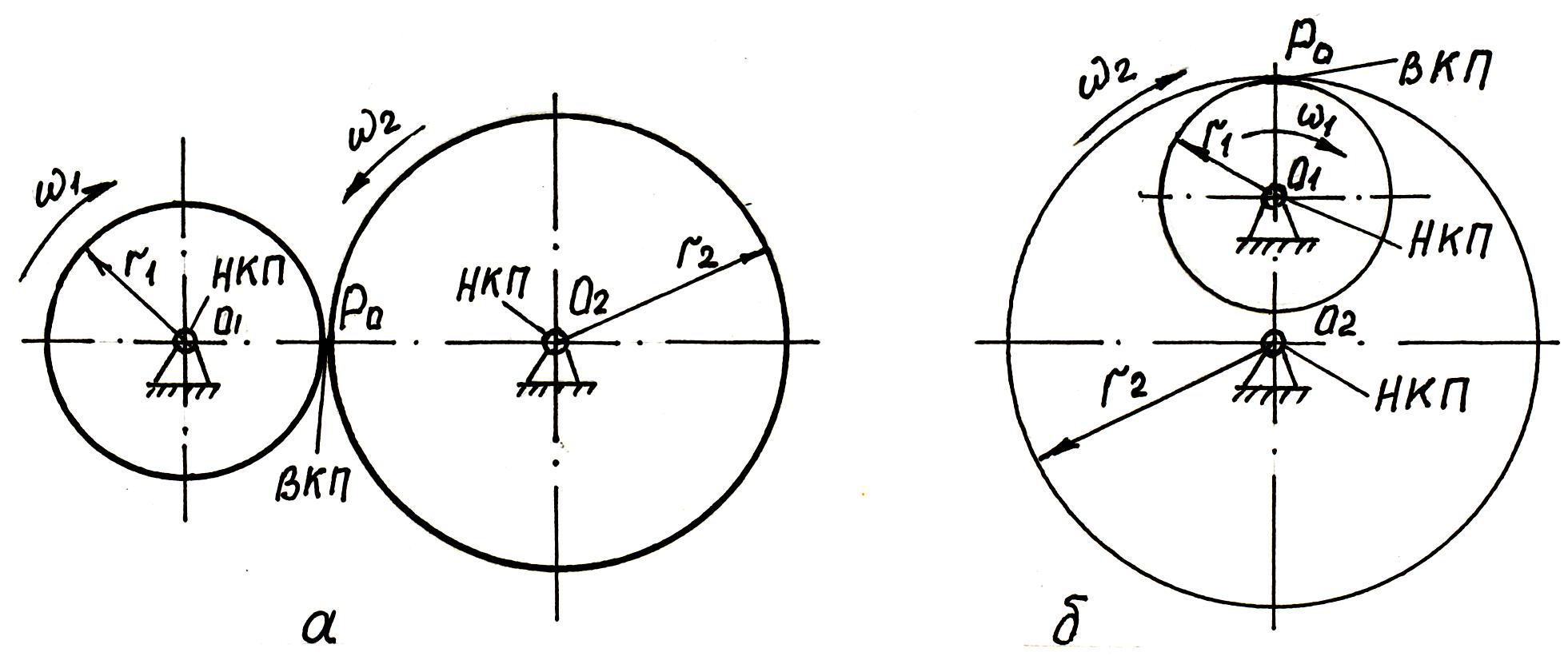
Рис. 11.1

Зубчатый механизм может быть с внешним (рис. 11. 1. а) и внутренним (рис. 11. 1. б) зацеплением. Точка Р₀ представляет собой мгновенный центр вращения в относительном движении зубчатых колес. Радиусы r₁ и r₂ являются радиусами окружностей, перекатывающихся друг по другу без скольжения и называющихся центроидами или начальными окружностями. Как видно из рис. 11.1, при внешнем зацеплении колеса вращаются в противоположные стороны, а при внутреннем зацеплении – в одну сторону.

Отношение угловых скоростей ω₁ и ω₂ двух взаимосвязанных звеньев механизма называется передаточным отношением:

; .

Для зубчатого механизма, у которого угловые скорости всегда обратно пропорциональны количеству зубьев, можно записать:

; .

Знак «плюс» относится к внутреннему зацеплению, при котором угловые скорости ω₁ и ω₂ одного направления; знак «минус» относится к внешнему зацеплению, при котором угловые скорости ω₁ и ω₂ противоположно направлены.

Отношение угловых скоростей ведущего звена ω₁ к ведомому звену ω₂ по модулю называется передаточным отношением:

.

При передача является понижающей и называется редуктором; при передача является повышающей и называется мультипликатором.

Для исследования закона распределения скоростей точек зубчатых колес применяется метод Смирнова, с помощью которого можно графически определить скорость любой точки зубчатого колеса по картине скоростей.

Пусть окружности с радиусами r₁ и r₂ , соприкасаясь в точке Р, перека-тываются без скольжения друг по другу с угловыми скоростями ω₁ и ω₂ (рис. 11.1).

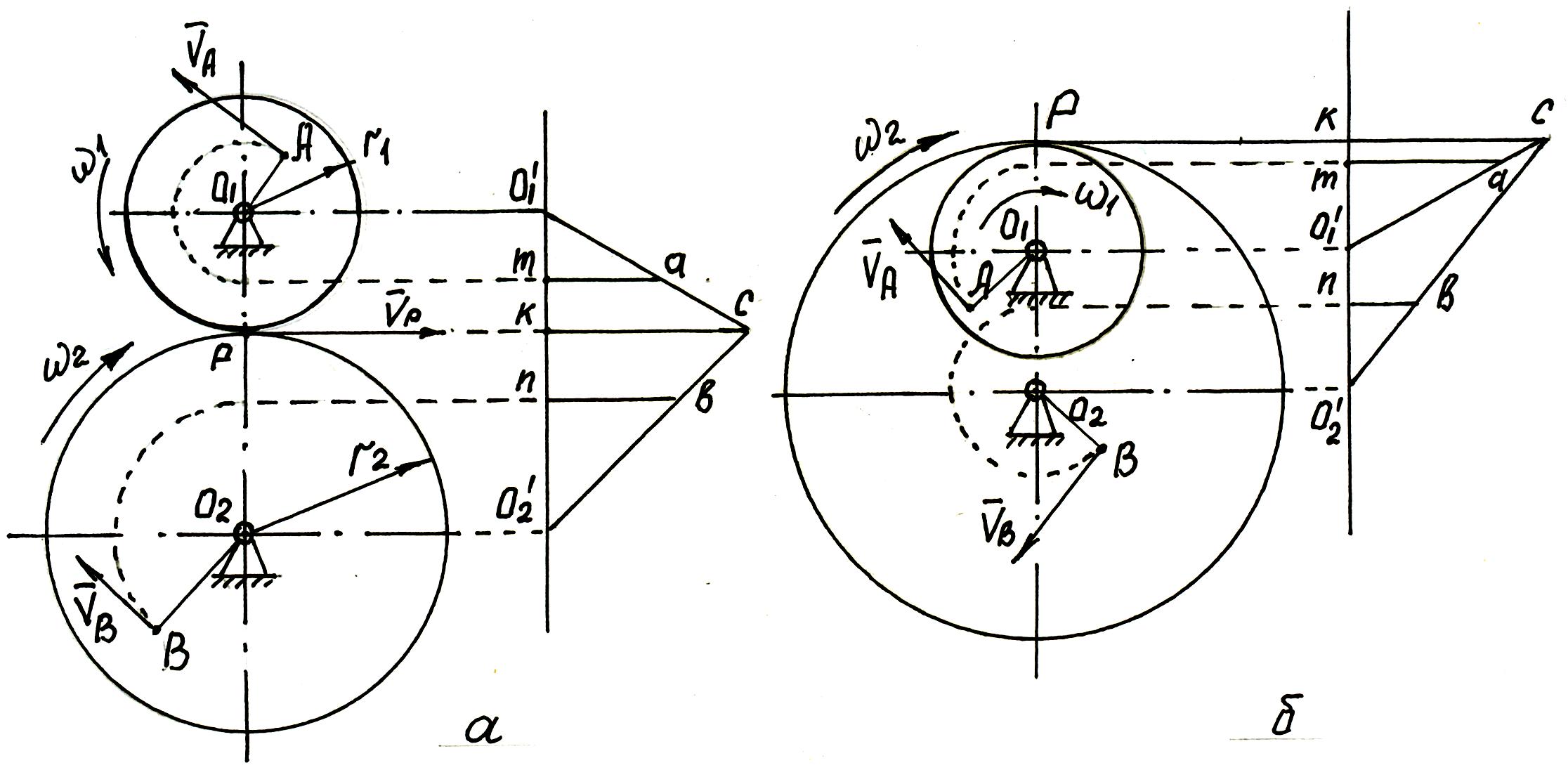
Рис. 11. 2

Проводим прямую параллельно межцентровой линии О₁О₂ и проектируем на нее точки О₁, Р и О₂, в результате получим точки , К и .

Скорости точки Р, принадлежащей обеим окружностям, равны и направлены перпендикулярно межцентровой линии О₁О₂, причем , и . Из точки К откладываем вектор в масштабе в виде отрезка . Так как скорости точек О₁ и О₂ равны нулю, соединяем точки и с точкой С, в результате чего получаем два треугольника и , которые являются картинами распределения скоростей точек зубчатых колес 1 и 2.

При необходимости определения скорости точки А, принадлежащей зубчатому колесу 1, или скорости точки В, принадлежащей колесу 2, необходимо их перенести по направлению угловых скоростей ω₁ и ω₂ на прямую О₁О₂, а затем спроектировать на прямую . Отрезки ma и nb в масштабе определяют скорости точек А и В:

; .

При этом векторы этих скоростей перпендикулярны их радиусам, т.е. , .

Аналогично построена картина распределения скоростей зубчатых колес при внутреннем зацеплении (рис. 11.2.б), по которой точно также определяются скорости точек V_A и V_B.

При наличии в механизме нескольких ступеней зубчатых передач, имеющих передаточные числа и₁, и₂, и₃ и т.д., общее передаточное число и определяется как их произведение: и= и₁·и₂ · и₃ .

Если несколько зубчатых колес непосредственно связаны друг с другом, то все зубчатые колеса, кроме первого и последнего, не оказывают влияние на общее передаточное число и называются паразитками. Они только увели-чивают межцентровое расстояние и изменяют направление вращения.