9.3. Классификация механизмов

Простой механизм, состоящий из одного подвижного звена, образующего с неподвижным звеном низшую кинематическую пару, называется механизмом I класса (рис. 9.4).

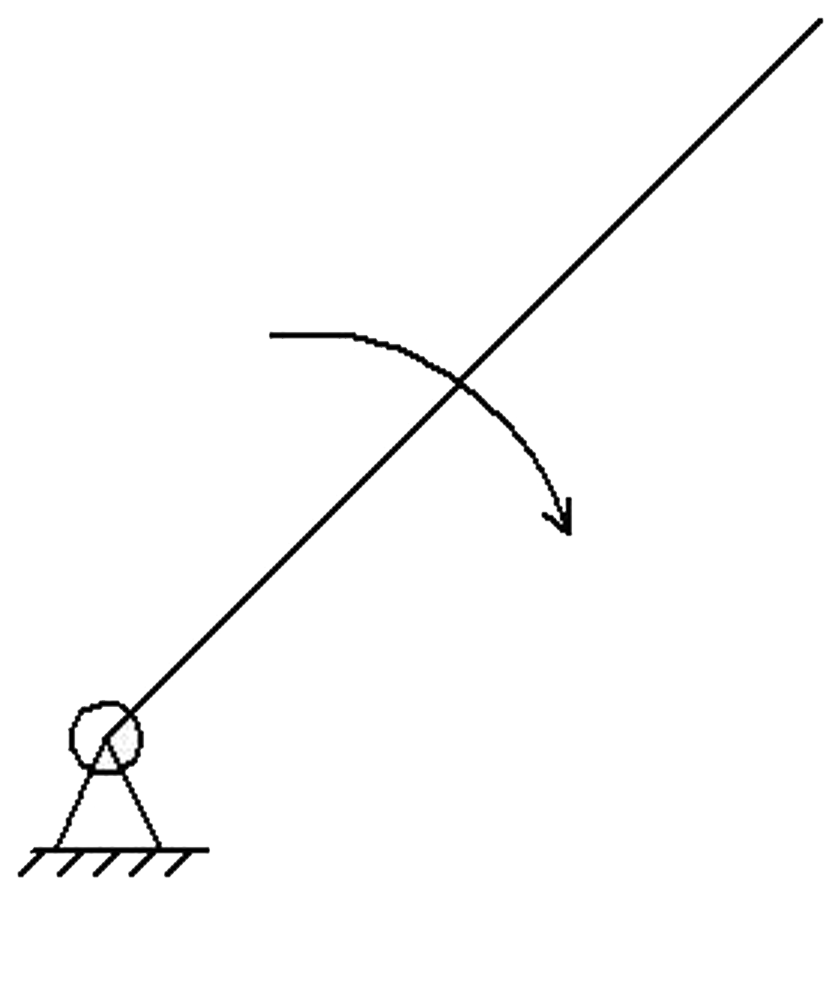
Рис. 9.4

Группой Ассура называется плоская кинематическая цепь, присоединение которой к другой кинематической цепи не изменяет числа степеней свободы последней, т. е. группа Ассура имеет нулевую степень свободы.

Степень подвижности W плоских механизмов определяется по формуле Чебышева W = 3n – 2P₅ – P₄,

где : n – число подвижных звеньев;

Р₅, Р₄ – число кинематических пар 4, 5 классов;

1, 2, 3 – число исключаемых степеней свободы.

Класс группы Ассура определяется числом внутренних кинематических пар, образующих наиболее сложный замкнутый профиль.

Порядок группы Ассура определяется числом внешних кинематических пар, которыми она может быть присоединена к другой кинематической цепи.

Классификация механизмов по группам Ассура возможна, если выполняются следующие три требования:

– число ведущих звеньев равняется числу степеней свободы механизма;

– ведущее звено образует кинематическую пару с неподвижным звеном;

– все кинематические пары относятся к пятому классу.

Звено, находящееся в пространстве и не связанное с другими звеньями, имеет шесть степеней свободы: три поступательные движения вдоль осей oX, oY, oZ и три вращательные движения вокруг этих осей.

Кинематическая пара накладывает ограничения, т.е. связи, на относительное движение звеньев, связанных этой кинематической парой.

Обозначим S - число связей, накладываемых кинематической парой.

При S=6 звенья теряют относительную подвижность в пространстве, а при S=0 исчезает кинематическая пара. Следовательно, для пространственной системы 1≤ S≤5.

Таблица 9.1

	Пространственная система	Плоская система
Число связей кинематической пары S	5 4 3 2 1	2 1
Класс кинематической пары	V IV III II I	II I
Число степеней свободы звена Н	Н=6-S 1 2 3 4 5	Н=3-S 1 2
Подвижность кинематической пары	одно- 2-х 5-ти подв. подв. подв. ……… ..	одно- 2-х подв. подв.

На плоскости свободное звено имеет три степени свободы: два поступательных движения вдоль осей oX, oY и одно вращательное движение вокруг оси, перпендикулярной плоскости XoY . В этом случае число связей, накладываемых кинематической парой на относительное движение связанных звеньев может быть 1≤ S≤2.

Кинематические пары делятся на классы, которые соответствуют числу накладываемых связей (табл.9.1).

Число степеней свободы звена кинематической пары равно разности числа степеней свободы звена, не связанного кинематическими парами, и количества наложенных связей.

Подвижность кинематической пары равна числу степеней свободы звена, связанного этой кинематической парой.

Структурными формами называются закономерности, связывающие число степеней свободы Н кинематической цепи механизма с числом звеньев и числом и видом его кинематических пар.

Для определения числа степеней свободы пространственного механизма применяется структурная формула Сомова-Малышева:

W = 6n-5p₅-4p₄-3p₃-2p₂-p₁ ,

где W – число степеней подвижности;

n – число подвижных звеньев;

p₅ – число кинематических пар 5 класса;

p₄ - число кинематических пар 4 класса;

p₃ - число кинематических пар 3 класса;

p₂ - число кинематических пар 2 класса;

p₁ - число кинематических пар 1 класса.

Эта формула служит для определения степени подвижности пространственной кинематической цени. Пример: карточка.