8.2. Расчет на прочность по нормальным напряжениям

Расчет балок на прочность проводят для опасного сечения – сечения, в котором имеет наибольшее значение. Для балок из пластичных материалов (рис. 46,а), для которых , симметричных относительно нейтральной оси ( ) условие прочности при­мет вид

,

где: – осевой момент сопротивления или момент сопротивления при изгибе. Этот параметр является геометричес­кой характеристикой поперечного сечения балки, определяющей ее прочность при изгибе.

Для хрупких материалов допускаемые напряжения на растяжение и сжатие неодинаковы (например, для чугуна ). Поэтому для таких балок применяют сечения неси­мметричные относительно нейтрального слоя (рис. 46,б). В та­ком случае необходимо нагружать балку так, чтобы , и составлять два условия прочности:

а) по наибольшим растягивающим напряжениям (точка )

;

б) по наибольшим сжимающим напряжениям (точка )

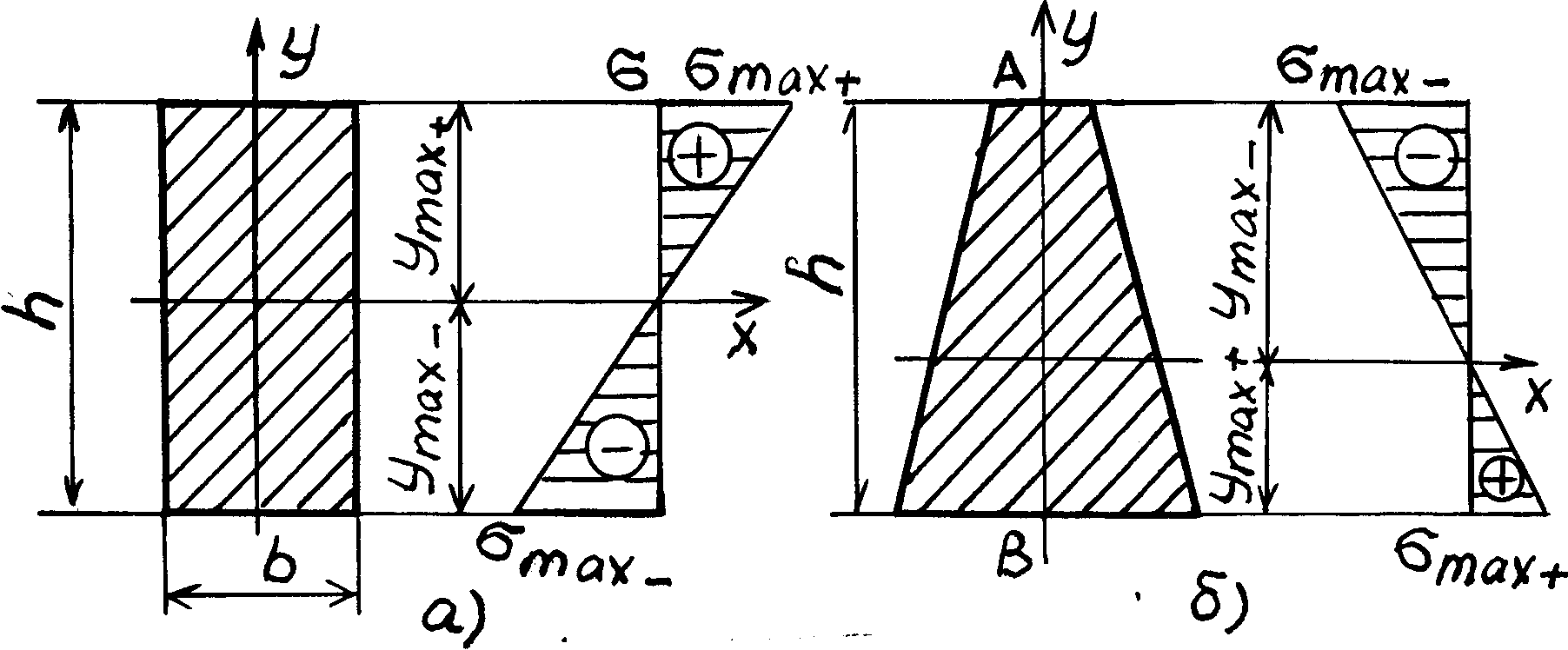
Рис. 8.4

.

Значения для простейших сечений следующие:

Для прямоугольника (рис.8.4, а)

; ;

для круга (рис. 8.4, б)

;

для кольца (рис. 8.4, в)

; ;

или .

Для прокатных профилей (двутавры, швеллеры и др.) и указаны в таблицах сортамента.

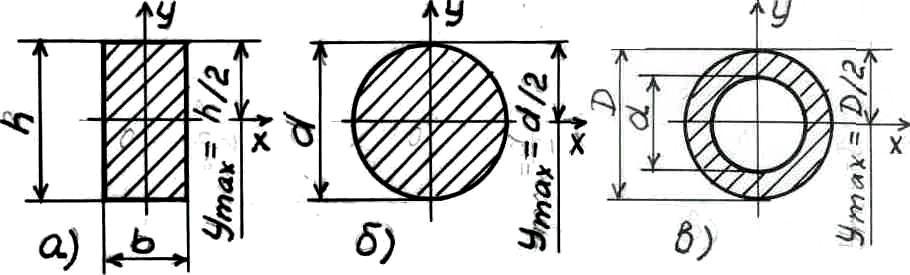
Рис. 8.5

Из условий прочности вытекает три типа за­дач: а) проверочный расчет: зная максимальный изгибающий момент в опасном сечении балки, размеры и форму поперечного сечения, определяющие величину и свойства материала, т.е. , получают для пластичных материалов

.

Для хрупких - используют формулы

,

б) проектировочный расчет: зная и , подбирают поперечное сечение

.

Для хрупких материалов определение размеров поперечного сечения выполняют при заданном соотношении размеров методом приближений, проверяя затем выполнение условий прочности .

в) определение допускаемой нагрузки: для пластич­ных материалов : .

Зная связь между и нагрузкой (по построенной эпюре ), определяют допускаемую внешнюю нагрузку.

Для хрупких материалов определяют наименьший из двух   .

8.3. Рациональные формы сечения балок.

Сечения балок, материал которых одинаково работает на растяжение и сжатие, должны быть прежде всего симмет­ричны относительно нейтральной линии, чтобы .

Н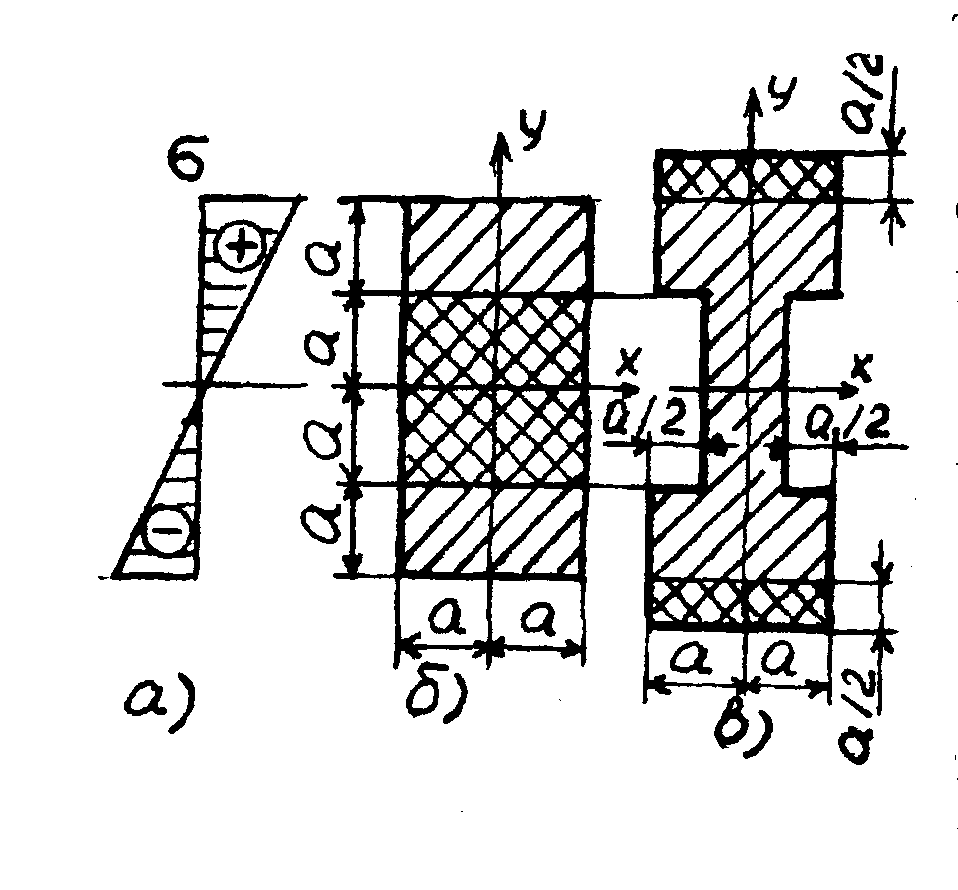 а рис. 8.6,а представлена эпюра , построен­ная по известной формуле (7.6): . Рассмотрим прямо-угольник (рис. 8.6,б).

. 7.13

Найдем часть изгибающего момента , воспринимаемого половиной площади сечения (дважды заштрихована).

Рис.8.6

Для всей площади сече­ния имеет место зависимость:

.

Для половины площади сечения это выражение примет вид: , где - осевой момент инерции половины площади сечения (дважды заштрихованной). Приравняв правые части этих выражений, получим

,

где: ; .

Таким образом, получим, что центральная половина площади поперечного сечения воспринимает , составляющий 1/8 от . Такая форма не является рациональной при изгибе балки.

Изменим форму сечения, сохранив его первоначальную площадь (рис. 8.7,в). Вычислим осевые мо­менты сопротивления до и после изменения формы поперечного се­чения:

; .

Их отношение, = 1,51. Следовательно, вслед­ствие увеличения по сравнению с первоначальным , явив­шегося результатом переноса материала из нейтрального слоя на периферию (т.е. без увеличения веса балки), максимальный изги­бающий момент, который может быть воспринят измененным сечени­ем, возрос в 1,51 раза .

Стремление к рациональному использованию материала балок, привело к созданию прокатных профилей в виде двутавров, швеллеров (рис. 8.7,а,б), клепанных (сварных) металлических и клееных деревянных балок (рис. 8.7,в,г).

Р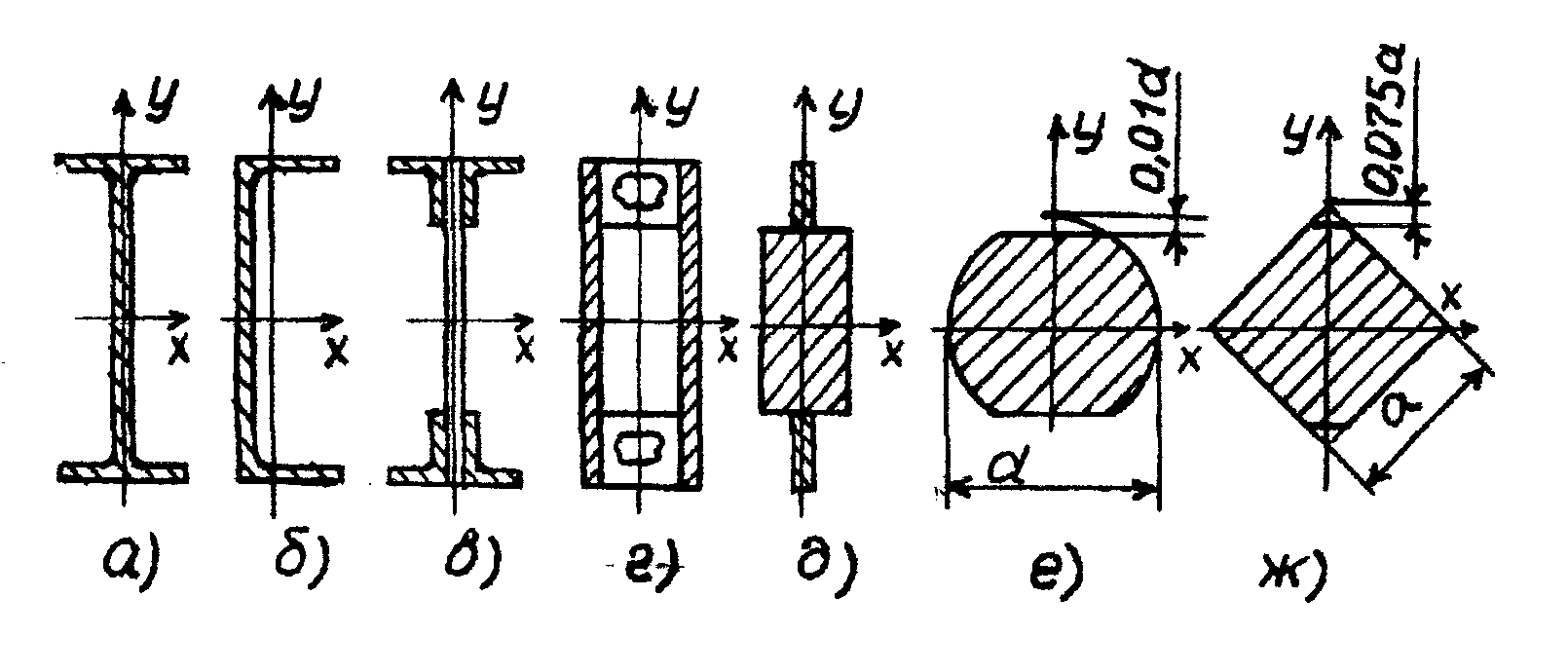 ис 8.7

Возможны исключительные случаи уменьшения прочности балок в результате увеличения площади их поперечных сечений. Например, приварив к прямоугольнику полосы сверху и снизу, получают уменьшение (рис. 49,д). Это происходит за счет того, что степень увеличения при этом меньше степени увеличения . С другой стороны с уменьшением площадей круга и квадрата (рис. 49,е,ж) их мо­менты сопротивления окажутся максимальными.

Рациональность сечений оценивают безразмерным параметром . Сечение при этом считается тем рациональнее, чем больше его . Например, для круга – = 0,141; для кольцевого сечения = 0,294 ( = 0,7); для двутавра №20 – = 1,35.

Балки, материал которых неодинаково работает на растяже­ние и сжатие (хрупкие материалы) и у которых обычно , должны иметь сечения, несимметричные относитель­но нейтральной оси (рис. 8.7, б).

Чтобы балка была равнопрочной в зонах растяжения и сжа­тия, их форма должна удовлетворять условию

,

которое вытекает из условий прочности .

Раздел 3. Теория механизмов и машин

Лекция 9.

Основные понятия. Классификация машин, механизмов, кинематических пар и цепей. Число степеней свободы. Кинематические цепи. Степень подвижности механизмов.

ТММ есть наука, изучающая структуру, кинематику и динамику механизмов в связи с их анализом и синтезом.

Анализ механизмов состоит в исследовании структурных, кинематических и динамических свойств механизма по заданной его схеме.

Синтез механизма – в проектировании схемы механизма по заданным его свойствам.

Кинематика изучает методы определения скоростей, ускорений точек звеньев механизма, а также кинематическое проектирование механизмов по заданным условиям.

Динамика изучает методы определения сил, действующих на элементы механизма и машин в процессе их движения, а также устанавливает взаимосвязь между движением элементов и силами, действующими на них.

Задача изучения курса: научить студентов методам исследования механизмов и машин, умению технически грамотно выполнять расчеты и рационально конструировать детали, сборочные единицы и машины в целом.