3. Определение координат центра изгиба.

Для определения абсциссы центра изгиба предполагаю, что в заданном сечении действует сила , приложенная в центре изгиба. В качестве полюса принимаю начало координат. Тогда система (2) примет следующий вид:

(3)

Коэффициенты при неизвестных уже определены выше, следовательно, система(3) имеет следующее решение:

q₀₁=9,456 кг/см

q₀₂=18,975 кг/см

X_ц.и.=3,968 см

Для определения ординаты центра изгиба предполагаю, что в заданном сечении действует сила , приложенная в центре изгиба, в направлении оси Х. В качестве полюса принимаю начало координат. Тогда система (2) примет следующий вид:

(4)

Где коэффициенты определены выше; а коэффициенты определяю аналогично найденным в пп. 2.2.

Таким образом, система (4) имеет следующее решение:

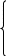
q₀₁=-10,765 кг/см

q₀₂=-20,432 кг/см

Y_ц.и.=4,756 см

Найденное значение ординаты центра изгиба относительно Ц.Т. сечения.

Итак, центр изгиба имеет следующие координаты О(3,968;4,756) .

Расчет тонкостенных консольных балок

Содержание задачи:

1. Определить напряжения в стенках, поясах и стойках.

2. Построить эпюры усилий в поясах и стойках.

Расчетные данные
Р, кг	q, кг/см	δ, см	h, см	, см	, см
700	105	0,2	20	60	60	8	4,0

Материал конструкции: дюралюминий.

Решение

1.Опредение реакций в опорах а и в.

;

;

.

;

;

.

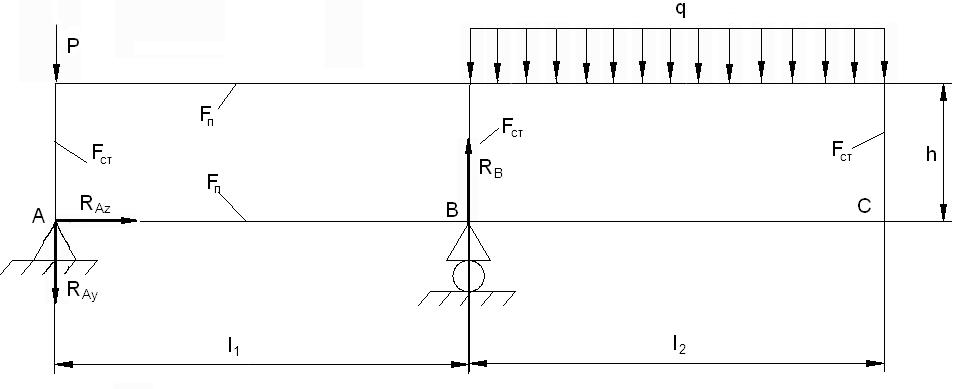
Решая эту систему, получаем:

; ; .

2.Построение эпюр перерезывающих сил и изгибающих моментов.

;

,

,

,

,

,

.

3.Определение напряжений в сечениях балки

Изгибное напряжение в поясах

где М – изгибающий момент в сечении, W – момент сопротивления изгибу сечения.

где – для всех сечений,

– момент инерции сечения,

- момент инерции пояса,

где – площадь сечения пояса.

Момент инерции стойки не учитываем, т. к. он вносит незначительный вклад в работу балки на изгиб.

– момент инерции стенки

Итак, для сечения А:

Для сечения В:

Для сечения С:

Напряжения в стойках равны:

Стойка в сечении А:

Стойка в сечении В:

Стойка в сечении С:

Касательные напряжения в стенках равны:

В сечении А:

В сечении В:

В сечении С:

4.Определение усилий в элементах балки до потери устойчивости

Согласно первой теории для расчета тонкостенных балок внешнюю распределенную нагрузку сводим к двум сосредоточенным силам, действующим в соседних узлах.

Согласно второй теории, до потери устойчивости стенка воспринимает только касательные усилия , постоянные по толщине стенки:

Согласно третьей теории пояса и стойки до потери устойчивости стенки работают только на растяжение или сжатие. Определим усилия в верхних и нижних поясах и в стойках, воспользовавшись уравнениями равновесия статики:

,

,

Отсюда,

,

.

Из условия равновесия для стойки следует следующее выражение:

Для левой стойки:

Для правой стойки:

Для средней стойки:

На основе полученных данных построим эпюры усилий по контуру балки.

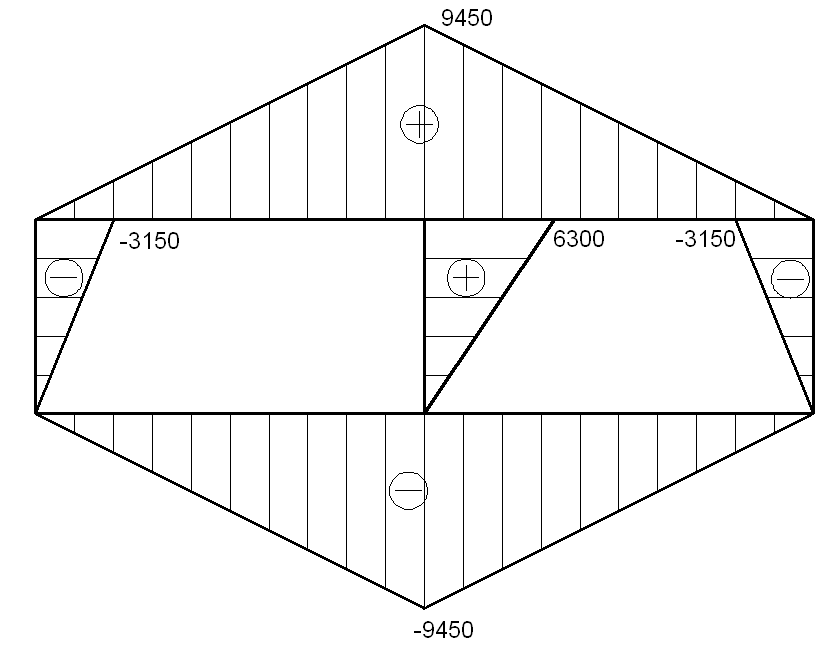
Сравним касательные усилия в стержнях с критическими, для менее устойчивой стенки 1:

где:

Так как , следовательно стенка теряет устойчивость и в ней появляется система косых волн.