
ТЕХНІЧНА МЕХАНІКА РІДИНИ
ТМРГ – є фундамент для засвоєння розрахункових принципів в таких галузях техніки як тепловодопостачання, газопостачання, каналізація, вентиляція. ТМРГ – технічне застосування законів механіки рідини для інженерної практики, а тому вона має додаток технічна. Задачами ТМРГ є вивчення законів та явищ, які спостерігаються в нерухомих та рухомих рідинах і застосування існуючих закономірностей для розрахунків закритих трубопроводів та відкритих русел різного призначення.
Рідина та її властивості
Рідина – це речовина, яка чинить опір стиску і не чинить опір зсуву.
Наслідки:
у зв’язку з відсутністю опору зсуву рідина є рухливим середовищем;
в великих об’ємах рідина не має власної форми, а приймає форму посудини, в яку вона налита;
до рідини, з точки зору суцільного середовища, належать і гази.
У зв’язку з цим рідини розділяють на нестислі (вода, нафта, спирти, розчини лугів, кислот тощо) та стислі рідини (гази: повітря, природний газ, всі існуючі в природі гази).
Суцільним середовищем називається така матеріальна субстанція, для якої характерні такі властивості:
в стані спокою та русі в ній відсутні розриви, тобто спостерігаються суцільні середовища;
в цій субстанції відсутні особливі точки з аномаліями густини;
суцільне середовище може бути нестислим і стислим, але в той же час його поведінку можна записувати математичними залежностями для теорії поля.
Фізичні властивості рідини:
густина – це маса рідини, яка розташована в одиниці об’єму
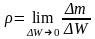 ,
кг/м3
,
кг/м3
Густина рідин коливається в широких інтервалах
 ,
кг/м3;
,
кг/м3;
2) питома вага – це вага одного об’єму рідини
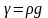 ,
Н/м3;
,
Н/м3;
в’язкість. Між молекулами рідини діють сили протягування, а тому при її русі спостерігається опір рідини викликаний тим, що шари рідини або газу ковзають один від одного і тоді спостерігається таке явище як в’язкість. В’язкість характеризує коефіцієнт кінематичної
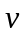 ,
(м3/с)
або коефіцієнт динамічної в’язкості
,
(м3/с)
або коефіцієнт динамічної в’язкості
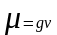 ,
(Па/с);
,
(Па/с);температурне (об’ємне) розширення рідин: при нагріванні тіла розширюються (це для нестислих рідин). Розширення рідин характеризується коефіцієнтом температурного розширення
 ,
(1)
,
(1)
де
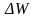 - зміна об’єму, (м3);
- зміна об’єму, (м3);
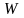 -
початковий об’єм, (м3);
-
початковий об’єм, (м3);
 -
зміна
температури,
-
зміна
температури,
 .
.
Як правило, в довіднику наведені коефіцієнти температурного розширення для найбільш вживаних рідин в залежності від тиску та температури. За цими коефіцієнтами знаходять зміну об’ємів при нагріванні
(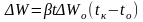
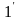 )
)
Приклад. Обчислити об’єм розширювального бачка для системи опалення, якщо tо=5 , tк=95 ,
 =2
м3,
=2
м3,
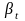 =10-4
1/град.
=10-4
1/град.
Розв’язання
Застосовуємо формулу зміни об’єму

Об’ємне розширення стислих газів характеризується законом Клайперона-Мендєлєєва
 ;
;
стисливість рідин. Рідини практично не стискаються, але при великих навантаженнях вони теж змінюють свій об’єм. Стисливість рідин характеризується коефіцієнтом об’ємного стиску
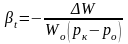 ,
(2)
,
(2)


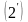
Wк=Wо
-
 W.
W.
Для
води коефіцієнт об’ємного стиску
становить
 1/Па. Величина, обернено-пропорційна
об’ємному стиску, називається модулем
пружності рідини
1/Па. Величина, обернено-пропорційна
об’ємному стиску, називається модулем
пружності рідини
(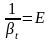 3)
3)
.
Модуль пружності та густина рідини дають змогу обчислити швидкість розповсюдження звуку в рідині (твердих тілах)
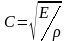 . (4)
. (4)
Швидкість звуку в рідинах дозволяє оцінити інтенсивність гідравлічних ударів в водяних трубопроводах.
Приклад.
Обчислити швидкість звуку у воді, якщо
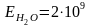 Па,
Па,
 кг/м3.
кг/м3.
Розв’язання
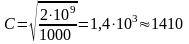 м/с.
м/с.
З
якою швидкістю буде розповсюджуватись
звук в металевій трубі:
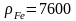 кг/м3,
ЕFe=
кг/м3,
ЕFe=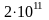 Па.
Па.
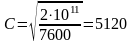 м/с.
м/с.
Сили, що діють в рідині
В рідині можуть діяти нормальні та об’ємні (масові) сили. Нормальні сили – це сили, що діють до по нормалі до поверхні рідини. Це забезпечується контактом рідини зі стінками резервуару або стінками поршня, що діє на рідину, такі нормальні сили називаються силами тиску
P=F/S, (Н/м2=Па)
Дотичні сили до поверхні рідини називаються силами зсуву. Вони виникають тільки при русі рідини

Об’ємні або масові сили – це сили, які діють в об’ємі рідини. Вони зумовлені питомою вагою рідини
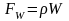
При русі рідини виникають сили інерції, які теж обумовлені питомою вагою рідини або зміною швидкості руху рідини
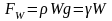

Гідростатика
Гідростатичним тиском в точці називається напруга стискання, що викликано результативною силою, яка діє на поверхню елементарної сфери, що оточує цю точку
 ,
(Н/м2=Па)
,
(Н/м2=Па)
Сили, які діють в рідині. Властивості гідростатичного тиску
1. В нерухомій рідині в кожній точці тиск однаковий на всіх координатних вісях.
2. Гідростатичний тиск завжди діє по нормалях до поверхонь, які обмежують рідину або розташований в рідині і завжди стискає її.
3. Гідростатичний тиск є функцією від координати точки.
P(A)=f(xA,yA,zA)
PA=PA=PA
Умови непорушності рідини. Рівняння Ейлера
Ейлер розглянув непорушний паралелепіпед зі сторонами довжин dx, dy, dz, дослідив сили, що діють на нього і отримав диференційне рівняння.
Ox[X] =[м/с2], Oy[Y]= [м/с2], Oz[Z]= [м/с2]
Умова непорушності по Оу:
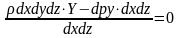
Після скорочення можна отримати наступне диференційне рівняння Ейлера
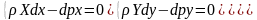 (а),(b),(с)
(а),(b),(с)
Ця система переходить в рівняння повних диференціалів
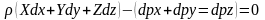
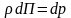
Висновок за Ейлером.
Масові сили по осях напруженість [X,Y,Z]=[м/с2]. Ця напруженість викликана силовим полем, яке має потенціал. Рідина знаходиться в нерухомому стані, якщо масові сили мають потенціал. Якщо потенціал дорівнює 0 або const, то це є поверхні в рідині, де тиск є стало. Величиною. Отже, рівняння поверхонь зі сталим тиском отримаємо на основі диференціального рівняння:
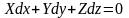

Основне рівняння гідростатики
В полі сил земного тяжіння на горизонтальних поверхнях X=0, Y=0, Z= -g. Використаємо рівняння Ейлера (c)
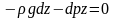
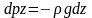

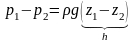
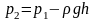 - це
основне рівняння гідростатики (1)
- це
основне рівняння гідростатики (1)
Абсолютний манометричний та вакуумний тиск
Абсолютний тиск – це тиск з урахуванням тиску атмосферного повітря
Раб=Ра+Р (2)
В свою чергу 2-й доданок тиску може називатися манометричним або вакуумним тиском:
1)
якщо Р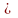 Раб-Ра,
то це манометричний тиск (Рм);
Раб-Ра,
то це манометричний тиск (Рм);
2) якщо Р Раб-Ра, то це вакуумний тиск (РB).
Напір та його різновиди

В основному рівнянні гідростатики:
 ,
,
де
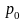 -
зовнішній тиск;
-
зовнішній тиск;
 - ваговий
тиск, обумовлений стовпом рідини висотою
h.
- ваговий
тиск, обумовлений стовпом рідини висотою
h.
Інколи замість тиску дають значення напору, особливо для водяних мереж. В загальному випадку напором називається відношення тиску до питомої ваги рідини

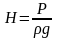 (3)
(3)
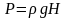
В залежності від того, який має тиск входить у формулу (3), напір (Н) має наступні назви:
1) манометрична висота або п’єзометра hp;
2) п’єзометричний напір На;
3) повний напір Нп.
Відношення манометричного тиску до питомої ваги рідини називається п’єзометрою або п’єзометрична висота hp. Площа, яка проходить через п’єзометричну трубку називається п’єзометричною площиною.
ОО – площа відліку, яка може змінювати своє положення в просторі;
ZA - глибина занурення точки в рідину; ZA геод – відстань від точки А до площі ОО.
На основі малюнку можна записати:
- для точки А
hp+ZA+ ZA геод=Hп
- для точки В
hp+ZВ+ ZВ геод=Hп.
В напорах основне рівняння гідростатики має вигляд
hp+Zі+ =Hп (4)
=Hп (4)
В тисках основне рівняння гідростатики має такий вигляд
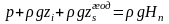 .
.
Закон Паскаля
Основне рівняння гідростатики для 2-х точок


 ,
,

Зовнішній тиск в усі точки рідини передається однаково.
Застосування рівняння гідростатики для практичних потреб
Газовий стояк та димова труба по відношенню з атмосферою мають меншу густину газу. У зв’язку з цим при підйомі по газовому стовпчику тиск у них зміниться не однаково. Для газового стояка
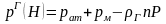

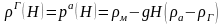

Сила тиску, що діє на плоску стінку
Якщо в рідині виділити плоску стінку, яка може бути стінкою резервуару, стінкою дамби або плотини, то на неї діє сила тиску, ця сила обчислюється за формулою
 де
-
сила тиску в точці О, яка являє собою
центр маси плоскої стінки.
де
-
сила тиску в точці О, яка являє собою
центр маси плоскої стінки.
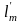 -
апліката
(Zк)
центра мас від урізу рідини;
-
апліката
(Zк)
центра мас від урізу рідини;
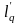 -
апліката центру тиску від урізу рідини.
-
апліката центру тиску від урізу рідини.
Рівнодійна сили тиску буде проходити через точку С, яка називається центром тиску.
В загальному вигляді апліката обчислюється
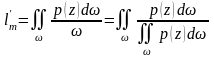


Для практичних розв’язків використовують довідкові дані Агроскіна. Для регулюючих щитів різної форми, їх верхній край, співпадає з урізом води.
B
B
Форма щита |
L |
L |
|
|
Глибина занурення центра мас lm |
L/2 |
L/3 |
D/2 |
4D/6П |
Глибина занурення центра тиску lq |
2L/3 |
L/2 |
5D/8 |
3ПD/32 |
|
BL |
0,5BL |
Пd2/4 |
0,392d2 |
Дані таблиці використовують для розрахунків, коли щити будуть занурені в рідину і центр тиску та центр мас будуть мати інші значення. Нехай відстань від урізу води до верхнього краю щита або стінки буде дорівнювати hp. В такому випадку

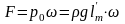

В тому випадку, коли hp має велике значення, тоді


Якщо регулюючий щит розташований в тілі площини на значній глибині, то центр мас співпадає з центром тиску і щит автоматично не відкривається. Необхідність автономного приводу для відкриття щитів під час повені.
Приклад. Обчислити силу, що діє на прямий щит з розмірами: В=5м, L=3м, якщо верхній край щита занурений на глибину hp=4м у воду, кг/м3. F-?, -?
Розв’язання
 м
м
 кн.
кн.
 м
м
Сила тиску, що діє на криволінійні поверхні
Нехай рідина обмежена криволінійною поверхнею. В такому випадку, ваговий тиск створює рідини, яка на криволінійні стінки, що обмежують рідину. В свою чергу стінка за 3-м законом Ньютона створює опір витіканню рідина і рідина стискається.
Рівнодійна сила
 ,
,
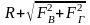

FГ проектується на вертикальну стінку ВД і вона є силою, що діє на плоску стінку.
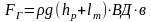
Вертикальна сила FВ буде дорівнювати вазі рідини, що розташована над криволінійною поверхнею
 ,
,
де VТ.Т - об’єм тіла тиску.
Результативна сила R буде нормальною до криволінійної поверхні і вона буде колінеарна або проходитиме з вектором, що проходе через центр тиску С перпендикулярно до криволінійної поверхні.






 ,
м2
,
м2