24. Биноминальное распределение

Биномиальное распределение — дискретное распределение вероятностей случайной величины принимающей целочисленные значения с вероятностями:

Основные свойства:

Характеристическая функция:

Моменты:

• Математическое ожидание:

• Дисперсия:

• Асимметрия: 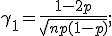при распределение симметрично относительно центра

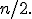
Асимптотические приближения при больших

Если значения велики, то непосредственное вычисление вероятностей событий, связанных с данной случайной величиной, технически затруднительно. В этих случаях можно использовать приближения биномиального распределения распределением Пуассона и нормальным (приближение Муавра-Лапласа).

25. Равномерное распределение случайной величины.

Непрерывная случайная величина Х равномерно распределена в интервале [а; в], если ее плотность вероятности в этом интервале постоянна, т.е. если все значения в этом интервале равновероятны:

Значение постоянной с определяется из условия нормировки:

.

Функция распределения:

,

Числовые характеристики равномерно распределенной случайной величины определяются так:

 

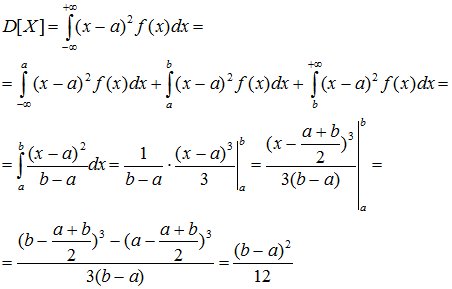
Среднее квадратичное отклонение равномерного распределения равно

Равномерное распределение случайной величины полностью определяется двумя параметрами: a и b – интервалом, на котором определена случайная величина.

При необходимости можно определить параметры a и b равномерного распределения по известным значениям математического ожидания m_X и дисперсии D_X случайной величины. Для этого составляется система уравнений следующего вида:

,

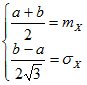из которой определяются искомые параметры.

Вероятность попадания равномерно распределенной случайной величины в интервал [α,β) определяется так:

, где

26. Нормальный закон распределения (или распределение Гаусса) задается следующей дифференциальной функцией

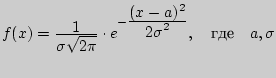 - параметры.

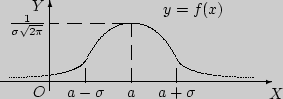
Рис. 56

 (  - max

 = а -  , x  = а +   - точки перегиба.

При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.

            Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:

Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа 

Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.

Это правило называется правилом трех сигм.

На практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.

3 сигма — вероятность попадания очередного фактического значения в доверительный интервал составят 99,7%, или 300 к 1, или существует 0,3% вероятности выхода за границы. Мы сформулировали правило 3 сигм, которое гласит, что вероятность попадания очередного случайного значения в доверительный интервал с заданным значением три сигма составляет 99.7%.

27. Система случайных величин. Свойства функции распределения и плотности

В зависимости от типа, входящих в систему случайных величин, системы могут быть дискретными, непрерывными или смешанными, если в систему входят различные типы случайных величин.

Более подробно рассмотрим системы двух случайных величин.

Определение. Законом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях.

Определение. Функцией распределения системы двух случайных величин называется функция двух аргументов F(x, y), равная вероятности совместного выполнения двух неравенств X<x, Y<y. Свойства функции распределения

1. Значения функции распределения принадлежат отрезку :

2.  —неубывающая функция, т.е. , если

3. Если возможные значения непрерывной случайной величины принадлежат интервалу , то: , если ; , если .

Свойства плотности распределения вероятностей

1. Плотность распределения вероятностей – неотрицательная функция: . 2. Несобственный интеграл от плотности распределения вероятностей в пределах от до равен единице: .

Вероятностный смысл плотности распределения вероятности. Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу , приближенно равна (с точностью до бесконечно малых высшего порядка относительно ) произведению плотности распределения вероятности в точке на длину интервала : .

28. Корреляционным моментом µ_xy случайных величин X и У называют математическое ожидание произведения отклонений этих величин:

µ_xy = M { [ X - M(X) ] [ Y - M(Y) ] }

Для нахождения корреляционного момента дискретных величин используют формулу:

 ,

а для непрерывных величин — формулу :

Корреляционный момент характеризует наличие (отсутствие) связи между величинами X и У. Ниже будет доказано, что корреляционный момент равен нулю, если X и У независимы; Если же корреляционный момент для случайных величин X и Y не равен нулю, то между ними имеется завимость.

Теорема 1.  Корреляционный момент двух независимых случайных величин X и Y равен нулю.

Теорема 2.  Абсолютная величина корреляционного момента двух случайных величин X и Y не превышает среднего геометрического их дисперсий:

Теорема 3.  Абсолютная величина коэффициента корреляции не превышает единицы: