7. Условная вероятность

Если при вычислении вероятности события никаких других ограничений, кроме условий эксперимента, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события В при дополнительном условии, что произошло событие А.

Условной вероятностью   (два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.

Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.

.

В частности, отсюда получаем  .

8. Формула полной вероятности

Пусть имеется группа событий H₁, H₂,..., H_n, обладающая следую­щими свойствами:

1) все события попарно несовместны: H_i 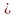H_j =; i, j=1,2,...,n; ij;

2) их объединение образует пространство элементарных исходов :

 =  .

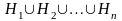Рис.8

В этом случае будем говорить, что H₁, H₂,...,H_n образуют полную группу событий. Такие события иногда называют гипотезами. Пусть А – некоторое событие: А   (диаграмма Венна представлена на рисунке 8). Тогда имеет место формула полной вероятности:

P(A) = P(A/ H₁)P(H₁) + P(A/ H₂)P(H₂) + ...+ P(A/ H_n)P(H_n) =

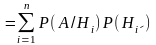
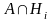Доказательство. Очевидно: A = , причем все события (i = 1,2,...,n) попарно несовместны. Отсюда по теореме сложения вероятностей получаем

P(A) = P(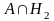 ) + P( ) +...+ P(

Если учесть, что по теореме умножения P( ) = P(A/H_i)P(H_i) (i = 1,2,...,n), то из последней формулы легко получить приведенную выше формулу полной вероятности.

9. Формула Байеса

Пусть событие   происходит одновременно с одним из   несовместных событий  . Требуется найти вероятность события  , если известно, что событие   произошло.

На основании теоремы о вероятности произведения двух событий можно написать

Откуда

или

10. Испытания Бернулли. Наиболее вероятное число успехов

независимые испытания с двумя исходами каждое ("успехом" и "неудачей") и такие, что вероятности исходов не изменяются от испытания к испытанию. Б. и. служат одной из основных схем, рассматриваемых в теории вероятностей.

Пусть р - вероятность успеха и   - вероятность неудачи, и пусть 1 обозначает наступление успеха, а 0 - наступление неудачи. Тогда вероятность определенного чередования успехов и неудач, напр.,

равна

где   - число успехов в рассматриваемом ряду писпытаний. Со схемой Б. и. связаны многие распространенные распределения вероятностей. Пусть  - случайная величина, равная числу успехов в пБ. и. Тогда вероятность события   равна 

т. е.   имеет биномиальное распределение.

11. Локальная теорема Муавра — Лапласа. Если в схеме Бернулли число n велико,а число p отлично от 0 и 1, тогда:

Функция φ(x) называется функцией Гаусса. Ее значения давно вычислены и занесены в таблицу, которой можно пользоваться даже на контрольных работах и экзаменах.