Вопросы и задания для самопроверки.

1. Что такое обратная функция? Приведите примеры.

2. Укажите условия, при которых существует обратная функция.

3. Совпадают ли графики функций , ?

4. Как построить график обратной функции , если известен график функции ?

5. Укажите область определения и область изменения обратной функции , если исходная функция определена на множестве Х, а Y– множество ее значений?

6. Может ли не строго монотонная функция иметь обратную функцию?

7. Обязательно ли функция является строго монотонной, если она имеет обратную?

8. Может ли функция иметь обратную, если функция f(x) имеет обратную, а функция g(x) – не имеет? Приведите примеры.

9. Может ли функция f(x)+g(x) иметь обратную, если функции f(x) и g(x) не имеют обратной функции? Приведите примеры.

Упражнения.

1. Для функции найти обратную функцию, построить график, указать область ее определения.

Р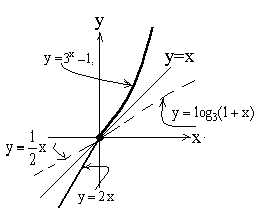 ешение. Так как данная функция строго возрастает на числовой оси, то она имеет обратную функцию. Найдем ее. Если , причем, значения функции образуют бесконечный промежуток . Очевидно, . Значит, – «часть» обратной функции для , областью определения которой является множество , а множество значений – также промежуток . Таким образом, мы построили «часть» обратной функции. Пусть теперь , тогда . Находим из последнего уравнения х: . Следовательно, функция – еще одна «часть» обратной функции (или правильнее сказать еще одно ее сужение), причем, Объединяя полученные формулы в одну, получим обратную к исходной функции: . Ее график изображен на рисунке пунктирной линией .. Он получен путем зеркального отображения исходной функции (симметрии) относительно прямой .

2. Для указанных ниже функций найти обратные функции и построить эскизы их графиков:

1. 2. 3.

4. 5. 6.

7. 8. 9.

10. 11. 12.

13. 14.

15. 16. 17.

18. 19. 20.

Настоящий ученик умеет выводить известное из неизвестного и этим приближается к учителю.

Гете И.

§6.8. Сложная функция.

Пусть функция определена на множестве Х, причем все ее значения образуют множество Y. Предположим, что на множестве Y задана другая функция . Тогда имеет смысл выражение . В самом деле, каждому значению переменной х из множества Х соответствует единственное значение переменной y, которое вычисляется по формуле и принадлежит множеству Y. Так как функция определена на множестве Y, то в точке можно вычислить ее значение по формуле . Выражение называется сложной функцией или суперпозицией (или композицией) (от) двух функций f и g. Переменная у называется промежуточным аргументом функции z. В конечном счете, функция зависит от аргумента х, который изменяется на множестве Х.

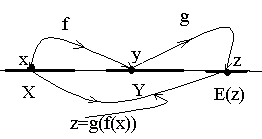
Функция f отображает точку х в точку y, а функция g отображает точку у в точку z.

Аналогично вводится понятие композиции (сложной функции) трех и более функций.

Так, функцию можно рассматривать как сложную функцию от двух функций, положив . Очевидно, эта функция определена для любого х. Функцию можно рассматривать как сложную функцию, образованную тремя функциями . Здесь функция у определена на всей числовой прямой R, функция z определена для , поэтому сложная функция определена лишь для тех х, для которых , т.е. областью определения сложной функции является множество . Заметим, что одну и ту же функцию можно рассматривать как сложную функцию различного числа составляющих ее функций. Например, функцию можно рассматривать как композицию двух функций или как композицию трех функций .

Рассмотрим функции и составим из них сложные функции g[f(x)], f[g(x)], f[f(x)], g[g(x)]. Функция – сложная функция от двух функций и функции . Функция определена на множестве – множество ее значений. Так как функция не определена в точке , то из рассмотрения нужно выбросить точку , в которой . Во всех остальных точках (на множестве ) сложная функция существует и ее значения вычисляются по формуле Сложная функция z=f[g(x)] образована из функции и функции , которая определена для всех . Так как функция определена для ,то ее значения вычисляются по формуле

Функция , где . Значит, . Далее , где . Здесь

Вопросы для самопроверки и упражнения.

1. Что называется сложной функцией? Приведите примеры.

2. При каких условиях на исходные функции существует сложная функция?

3. Совпадает ли сложная функция f[g(x)] с функцией g[f(x)]? Приведите примеры.

4. Укажите условия, при которых существуют сложные функции g[f(x)], f[g(x)], f[f(x)], g[g(x)] и найдите их, если:

N	f(x)	g(x)
	x
	x

5. Для функций составить сложную функцию f{g[h(x)]}.

Понятие функции такое же основное и первоначальное, как и понятие множества.

Ф. Хаусдорф.