
- •Основные символы
- •§6.1. Множества.
- •5. Открытые полупрямые
- •Вопросы и задания для самопроверки.
- •Упражнения.
- •6. Изобразить на координатной плоскости множества:
- •§6.2. Операции над множествами.
- •Вопросы для самопроверки.
- •Упражнения.
- •§6.3. Модуль числа.
- •Вопросы для самопроверки.
- •Упражнения.
- •2. Решить уравнения:
- •Решить неравенства и изобразить решения на числовой оси:
- •Изобразить на координатной плоскости множества точек, координаты которых удовлетворяют следующим соотношениям:
- •§6.4. Границы числовых множеств.
- •Вопросы и задания для самопроверки.
- •Упражнения.
- •§6.5. Открытые и замкнутые множества.
- •Объединение любого семейства открытых множеств есть открытое множество;
- •Пересечение любого конечного семейства открытых множеств есть открытое множество.
- •Объединение конечного числа замкнутых множеств есть замкнутое множество;
- •Пересечение любого семейства замкнутых множеств есть замкнутое множество
- •Вопросы и задания для самопроверки.
- •Упражнения.
- •§6.6. Первоначальные сведения о функциях.
- •1.Понятие функции.
- •2.Четные и нечетные функции.
- •Если то и , т.Е. Область определения функции f является симметричной относительно начала отсчета о;
- •3.Периодические функции.
- •4.Монотонные функции.
- •Вопросы и задания для самопроверки.
- •§6.7. Обратная функция.
- •Вопросы и задания для самопроверки.
- •Упражнения.
- •Для указанных ниже функций найти обратные функции и построить эскизы их графиков:
- •§6.8. Сложная функция.
- •§6.9. Элементарные функции.
- •Основные формулы для степенных функций.
- •Основные формулы для показательной функции.
- •Логарифмическая функция
- •Основные формулы для логарифмической функции
- •Тригонометрические и обратные тригонометрические функции.
- •Основные значения
- •Основные тригонометрические формулы. Формулы сложения
- •Вопросы и задания для самопроверки.
- •§6.10. Метод математической индукции. Нематематическая индукция играет существенную роль в математическом исследовании.
- •Вопросы и задания для самопроверки.
- •Упражнения.
4.Монотонные функции.
Функция
заданная на множестве Х,
называется:
возрастающей, если для
любых
![]() и
и
![]() из Х, таких, что
<
,
выполняется неравенство
из Х, таких, что
<
,
выполняется неравенство
![]() ,неубывающей, если для любых
и
из Х, таких, что
<
,
выполняется неравенство
,неубывающей, если для любых
и
из Х, таких, что
<
,
выполняется неравенство
![]() ,убывающей, если для любых
и
из Х, таких, что
<
,
выполняется неравенство
,убывающей, если для любых
и
из Х, таких, что
<
,
выполняется неравенство
![]() ,невозрастающей,
если для любых
и
из Х, таких, что
<
,
выполняется неравенство
,невозрастающей,
если для любых
и
из Х, таких, что
<
,
выполняется неравенство
![]() .
.
Заметим, что неубывающая и невозрастающая функции могут принимать в различных точках равные значения. (см. рис. 23 и 25).
Возрастающая функция характеризуется тем, что из любых двух точек на графике правая лежит выше левой, т.е. при движении слева направо график функции поднимается (см. рис. 22). Если же функция убывающая, то ее график при движении слева направо график функции опускается (см. рис. 24). Для неубывающей функции график не опускается (рис. 23), для невозрастающей – не поднимается (рис. 25).
Функции,
удовлетворяющие любому из указанных
выше условий, называются монотонными.
При этом возрастающие и убывающие
функции называются строго
монотонными
(или
монотонными в «строгом смысле»),
а неубывающие и невозрастающие функции
называются монотонными
«в широком смысле».ункция
называется кусочно-монотонной,
если область ее определения можно
разбить на «части», на которых она
монотонна. Так,
функция является кусочно-монотонной
на R.
В самом деле, множество R
разобъем на две
![]() является кусочно-монотонной на R.
В самом деле, множество R
разобъем на две
является кусочно-монотонной на R.
В самом деле, множество R
разобъем на две
«части»
![]() ,
,
![]() .
На промежутке
функция убывает, а на промежутке
возрастает. Функции
.
На промежутке
функция убывает, а на промежутке
возрастает. Функции
![]() также являются кусочно-монотонными на
R.
также являются кусочно-монотонными на
R.
Вопросы и задания для самопроверки.
Приведите определение функции, области определения и области изменения функции.
Определяет ли формула
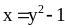 переменную х как функцию переменной
у? Найдите
переменную х как функцию переменной
у? Найдите
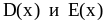 .
Постройте график данной функции.
.
Постройте график данной функции.Определяет ли формула
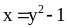 переменную у как функцию переменной
х?
переменную у как функцию переменной
х?При каких условиях формула определяет функцию
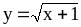 ?
Функцию
?
Функцию
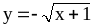 ?
Постройте графики этих функций.
?
Постройте графики этих функций.Приведите определение четной и нечетной функций.
Можно ли всякую функцию представить в виде суммы четной и нечетной функций?
Может ли быть четной (нечетной) сумма, разность, произведение и частное четной и нечетной функций? Приведите примеры.
Приведите определение периодической функции.
Всегда ли сумма (разность) двух периодических функций является периодической функцией?
При каких условиях сумма (разность) двух периодических функций является периодической функцией?
Является ли произведение двух периодических функций периодической функцией? Приведите примеры.
Приведите определения возрастающей, неубывающей, убывающей, невозрастающей функций. Приведите примеры.
Всегда ли сумма двух возрастающих (убывающих) функций является возрастающей (убывающей) функцией? Приведите примеры.
Что можно сказать о характере монотонности суммы убывающей и возрастающей функций? Приведите примеры.
Что можно сказать о характере монотонности произведения (частного) двух монотонных функций? Приведите примеры.
Найдите область определения функций:
1.
![]() 2.
2.
![]() 3.
3.
![]()
4.
![]() 5.
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]() , 9.
, 9.
![]()
10.
![]() 11.
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]() 15.
15.
![]()
16.
![]() 17.
17.
![]() 18.
18.
![]()
19.
![]() 20.
20.
![]() 21.
21.
![]()
Исследовать на четность функции:
1.
![]() 2.
2.
![]() 3.
3.
![]()
4.
![]() 5.
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]() 9.
9.
![]()
10.
![]() 11.
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]() 15.
15.
![]()
Доказать, что
функция
![]() является нечетной.
Решение.
Подставляем -х вместо х в выражение
для f(x):
является нечетной.
Решение.
Подставляем -х вместо х в выражение
для f(x):
4.
![]() 5.
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]() 9.
9.
![]()
10.
![]() 11.
11.
![]() 12.
12.
![]()
20. Приведите
примеры функций, имеющих следующие
периоды: 1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]()
21. Найти период
функции
![]()
Решение.
Функция
![]() имеет период
имеет период
![]() ,
функция
,
функция
![]() –
период
–
период
![]() ,
функция
,
функция
![]() –
период
–
период
![]() .
В соответсвии со свойством 2 периодических
функций наша функция является периодической
с периодом
.
В соответсвии со свойством 2 периодических
функций наша функция является периодической
с периодом
![]() ,
т.к. отрезки
,
,
–
соизмеримы. Действительно,
,
т.к. отрезки
,
,
–
соизмеримы. Действительно,
![]() .
.
Доказать, что функция
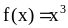 строго возрасает на множестве R.
строго возрасает на множестве R.
Решение.
Пусть
![]() –
произвольные числа, причем
–
произвольные числа, причем
![]() .
Покажем, что
.
Покажем, что
![]() .
Для этого рассмотрим разность
.
Для этого рассмотрим разность
![]()
![]() т.к. все сомножители в правой части
положительны.
т.к. все сомножители в правой части
положительны.
Докажите, что указанные ниже функции являются строго монотонными на указанных промежутках:
1.
![]() 2.
2.
![]() 3.
3.
![]()
4.
![]() 5.
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]() 9.
9.
![]()
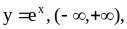 11.
11.
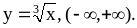
24. Найти промежутки монотонности функций:
1.
![]() 2.
2.
![]() 3.
3.
![]()
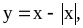 5.
5.
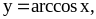 6.
6.
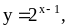
7.
![]() 8.
8.
![]()
Являются ли кусочно-монотонными следующие функции:
1.
![]() 2.
2.
![]() 3.
3.
![]()
4.
![]() 5.
5.
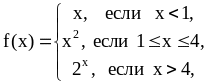
6.
![]() 7.
7.
![]() 8.
8.
![]()
25.Являются ли кусочно-монотонными следующие функции:
1. 2. 3.
4. 5.
6. 7. 8.
В математике следует помнить не формулы, а процессы мышления.
В.П. Ермаков
