1.. Векторы. Геометрическое представление вектора. Линейные операции над векторами (сложение (правило треугольников, параллелограмма, многоугольников), вычитание и умножение на действительное число), их свойства.

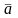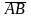Вектор − это направленный отрезок. Векторы обозначаются или , где 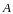− начало вектора, 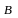− его конец. Длина вектора называется его модулем и обозначается 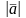или .

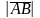Коллинеарные векторы − это векторы, направления которых совпадают или противоположны, что обозначают ׀׀ .

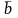Компланарные векторы − это векторы, лежащие в параллельных плоскостях, в частности, в одной плоскости.

Два вектора и называются равными, если они имеют одинаковую длину и одинаково направлены. Обозначают .

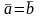Рассмотрим линейные операции над векторами.

Суммой векторов и называется вектор, идущий из начала вектора в конец вектора при условии, что начало вектора совпадает с концом вектора .

Это правило называют правилом треугольника (рис. 2.1, а) или параллелограмма (рис. 2.1, б) сложения векторов.

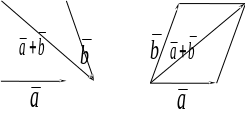
а) б)

Рис. 2.1 Сложение векторов

по правилу треугольника (а) и параллелограмма (б)

Понятие суммы векторов позволяют ввести:

1) операцию, обратную операции сложения, − разность векторов и как вектор 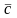такой, который в сумме с вектором дает вектор (рис. 2.2, а),

2) сложение произвольного конечного числа векторов 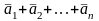(правило многоугольника) (рис. 2.2, б).

а) б)

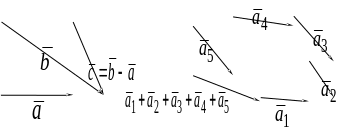
Рис.2.2 Вычитание векторов (а) и

сложение векторов по правилу многоугольника (б)

Произведением вектора на число λ называется такой вектор , который удовлетворяет условиям:

а) ;

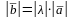б) векторы и − сонаправленные, если число λ > 0, и противоположно направленные, если λ < 0.

Таким образом, из определения операции умножения вектора на число следует, что векторы и = λ или сонаправленные или противоположно направленные, т.е. коллинеарные.

2.. Линейная зависимость векторов. Геометрический смысл линейной зависимости двух и трех векторов.

Вектор называется линейной комбинацией векторов 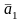, ,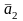…, , 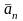если он получен из этих векторов проведением над ними линейных операций его можно представить в ви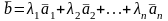де , где 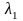, ,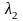…, 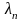− некоторые числа. Это равенство называют также разложением вектора по векторам , ,…, .

Векторы , ,…, являются линейно зависимыми, если хотя бы один из них является линейной комбинацией остальных. Например, 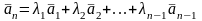. В противном случае (т.е. ни один из векторов , ,…, не может быть представлен в виде линейной комбинации остальных) векторы являются линейно независимыми.

Пара векторов на плоскости является линейно зависимой тогда и только тогда, когда эти векторы коллинеарные.

Тройка векторов в пространстве является линейно зависимой тогда и только тогда, когда эти векторы компланарны.

Необходимое и достаточное условие коллинеарности векторов

Для того что бы 2 не нулевых вектора были колинеларны необходимо и достаточно что бы они были линейно зависимы.

Необходимость:

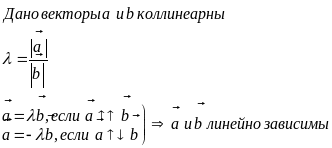
Достаточность:

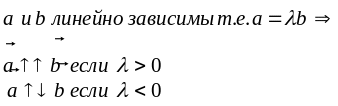
Необходимое и достаточное условие компланарности векторов:

Для того что бы 3 не нулевых вектора были компланарными необходимо и достаточно что бы они были линейно зависимы.

Необходимость: дано: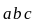

Очевидно если хотя бы пара из них колинеарны, следовательно они компланарны т.е. линейно зависимы

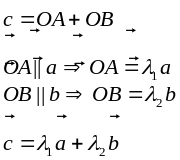
Достаточность:

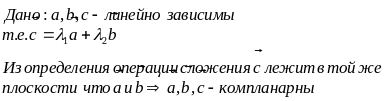
3, 4.. Базис на плоскости. Координаты вектора в данном базисе. Теорема о разложении вектора в данном базисе. Базис в пространстве.

Базисом на плоскости называется упорядоченная пара линейно независимых (т.е. неколлинеарных) векторов. Упорядоченная пара векторов означает, что указано, какой из этих векторов является первым, а какой вторым.

Любой вектор на плоскости может быть представлен как линейная комбинация базисных векторов и притом в единственном числе.

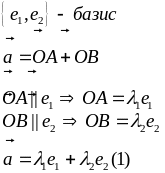
Выражение называется разложением вектора 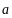по базису 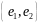. Докажем что это выражение единственное (методом от противного)

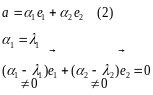
Согласно 2 определению линейной зависимости вектор 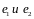линейно зависисмы т.е. колинеарны, а это невозможно т.к. они базисные, следовательно предположение о втором разложении не верно.

Замечание: коэффициенты 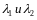называют координатами вектора в данном базисе.

Базисом в пространстве называется упорядоченная тройка линейно независимых (т.е. некомпланарных) векторов.

Каждый вектор может быть представлен как линейная комбинация базисных векторов и притом единственным образом.

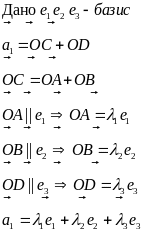
Это размножение так же единственно, доказывается аналогично R²

Например, 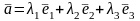. Здесь 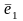, , 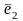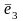− базисные векторы. Коэффициенты , , 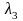разложения вектора по базисным векторам называются координатами вектора в этом базисе.

В трехмерном пространстве широко применяется декартова (прямоугольная) система координат Oxyz с базисными векторами 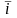, , 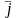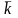. Эти векторы ортогональны (т.е. взаимно перпендикулярны) и нормированы (т.е. имеют длину равную 1). Базис , , поэтому называется ортонормированным. Любой вектор в декартовой системе координат может быть единственным образом представлен в виде .

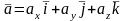Особенность декартовой системы координат в том, что коэффициенты этого разложения 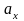, , 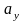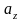(т.е. координаты вектора) являются проекциями вектора на соответствующие оси Ox, Oy и Oz.